Short-term metro passenger flow prediction based on EMD-LSTM
-
摘要: 为降低样本噪声对客流预测模型的干扰, 结合深度学习理论, 提出了一种基于经验模态分解与长短时记忆神经网络的短时地铁客流预测模型; 将预测过程分为3个阶段, 第1阶段预处理原始地铁刷卡数据, 构建进(出)站客流时间序列, 运用经验模态分解法将时间序列转化为一系列本征模函数及残差, 第2阶段利用偏自相关函数确定长短时记忆神经网络的输入变量, 第3阶段基于深度学习库Keras, 完成长短时记忆神经网络的搭建、训练及预测; 以上海地铁2号线人民广场站客流数据验证了模型的有效性。计算结果表明: 与代表性的预测模型(差分自回归移动平均模型、支持向量机、经验模态分解与反向传播神经网络、长短时记忆神经网络)相比, 经验模态分解与长短时记忆神经网络预测模型分别将工作日高峰、平峰、全日的进(出)站客流预测精度分别至少提升了2.1%(2.5%)、2.7%(3.5%)、2.7%(3.4%), 将非工作日全日的进(出)站客流预测精度至少提升了3.3%(3.5%), 说明经验模态分解与长短时记忆神经网络的组合是一种预测短时地铁客流的有效模型; 当预测步长由5 min逐渐增加至30 min时, 工作日高峰、平峰和全日进(出)站客流的平均绝对百分比预测误差分别由14.8%(13.9%)、16.8%(17.4%)和16.6%(17.0%)逐渐降低至7.0%(6.2%)、8.3%(7.5%)和8.1%(7.4%), 说明该方法预测误差与预测步长呈负相关。Abstract: To weaken the interference of sample noise to the prediction model of passenger flow, a short-term metro passenger flow prediction model was proposed based on the deep-learning theory, empirical mode decomposition(EMD) and long short-term memory neural network(LSTMNN). The prediction process was divided into three stages.In the first stage, the raw automatic fare collection(AFC) data were preprocessed, and the tap-in(tap-out) passenger flow time series were constructed and decomposed into a series of intrinsic mode functions(IMFs) and a residues by the EMD. In the second stage, the input variables of the LSTMNN were determined by the partial autocorrelation function(PACF). In the third stage, the LSTMNN was developed, trained and predicted through the deep learning library Keras. A case study of Shanghai People's Square Station on metro line 2 was conducted to validate the model performance. Calculation result shows that, compared to the representative prediction models(differential autoregressive integrated moving average model, support vector machine, empirical mode decomposition and back propagation neural network, and LSTMNN), the EMD-LSTM prediction model increases the weekdays' tap-in(tap-out) passenger flow prediction accuracy of peak hour, off-peak hour, and full-day by at least 2.1%(2.5%), 2.7%(3.5%), and 2.7%(3.4%), respectively, and also increases the weekends' tap-in(tap-out) passenger flow prediction accuracy of full-day by at least 3.3%(3.5%). Thus, the EMD-LSTM is effective to predict the short-term metro passenger flow. When the forecasting step gradually increases from 5 minutes to 30 minutes, the weekdays' tap-in(tap-out)average absolute percentage prediction errors of peak hour, off-peak hour, and full-day gradually decreases from 14.8%(13.9%), 16.8%(17.4%), and 16.6%(17.0%) to 7.0%(6.2%), 8.3%(7.5%), and 8.1%(7.4%), respectively. Therefore, the forecasting error of EMD-LSTM is negatively correlated with the forecasting step length.
-
0. 引言
4D航迹运行是针对未来小间隔、高密度空域的有效策略, 美国下一代航空运输系统和欧盟单一天空计划均将基于4D航迹的运行作为核心机制。然而即使在飞行前为每架航空器配备无冲突4D航迹, 在实际飞行过程中难免会因气象条件的改变或者其他一些紧急状况的出现而导致航空器无法准确按照飞行前配备的无冲突4D航迹飞行, 因此, 必须对空域中的实时交通态势进行监控和冲突探测, 在线计算避免飞行冲突的最优解脱策略, 从而保证空中交通的安全和畅通。
国内外学者针对飞行冲突解脱问题进行了大量的研究。首先, 从航迹解脱的决策主体来分, 冲突解脱可分为集中式冲突解脱与分布式冲突解脱。前者主要从空管自动化系统的角度为多架航空器解脱冲突[1], 而后者则是从航空器自身的角度解脱冲突[2-3]。其次, 从航迹解脱变量的限制来分, 航迹优化可分为自由飞行条件的航迹优化和航路飞行条件的航迹优化。前者在优化过程中仅考虑航空器的性能约束, 无需考虑空域、航路约束[4-6], 而后者需考虑这两方面的约束[7-8]。再次, 从优化模型和方法上划分, 优化方法可分为离散优化方法、连续优化方法和混合优化方法。离散优化方法将解脱的过程按等时间或等距离划分, 然后对各段进行优化以达到总体优化[9-10], 连续优化方法直接利用优化控制理论设计出航空器避让的最优飞行航迹[11-12], 而混合优化方法需要从离散的解脱策略和连续的解脱变量两方面同时进行优化[13-16]。最后, 从解脱优化的过程来分, 优化可分为离线静态优化和在线动态优化。前者仅根据探测到冲突时的状态给出固定的可行解脱策略[17], 而后者需要不断根据航空器运行状态与不同的优化目标实时计算解脱策略直至冲突解脱结束为止[18]。在将来较长的一段时期内空中交通管理仍然采用以地面为中心的集中管制方式, 只允许航空器在规定的航路上运行, 对航空器位置采用雷达或自动相关监视等离散采样机制, 因此, 研究集中式固定航路条件下的离散在线动态冲突解脱符合未来的发展方向。
在离散在线动态最优冲突解脱问题研究方面有不少成果。Bousson提出了基于模型预测控制的飞行冲突解脱方法, 为每一航空器在线计算速度和航向, 并生成沿着预定航路点的无冲突航迹[19]; Roussos等采用模型预测控制和分散导航函数研究了在随机风场条件下的多航空器冲突控制问题[20]; Chaloulos等提出了空中交通管理中的一种层次控制结构, 在分布式的航空器飞行管理系统之上, 在上层采用模型预测控制结合航空器动力学约束实现中期的冲突解脱[21]。但上述研究均假设风场基于快速更新周期的标称气象数据预报值, 并假设风场误差服从给定随机分布, 并未考虑计算解脱策略时实际风场的变化。风场不确定性在很大程度上影响飞行冲突探测与解脱的性能, Mondoloni给出了风场预测的不确定性统计模型, 并分析了其对航空器航迹预测精度的影响[22]; Chaloulos等描述了实际风场与风场预报之间误差的修正模型, 并仿真分析了误差修正对冲突概率的影响[23]; Delahaye等提出当航空器真空速已知条件下, 采用卡尔曼滤波方法利用雷达航迹对风矢量进行实时估计[24], 但该方法要求待估计区域存在多架航空器雷达航迹或单架航空器航迹必须存在转弯。
综上所述, 对实时风矢量进行估计成为在线动态最优冲突解脱研究需要解决的关键问题。本文在研究无扰动条件静态单一冲突解脱策略的基础上, 探讨了基于滚动时域优化的动态混合最优解脱方法, 特别针对当风矢量预测存在误差时出现模型失配而导致无法解脱的问题, 采用一种基于在线辨识方法对风矢量进行辨识, 以提高冲突解脱的动态适应性。
1. 不考虑风场的静态飞行冲突解脱
1.1 航空器飞行冲突探测模型
由于主要研究航空器冲突问题, 可以将航空器近似为质点, 忽略其姿态, 设其真空速为v1, 地速为v2, 航向角为φ, 航迹角为θ, 在偏流角较小的条件下φ≈θ, 则其在地面惯性参考坐标系中的运动学方程为
式中:
假设航空器a的初始状态为za0=(xa, ya, φa)T, 地速矢量为
式中: zr、φr分别为航空器b相对于航空器a的位置与航向角。
设航空器最小水平间隔为dmin, 差值Δ为
在同一高度层当Δ > 0时2架航空器之间当前不存在飞行冲突, 否则存在飞行冲突。
为便于根据航空器当前状态判断航空器之间未来的冲突趋势, 可以采用相对运动法。2架航空器潜在飞行冲突的探测见图 1, 每架航空器的保护区半径均为dmin/2, 2条与航空器b的保护区边缘相切并且平行于
当航空器b的飞行走廊边缘线与航空器a的飞行方向的夹角大于β+δ或者小于β-δ时, 航空器a的保护区与航空器b的飞行走廊就不会有交集, 即不存在潜在的飞行冲突, 因此, 避免飞行冲突发生的条件为
1.2 静态飞行冲突解脱策略
首先考虑2架航空器在固定航路飞行条件下, 整个冲突解脱过程中地速保持不变, 仅通过调整航空器b的航向角来进行冲突解脱。
图 2为航空器b通过调整航向角解脱冲突的航迹, 上下2条虚线L1、L2为规定的航路边界, 设在地面惯性参考坐标系中航路中心为L0, 对应的直线方程为lbzb=cb, lb为方程的系数向量, zb为航空器b的位置, cb为方程的常数项, 航路宽度为2W。当航空器b运行到P点时, 开始执行解脱程序, 此时α为
式中: Δφb为航空器b的航向角调整量。
航空器b到达Q点之后以相反的航向角调整量-Δφb回到航路中心线上飞行, 假设Q点距离航路中心线的距离为dQ, 因此, 有
图 2 航空器 b 通过调整航向角解脱冲突的航迹Figure 2. Flight path of aircraft b by adjusting course angle to resolve conflict式中: αQ、βQ分别为航空器b位于Q点时2架航空器相对速度矢量、相对位置矢量与航空器a运动方向的夹角; δQ为航空器b位于Q点时2架航空器的保护区边缘内公切线与2架航空器连线之间的夹角。
当航空器b运动至R点时航向回归φb, 若2架航空器之间的相对位置矢量与相对速度矢量内积大于零, 说明航空器的相对运动将继续增大其间隔, 若此时2架航空器的飞行保护区没有重叠, 表明飞行冲突解脱结束, 因此, 对冲突解脱结束R点的约束为
式中: zR为航空器b位于R点时的位置矢量。
忽略航空器b调整航向角所花费的时间, 冲突解脱过程所消耗的时间γ1为
从式(4)看出还可以通过调整航空器b的飞行地速来解脱冲突。假设2架航空器在整个冲突解脱过程中航向保持不变, 定义航空器b的地速调整量为Δvb, 此时有
避免飞行冲突发生的条件仍然为式(6)。航空器b的地速调整量必须在航空器性能许可的范围内, vb+Δvb∈[vmin, b, vmax, b], vmin, b、vmax, b分别为航空器b地速的最小值、最大值。
图 3为航空器b通过调整地速解脱冲突的航迹, 假设航空器b从P点开始执行解脱程序, 在到达Q点之后以相反的地速调整量-Δvb回归其原始速度, P点与R点之间的距离为σR。当航空器b运动至R点时地速回归vb, 冲突解脱结束点R点的约束仍为式(9)。
图 3 航空器 b 通过调整地速解脱冲突的航迹Figure 3. Flight path of aircraft b by adjusting ground speed to resolve conflict设航空器b的加速度为ab, 航空器b调整地速所花费的时间为2Δvb/ab, 再加上保持地速为vb+Δvb的时间, 可得解脱所消耗的总时间γ2为
根据已知的航空器初始位置和性能限制, 可以求出冲突解脱时间最短情况下航空器b的航向角调整量Δφb和地速调整量Δvb。
2. 考虑随机风场的动态飞行冲突解脱
2.1 飞行冲突解脱滚动时域优化
在实际飞行冲突解脱过程中, 可能遇到一些突发状况或者受到其他意外因素的影响, 如风矢量变化、航空器a地速发生扰动等, 显然仅仅通过静态解脱策略无法满足完全避免冲突的要求。滚动时域控制是一种基于有限时域的滚动优化控制, 在满足输入和状态限制约束的基本条件下, 通过预测模型对被控对象的未来响应以及状态进行预测, 并在有限时域内进行滚动优化[21]。
假设冲突解脱策略滚动优化的周期为A, 在整个冲突解脱过程中航空器b可同时采取调整航向角和地速的策略, 解脱区域在同一个飞行高度平面内且该水平面内风矢量未知, 因此, 需要考虑可能存在的偏流。由于对航空器的观测是基于地面一、二次雷达或ADS-B的离散采样, 因此, 航空器运动学方程可用离散状态模型描述。在地面惯性坐标系中, 同一时刻允许航迹角调整量Δθb和地速调整量Δvb同时不为零, 航空器解脱过程的航迹见图 4。
图 4 航空器 b 通过滚动时域优化解脱冲突的航迹Figure 4. Flight path of aircraft b by using receding horizon optimization在某一个滚动周期的开始时刻, 航空器b可能处于偏离航路中心方向的位置P1, 即Δθb(k)Δθb(0) > 0, Δθb(k)为第k个滚动周期内航空器b的航迹角调整量, 此时冲突解脱过程消耗的时间γ3为
若航空器b处于回归航路中心方向的位置P2, 即Δθb(k)Δθb(0)≤0, 此时冲突解脱过程消耗的时间γ4为
将上述目标综合后转化为离散形式, 在一个滚动周期内, 最优解脱问题函数J与约束分别为
式中: vb(0)为初始时刻航空器b的地速; Δvb(k)为第k个滚动周期内航空器b的地速调整量; za(k)、zb(k)分别为第k个滚动周期内航空器a、b的位置矢量; zr(k)为第k个滚动周期内航空器b相对于航空器a的位置矢量。
式(16)中, 前2个公式为航空器运动学方程约束, 第3个公式为航路边界约束, 第4个公式为航空器间隔约束。可以采用内点障碍函数法求解含有这些约束的非线性优化问题, 通过构建障碍函数把约束问题转化为无约束最优化问题, 构造的障碍函数G为
式中: κ1、κ2为大于零的常数; H1、H2分别为航路边界与航空器间隔约束函数。
障碍函数关于Δvb(k)、Δθb(k)的下降梯度函数
采用梯度下降法, 即可求解在第k个滚动周期内的混合最优解脱策略。
2.2 基于地面观测的风矢量辨识
在滚动优化模型中风矢量为预设的初值, 当风矢量存在误差的情况下可能导致在执行地面解脱策略时无法实现解脱。假设地面观测的采样周期为Δτ, 通过采集解脱之前N个采样周期内的航空器实际状态向量, 利用极大似然估计和牛顿-拉夫逊迭代算法对风矢量进行在线辨识。
令t时刻航空器b的地速˙zbt为状态向量, zbt为观测向量, Zb(k)=(xb(k), yb(k))T为测量向量, ub(t)=(vb′(t), φb(t))T为输入向量, w=(w1, w2)T为待辨识风矢量, xb(k)、yb(k)分别为第k个滚动周期内航空器b的横向、纵向位置, vb′(t)、φb(t)分别为航空器b的真空速、航向角, w1、w2分别为待辨识风矢量的横向、纵向分量。状态方程、观测方程分别为
将观测方程对待辨识风矢量求导, 可得灵敏度方程为
极大似然估计的指标函数K(w)为[25]
式中: R为航空器b的位置测量误差协方差矩阵; Zb, i、zb, i分别为第i个采样周期内关于航空器b的测量向量与观测向量。
以R为变量, 函数K(w)取极小值时, 可得R为
风矢量w的极大似然估计就是寻找估计值
式中: wk、K(wk)分别为第k个滚动周期内的风矢量与对应的指标函数; ε为迭代收敛条件参数。
2.3 最优冲突解脱策略解算
得到风矢量的极大似然估计
式中: vb′*(k)、φb*(k)分别为第k个滚动周期内航空器b的真空速、航向角的最优值; ωb(k)为第k个滚动周期内航空器b的航向角、航迹角的最优值之差。
由此得到第k个滚动周期内航空器b的真空速和航向角分别为
这样地面惯性参考坐标系下的最优混合解脱策略(Δvb*(k), Δθb*(k))T转换为航空器的操纵输入(vb′*(k), φb*(k))T。
3. 案例研究
为了验证所提方法的有效性, 对比仿真了3种情况: 无扰动下的静态解脱策略、某一航空器地速变化条件下的滚动时域优化策略以及风矢量变化条件下的滚动时域优化策略。
2架航空器在惯性坐标系内的初始位置关系见图 6。假设某管制区内有航空器a和航空器b两架航空器, 它们在同一飞行高度飞行, 高度为6km, 航空器a的初始位置为(0, 18km), 航向角为45°, 地速为720km·h-1; 航空器b的初始位置为(24km, 0), 航向角为90°, 地速为690km·h-1, 由图 6可以看出2架航空器是在逐渐接近的。
图 6 两架航空器在惯性坐标系内的初始位置关系Figure 6. Initial position relation of two aircrafts in inertial coordinate system根据民航空中交通管理规则, 设最小安全间隔设为10km, 航路宽度为16km, 其中心线两侧宽度各为8km。此外, 航空器允许加速度范围为-0.6~0.6m·s-2, 允许调速范围为-80~80km·h-1, 偏航解脱时的允许偏航角范围为-30°~30°。
3.1 静态飞行冲突解脱策略验证
假设风矢量和航空器a的地速均不发生变化, 当前航空器b与航空器a之间的距离为30km, 有
可知|α-β| < δ, 说明存在潜在冲突风险。
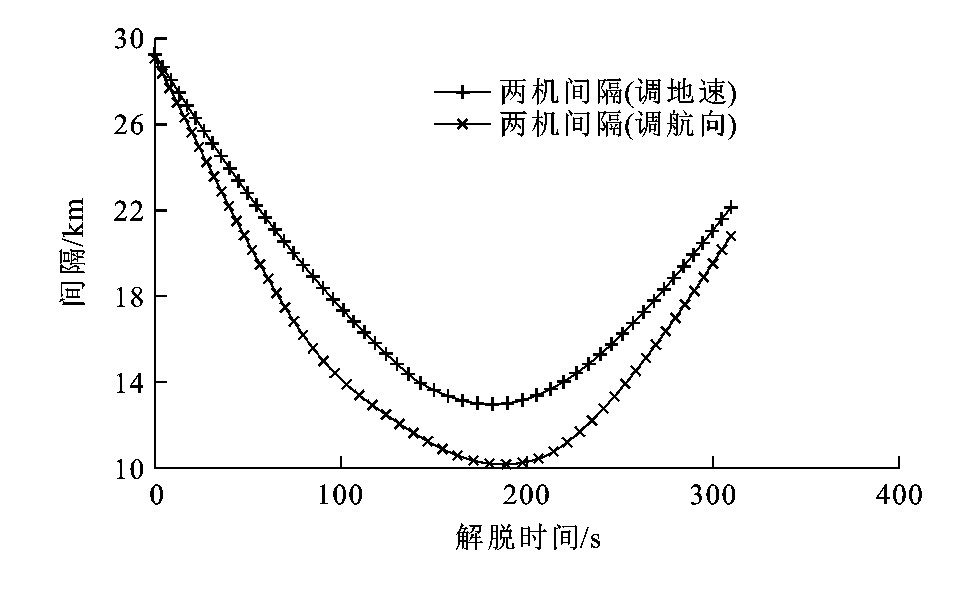
首先通过调整航空器航向角进行冲突解脱, 采用内点障碍函数法可以得到当Δφb为14.6°、dQ为4.68km时, 最短解脱时间γ1为195s。其次通过调整航空器地速进行冲突解脱, 可以得到当Δvb为-80km·h-1、σR为49.464km时, 最短解脱时间γ2为285s。图 7、8分别为解脱过程中2架航空器的轨迹曲线和2架航空器之间间隔的变化曲线。可以看出: 相对于调地速, 通过调航向能够更快地对冲突情况进行有效解脱。
图 7 解脱过程中2架航空器的轨迹曲线Figure 7. Trajectory curves of two aircrafts in resolution process
图 8 静态单一解脱策略下2架航空器之间间隔的变化曲线Figure 8. Variation curves of interval between two aircrafts under static single resolution strategy3.2 动态飞行冲突解脱策略验证
仍然假设风矢量保持不变, 在第30s时, 航空器a的地速开始发生变化, 分别假设以-0.6m·s-2的加速度减速至640km·h-1和以0.6m·s-2的加速度加速至800km·h-1。仍采用静态解脱策略时2架航空器之间间隔的变化曲线见图 9。可以看出: 当航空器a减速时, 若航空器b仍采取静态解脱策略, 2架航空器之间间隔无法满足最小间隔要求。
图 9 航空器 a 地速变化时静态解脱策略下2架航空器之间间隔的变化曲线Figure 9. Variation curves of interval between two aircrafts under static resolution strategy with changing ground speed of aircraft a假设采用基于滚动时域优化的动态解脱策略, 假设滚动周期A为5s, 取κ1=κ2=10-5。图 10、11分别为采用动态解脱策略时航空器b的轨迹曲线和2架航空器之间间隔的变化曲线。可以看出: 当航空器a地速无变化时, 需要215s可解脱冲突; 当航空器a以-0.6m·s-2的加速度减速至640km·h-1时, 解脱时间增加为240s;而当航空器a以0.6m·s-2的加速度加速至800km·h-1时, 解脱时间降低为150s。
图 10 解脱过程中航空器 b 的轨迹曲线Figure 10. Trajectory curves of aircraft b in resolution process
图 11 滚动时域优化策略下2架航空器之间间隔的变化曲线Figure 11. Variation curves of interval between two aircrafts under receding horizon optimization strategy与静态飞行冲突解脱策略相比, 当航空器a地速发生变化时, 通过调整航空器b的航向角和地速能够及时应对变化, 反映了动态滚动时域优化策略较静态策略具有较好的动态适应性。
3.3 风矢量辨识与冲突解脱验证
进一步假设坐标原点处风矢量的估计
将风场数据加载至航空器运动学模型中, 并对解脱过程中2架航空器的轨迹进行仿真。取航空器状态采样周期Δτ为1s, 并记录航空器b的操纵输入样本和地面轨迹观测样本, 每次计算最优滚动策略时样本数量取为20。采用牛顿-拉夫逊迭代算法, 取ε=0.001, 在线求解得到随机风场风分量与实际风场风分量的差值即误差见图 13, 其中w1的平均绝对误差为0.049km·h-1, 相对误差为0.173%, w2的平均绝对误差为-0.067km·h-1, 相对误差为-0.205%。
图 13 随机风场风分量与实际风场风分量的差值Figure 13. Differences between wind components of random wind field and actual wind field为对比风矢量辨识前后对滚动时域优化模型的影响, 首先不对风矢量进行辨识, 将滚动时域优化解脱策略给出的地速和航迹角直接作为航空器b的输入, 然后利用式(28)求解真空速和航向角并将它们作为航空器b的输入。图 14、15分别为风矢量辨识前后解脱过程中2架航空器的轨迹曲线和2架航空器之间间隔的变化曲线。
图 14 风矢量辨识前后航空器 b 的轨迹曲线Figure 14. Trajectory curves of aircraft b before and after wind vector identification
图 15 风矢量辨识前后2架航空器之间间隔的变化曲线Figure 15. Variation curves of interval between two aircrafts before and after wind vector identification可以看出, 在风矢量辨识前需要经过215s可解脱冲突, 当对风矢量进行辨识后解脱时间减少为160s, 总解脱时间较直接将地速作为航空器b的输入时的解脱时间大大缩短。当风矢量发生变化时, 通过在线风矢量辨识, 使得航空器b的航向角和真空速能够及时应对变化, 反映了基于风矢量辨识的动态最优解脱策略具有较好的动态适应性。
4. 结语
(1) 基于固定航路的2架航空器的冲突解脱问题, 在调航向角和调地速的单一最优解脱策略的基础上, 考虑到航空器飞行过程中的一些不确定因素, 给出了一种基于滚动时域优化的动态混合最优解脱策略, 特别针对当风矢量预测存在误差时出现模型失配而导致无法解脱的问题, 采用牛顿-拉夫逊迭代算法对风矢量进行在线辨识。
(2) 通过对无扰动下的静态优化、某一航空器地速变化条件下的滚动时域优化以及风矢量不为零但未知条件下的滚动时域优化的解脱策略的对比发现, 基于风矢量辨识的滚动时域优化方法能够应对在实际飞行冲突过程中可能出现的风矢量、航空器地速突然变化的情况, 使得动态混合最优解脱策略能够及时应对变化, 具有较好的动态适应性。
(3) 未来的研究将侧重在基于滚动时域优化的三维空间中的多机飞行冲突解脱方法。
-
图 3 日进站客流序列EMD分解结果
Figure 3. EMD decomposition results of daily tap-in passenger flow sequence
图 4 本征模函数分量和残差的偏自相关系数
Figure 4. Partial autocorrelation coefficients of IMFs and residue
表 1 预测误差对比
Table 1. Comparison of prediction errors
客流类型 模型 工作日 非工作日 高峰 平峰 全日 全日 E1/% E2 E1/% E2 E1/% E2 E1/% E2 进站 ARIMA 15.23 695 17.17 237 16.93 308 18.43 320 SVM 14.21 642 16.40 205 16.13 274 17.62 298 LSTM 12.41 540 15.39 189 15.03 264 16.05 271 EMD-BPNN 10.75 473 13.49 175 13.16 248 14.56 254 EMD-LSTM 8.62 368 10.75 161 10.49 211 11.23 198 出站 ARIMA 14.61 728 16.92 251 16.64 302 17.68 310 SVM 13.29 690 16.49 220 16.10 298 17.60 308 LSTM 11.92 659 15.54 204 15.10 291 16.39 289 EMD-BPNN 9.76 562 13.07 164 12.67 246 14.62 261 EMD-LSTM 7.31 421 9.56 117 9.29 175 11.08 178 
下载: 导出CSV
-
[1] 蔡昌俊, 姚恩建, 王梅英, 等. 基于乘积ARIMA模型的城市轨道交通进出站客流量预测[J]. 北京交通大学学报, 2014, 38(2): 135-140. https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT201402024.htmCAI Chang-jun, YAO En-jian, WANG Mei-ying, et al. Prediction of urban railway station's entrance and exit passenger flow based on multiply ARIMA model[J]. Journal of Beijing Jiaotong University, 2014, 38(2): 135-140. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT201402024.htm [2] 袁坚, 王鹏, 王钺, 等. 基于时空特征的城市轨道交通客流量预测方法[J]. 北京交通大学学报, 2017, 41(6): 42-48. https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT201706009.htmYUAN Jian, WANG Peng, WANG Yue, et al. A passenger volume prediction method based on temporal and spatial characteristics for urban rail transit[J]. Journal of Beijing Jiaotong University, 2017, 41(6): 42-48. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT201706009.htm [3] 杨军, 侯忠生. 一种基于灰色马尔科夫的大客流实时预测模型[J]. 北京交通大学学报, 2013, 37(2): 119-123, 128. doi: 10.3969/j.issn.1673-0291.2013.02.022YANG Jun, HOU Zhong-sheng. A grey Markov based on large passenger flow real-time prediction model[J]. Journal of Beijing Jiaotong University, 2013, 37(2): 119-123, 128. (in Chinese). doi: 10.3969/j.issn.1673-0291.2013.02.022 [4] 王兴川, 姚恩建, 刘莎莎. 基于AFC数据的大型活动期间城市轨道交通客流预测[J]. 北京交通大学学报, 2018, 42(1): 87-93. https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT201801013.htmWANG Xing-chuan, YAO En-jian, LIU Sha-sha. Urban rail transit passenger flow forecasting for large special event based on AFC data[J]. Journal of Beijing Jiaotong University, 2018, 42(1): 87-93. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT201801013.htm [5] 姚恩建, 周文华, 张永生. 城市轨道交通新站开通初期实时进出站客流量预测[J]. 中国铁道科学, 2018, 39(2): 119-127. doi: 10.3969/j.issn.1001-4632.2018.02.15YAO En-jian, ZHOU Wen-hua, ZHANG Yong-sheng. Real-time forecast of entrance and exit passenger flow for newly opened of urban rail transit at initial stage[J]. China Railway Science, 2018, 39(2): 119-127. (in Chinese). doi: 10.3969/j.issn.1001-4632.2018.02.15 [6] LI Yang, WANG Xu-dong, SUN Shuo, et al. Forecasting short-term subway passenger flow under special events scenarios using multiscale radial basis function networks[J]. Transportation Research Part C: Emerging Technologies, 2017, 77: 306-328. doi: 10.1016/j.trc.2017.02.005 [7] SUN Yu-xing, LENG Biao, GUAN Wei. A novel wavelet-SVM short-time passenger flow prediction in Beijing subway system[J]. Neurocomputing, 2015, 166: 109-121. doi: 10.1016/j.neucom.2015.03.085 [8] 李得伟, 颜艺星, 曾险峰. 城市轨道交通进站客流量短时组合预测模型[J]. 都市快轨交通, 2017, 30(1): 54-58, 64. doi: 10.3969/j.issn.1672-6073.2017.01.012LI De-wei, YAN Yi-xing, ZENG Xian-feng. Combined short-term prediction model of station entry flow in urban rail transit[J]. Urban Rapid Rail Transit, 2017, 30(1): 54-58, 64. (in Chinese). doi: 10.3969/j.issn.1672-6073.2017.01.012 [9] 熊杰, 关伟, 孙宇星. 基于Kalman滤波的地铁换乘客流预测[J]. 北京交通大学学报, 2013, 37(3): 112-116, 121. doi: 10.3969/j.issn.1673-0291.2013.03.021XIONG Jie, GUAN Wei, SUN Yu-xing. Metro transfer passenger forecasting based on Kalman filter[J]. Journal of Beijing Jiaotong University, 2013, 37(3): 112-116, 121. (in Chinese). doi: 10.3969/j.issn.1673-0291.2013.03.021 [10] 李春晓, 李海鹰, 蒋熙, 等. 基于广义动态模糊神经网络的短时车站进站客流量预测[J]. 都市快轨交通, 2015, 28(4): 57-61. doi: 10.3969/j.issn.1672-6073.2015.04.012LI Chun-xiao, LI Hai-ying, JIANG Xi, et al. Short-term entrance passenger flow forecast at urban rail transit station based on generalized dynamic fuzzy neural networks[J]. Urban Rapid Rail Transit, 2015, 28(4): 57-61. (in Chinese). doi: 10.3969/j.issn.1672-6073.2015.04.012 [11] DING Chuan, WANG Dong-gen, MA Xiao-lei, et al. Predicting short-term subway ridership and prioritizing its influential factors using gradient boosting decision trees[J]. Sustainability, 2016, 8(11): 1-16. [12] LENG Biao, ZENG Jia-bei, XIONG Zhang, et al. Probability tree based passenger flow prediction and its application to the Beijing subway system[J]. Frontiers of Computer Science, 2013, 7(2): 195-203. doi: 10.1007/s11704-013-2057-y [13] ZHAO Zheng, CHEN Wei-hai, WU Xing-ming, et al. LSTM network: a deep learning approach for short-term traffic forecast[J]. IET Intelligent Transport Systems, 2017, 11(2): 68-75. doi: 10.1049/iet-its.2016.0208 [14] MA Xiao-lei, TAO Zhi-min, WANG Yin-hai, et al. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data[J]. Transportation Research Part C: Emerging Technologies, 2015, 54: 187-197. [15] POLSON N G, SOKOLOV V O. Deep learning for short-term traffic flow prediction[J]. Transportation Research Part C: Emerging Technologies, 2017, 79: 1-17. [16] LYU Yi-Sheng, DUAN Yan-Jie, KANG Wen-wen, et al. Traffic flow prediction with big data: a deep learning approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(2): 865-873. [17] LIU Li-juan, CHEN Rung-ching. A novel passenger flow prediction model using deep learning methods[J]. Transportation Research Part C: Emerging Technologies, 2017, 84: 74-91. [18] HUANG Wen-hao, SONG Guo-jie, HONG Hai-kun, et al. Deep architecture for traffic flow prediction: deep belief networks with multitask learning[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(5): 2191-2201. [19] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454: 903-995. [20] WEI Yu, CHEN Mu-chen. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks[J]. Transportation Research Part C: Emerging Technologies, 2012, 21(1): 148-162. [21] CHEN Syuan-yi, CHOU Wei-yao. Short-term traffic flow prediction using EMD-based recurrent Hermite neural network approach[C]∥IEEE. 15th International IEEE Conference on Intelligent Transportation Systems. New York: IEEE, 2012: 1821-1826. [22] WANG Hai-zhong, LIU Lu, DONG Shang-jia, et al. A novel work zone short-term vehicle-type specific traffic speed prediction model through the hybrid EMD-ARIMA framework[J]. Transportmetrica B: Transport Dynamics, 2016, 4(3): 159-186. [23] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. [24] ZHONG Chen, BATTY M, MANLEY E D, et al. Variability in regularity: mining temporal mobility patterns in London, Singapore and Beijing using smart-card data[J]. PloS One, 2016, 11(2): 1-17. [25] TANG Li-yang, ZHAO Yang, JAVIER C, et al. Forecasting short-term passenger flow: an empirical study on Shenzhen metro[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(10): 3613-3622. [26] AN Ning, ZHAO Wei-gang, WANG Jian-zhou, et al. Using multi-output feedforward neural network with empirical mode decomposition based signal filtering for electricity demand forecasting[J]. Energy, 2013, 49: 279-288. [27] ZHENG Hui-ting, YUAN Jia-bin, CHEN Long. Short-term load forecasting using EMD-LSTM neural networks with a Xgboost algorithm for feature importance evaluation[J]. Energies, 2017, 10(8): 1-20. [28] ZHANG Xi-ke, ZHANG Qiu-wen, ZHANG Gui, et al. A novel hybrid data-driven model for daily land surface temperature forecasting using long short-term memory neural network based on ensemble empirical mode decomposition[J]. International Journal of Environmental Research and Public Health, 2018, 15(5): 1-23. [29] CHERKSSKY V, MA Y Q. Practical selection of SVM parameters and noise estimation for SVM regression[J]. Neural Networks, 2004, 17(1): 113-126. [30] 张晚笛, 陈峰, 王子甲, 等. 基于多时间粒度的地铁出行规律相似性度量[J]. 铁道学报, 2018, 40(4): 9-17. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201804002.htmZHANG Wan-di, CHEN Feng, WANG Zi-jia, et al. Similarity measurement of metro travel rules based on multi-time granularities[J]. Journal of the China Railway Society, 2018, 40(4): 9-17. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201804002.htm -
下载:
点击查看大图
计量
- 文章访问数: 1741
- HTML全文浏览量: 448
- PDF下载量: 848
- 被引次数: 0
