Distributed cooperative predictive control of virtual coupled trains
-
摘要: 为提高虚拟编组列车的协同跟踪效率和编队的稳定性，提出了一种基于分布式模型预测控制(DMPC)的多列车交互协同跟踪控制方法，基于单元列车动力学分析建立了虚拟编组领导者-跟随者列车双向拓扑结构的状态空间模型，以改善单向拓扑结构的局限性，使得通信结构更稳固；在代价指标函数中引入邻接系统状态信息，并与自身状态信息进行加权融合，设计了改进的DMPC算法，在运行速度限制、距离限制和控制量限制等约束条件下，通过求解改进的代价指标函数得到了列车最优控制量和最优状态量，实现了虚拟编组列车的分布式协同控制，并从理论上证明了算法的可行性与闭环稳定性；采用实验室配备的列车追踪运行半实物仿真系统进行仿真，以4列CRH380A单元列车组成的虚拟编组列车为控制对象，使其跟踪设定的期望速度曲线，并与其他传统算法进行了对比。仿真结果表明：在不同初始条件下，虚拟编组列车的距离误差和速度误差均能在300 s后收敛，控制输出能满足乘客舒适性要求，且各单元列车在收到速度调整指令后仍可保持稳定编组队形；采用提出的方法得到的虚拟编组列车的速度和距离均方根误差分别为3.32×10-8 km·h-1和6.11×10-7 m，相比传统方法均降低了99.99%，可见，提出的方法的控制跟踪性能优于传统控制方法，且各单元列车的采样时刻仿真时长均能保证在3 ms内，满足高速列车控制系统的要求。Abstract: To improve the cooperative tracking efficiency and stability of virtual coupled trains, a multi-train interactive cooperative tracking control method was proposed based on the distributed model predictive control (DMPC). A state-space model of virtual coupled leader-follower trains bidirectional topology was established based on the unit train dynamics analysis, so as to improve the limitation of unidirectional topology and make the communication structure more stable. The improved DMPC algorithm was designed by introducing the neighboring system state information into the cost index function and weighting it with the self-state information. Under the constraints of running velocity limit, distance limit, and control quantity limit, the optimal control quantity and state quantity of trains were obtained by solving the improved cost index function, the distributed cooperative control of virtual coupled trains was realized, and the feasibility and closed-loop stability of the algorithm were theoretically proven. The semi-physical simulation system for train tracking and running in the laboratory was used for simulation. The virtual coupled trains consisting of four CRH380A unit trains were controlled to track a specified velocity curve and compared the proposed algorithm with other traditional algorithms. Simulation results indicate that under different initial conditions, the distance and velocity errors of virtual coupled trains can converge after 300 s, the control output can meet the requirements of passenger comfort, and each unit train can still maintain a stable coupled formation after receiving the velocity adjustment instruction. The root mean square errors of velocity and distance of virtual coupled trains obtained by the proposed method are 3.32×10-8 km·h-1 and 6.11×10-7 m, respectively, which are 99.99% lower than traditional methods. Therefore, the control and tracking performance of the proposed method is superior to that of traditional control methods, and the sampling time simulation duration of each unit train can be guaranteed within 3 ms, meeting the requirements of high-speed train control system.
-
0. 引言
为提升高速铁路运输效率和能力，基于车车通信方式连接的虚拟编组列车已成为未来列车运行控制系统的发展方向和研究热点[1]。虚拟编组列车不仅可以提升列车运行效率，而且通过灵活的动态编组和解编可以大大降低运输成本[2-3]，但由于列车实际运行环境复杂多变，平稳精准的速度跟踪和保证列车编队稳定是虚拟编组列车实现的难点。
针对以上研究问题，国内外研究学者展开了大量研究。虚拟编组这个概念首先由Bock等[4]提出，他们提出了一种新的列车运行方式，即列车之间不再需要物理车钩实现编组，而是通过某种方式虚拟编组在一起，但具体编组方式并没有指出；而后Ständer等[5]提出可以采用无线通信连接方式代替传统的物理车钩，但由于技术水平的限制，该方法并没有具体实施。近年来，随着列车自动驾驶及无线通信等技术的迅猛发展，虚拟编组已经成为当前铁路系统中的研究热点。2015年5月，欧盟全面启动了Shift2Rail(S2R)计划，详细规划了虚拟编组技术的研究方向，推动了虚拟编组研究的发展[6-7]。
作为一种基于无线通信的网联系统，虚拟编组列车针对不同的控制目标，可以设计不同的拓扑结构，不同的结构不仅影响控制器的设计，而且实现的控制效果也不同。早期网联系统的通信拓扑结构设计通常仅采用简单的单向传播方式，且只能接收来自邻近智能体的信息[8]。随着4G、5G等新兴无线通信技术的发展，各网联系统的通信拓扑方式也随之增多，就编组列车而言，常用拓扑结构包括领航跟随型、前车跟随型和领航-前车跟随型等[9]。在智能网联车队控制领域，Naus等[10]采用了前车跟随型通信拓扑结构，该拓扑结构仅接收来自前方运行车辆的状态信息，以保持与前车协同运行为控制目标，但该结构忽略了与后车之间的耦合关系，导致整体编队稳定性较差。在此基础上，有研究学者提出了双向通信拓扑结构，即增加了对后车状态信息的接收。Knorn等[11]采用双向通信拓扑方式，通过仿真试验验证了该结构可以进一步增强系统稳定性；朱旭等[12]采用了双向-领航车跟随通信拓扑结构，该拓扑结构可以加快车辆队列误差衰减并加强队列稳定性。而在虚拟编组列车编队控制领域，采用的通信拓扑方式多为单向型[13-14]，这将难以保证队列稳定性。鉴于此，本文将虚拟编组列车的通信拓扑方式设计为双向型，即每列单元列车均能接收来自前后两列车的运行状态信息，极大程度地改善了虚拟编组列车单向拓扑结构的局限性，使得通信结构更稳固，并且能够进一步增强列车协同编队控制的稳定性。
对于虚拟编组列车来说，其闭塞方式不同于传统的固定闭塞与移动闭塞，它的每个单元列车之间都以远小于列车制动距离的小间距追踪运行，通过控制前后两列车的相对制动距离避免单元列车间追尾等事故的发生。基于相对距离制动模式(Relative Distance Braking Mode, RDBM)(“撞软墙”)的安全高效跟随控制策略是虚拟编组列车安全运行的核心技术之一。张友兵等[15]在研究既有闭塞技术的基础上，提出了基于虚拟编组列车控制系统的关键技术和控制策略；宋志丹等[16]在列控系统防护方案中引入了相对制动距离的概念，并提出了一种基于相对制动距离的限速曲线计算方法；Su等[17]提出了一种基于RDBM的协同避碰控制方法，可以在保证安全的前提下提高运行效率，与绝对距离制动模式(Absolute Distance Braking Mode, ADBM)(“撞硬墙”)相比，该方法大大降低了虚拟编组列车的跟车距离；而后Su等[18]又提出了一种具有非均匀制动动力学能力的列车稳定编组方案，通过引入一种基于相对制动距离的间隔策略，设计了适用于虚拟编组列车集的线性控制结构，以保持平衡间距。
针对基于RDBM的虚拟编组列车协同编队控制问题，许多学者已开展了相关研究[19-20]。Wang等[21]采用滑模控制(Sliding Mode Control, SMC)策略，对考虑外界环境干扰作用的虚拟编组列车进行编队控制，通过设计合适的滑模面使得虚拟编组列车跟踪参考运行状态；Liu等[22]提出了一种基于二阶非线性列车动力学的终端SMC来维持耦合编队状态的方法，并通过设计非线性观测器消除了时变测量延迟引起的估计误差；Wang等[23]使用强化学习(Reinforcement Learning, RL)和人工势场对虚拟编组列车进行编队控制。由于现有轨道条件和列车性能的限制，基于RL的控制在实际列车运行过程中难以实现，并且算法稳定性得不到保证。SMC能跟踪参考点，但不能根据前行列车的未来运行状态做出相应调整。而在列车实际运行过程中，后行列车不仅要根据前行列车的未来运行状态做出调整，以保证各单元列车的安全间距，而且由于列车制动性能及轨道线路条件等因素的影响，还需保证各单元列车不能超过轨道安全限速。同时为满足乘客舒适性需求，列车控制力也应限制在一定范围内，因此，针对以上带约束条件的虚拟编组列车运行控制问题，一些研究学者采用具有显示处理约束能力的模型预测控制(Model Predictive Control, MPC)方法对虚拟编组列车进行跟踪控制。例如，Xun等[24]提出了一种基于列车动态特性的多车协同集中式模型预测控制(Centralized Model Predictive Control, CMPC)方法，以调整列车的跟车距离；Chen等[25]提出一种基于MPC的虚拟编组列车协同防撞控制方法，在不同场景下进行了仿真，仿真结果表明MPC策略在减低目标函数能量方面效果最优；Su等[26]针对具有非线性安全均衡间隔策略的虚拟编组列车集，提出了一种CMPC策略，根据列车的制动距离差和速度差，给出控制器在巡航阶段的跟踪目标；Xun等[27]提出了一种基于相对坐标极限速度差的计算方法和基于MPC的虚拟编组列车协调碰撞缓减方法。
以上大部分控制策略均采用集中式控制，但在实际列车控制系统中，采用集中式控制不仅会给控制器带来巨大负担，导致丢包、错包的概率大大增加，还会造成资源浪费及安全隐患。而采用分布式控制方法则可以较好地解决该问题，它不仅大大降低了通信成本，而且减少了列车能耗。在现有研究中，分布式控制策略已运用到各个控制领域。杨辉等[28]提出了一种基于分布式模型的动车组预测控制方法，实现了各动力单元牵引/制动力和运行速度的同步跟踪；李中奇等[29]设计了一种分布式神经网络滑模控制方法，对高速动车组进行了速度跟踪控制；赵凯辉等[30]将高速列车与多智能体系统相结合，提出了一种基于改进扰动观测器的高速列车分布式速度协同跟踪控制一致性算法。
分布式模型预测控制(Distributed Model Predictive Control, DMPC)是一种将MPC和分布式策略结合起来的控制算法，它不仅拥有MPC显示处理约束的能力，而且具备分布式控制策略的优势，如容错性强、灵活性高等。在多智能体系统控制研究中，如无人机和汽车车辆编队等，已有学者采用过DMPC算法。例如，赵超轮等[31]利用领导者-跟随者策略提出了一种基于DMPC的控制算法，实现了多架无人机队形保持飞行；陈龙等[32]针对具有状态和控制约束的非线性车辆队列系统多目标控制问题，提出了一种分布式多目标MPC策略；戴邵武等[33]设计了一种在多约束条件下的DMPC算法，使无人机在满足限制约束的条件下实现轨迹跟踪编队运行。与上述2种控制系统类似，虚拟编组列车作为一种大型多智能体系统，与无人机和汽车车辆不同的是，列车具有质量大、速度快以及不确定性大的特点，这大大增加了控制器设计的难度。基于以上分析，为改进CMPC算法在虚拟编组控制领域的缺陷，可以采用DMPC算法进一步提高系统的控制性能。而在虚拟编组列车编队控制系统设计中，DMPC算法的应用少之又少。Liu等[34]利用DMPC研究了虚拟编组列车运行控制问题，但算法中的性能指标函数并未考虑拓扑连接单元列车的状态信息，队形并不稳定。
鉴于此，本文针对虚拟编组列车跟踪控制问题，设计了一种改进性能指标函数的DMPC算法，将邻接系统与自身系统的状态信息进行加权融合，提高系统的控制性能。在模型构建方面，相比已有虚拟编组列车单向通信拓扑模型[13-14]，本文构建了虚拟编组列车双向拓扑结构的动力学模型，即在虚拟编队内的列车均可接收来自前后2列单元列车的状态信息，以双向通信方式加强了列车编队稳定性；在算法设计方面，相比已有DMPC算法[34]，提出的算法在保证列车运行安全间距、速度安全限制和控制量限制的同时，将拓扑连接的单元列车的状态信息考虑至性能指标函数中，构建了新的状态指标函数，使得列车编组运行控制效果更好；在仿真试验方面，本文采用高速列车追踪运行半实物仿真系统进行了仿真试验，验证了算法的有效性和优势。
1. 模型建立
1.1 列车动力学模型
为了实现对虚拟编组列车的速度跟踪控制，建立准确的列车动力学模型是首要前提，单个列车动力学模型为
{˙si(t)=vi(t)mi˙vi(t)=miui(t)−{r[vi(t)]+g[si(t)]}r[vi(t)]=c0+c1vi(t)+c2v2i(t) (1) 式中：$s_{i}(t)$为列车$i(i=0, 1, \cdots, I, i=0$时为领导者列车，$i=1, 2, \cdots, I$时为跟随者列车，$I$为列车总数)在$t$时刻的实际位移；$v_{i}(t)$为列车$i$在$t$时刻的实际速度；$m_{i}$为列车$i$的质量(为方便后续控制设计，假设每列列车质量相同，即均为$m) ; u_{i}(t)$为列车$i$在$t$时刻的控制输入(包括牵引加速度和制动加速度)；$r\left[v_{i}(t)\right]$为$t$时刻列车$i$受到的基本阻力；$c_{0} 、c_{1}$和$c_{2}$均为基本运行阻力系数，可根据以往经验得到；$g\left[s_{i}(t)\right]$为$t$时刻列车$i$的附加阻力，包括坡道阻力和曲线阻力，两者均与列车所在位置有关。
进一步得到列车动力学方程为
{˙si(t)=vi(t)m˙vi(t)=mui(t)−{r[vi(t)]+g[si(t)]} (2) 1.2 虚拟编组列车状态空间模型
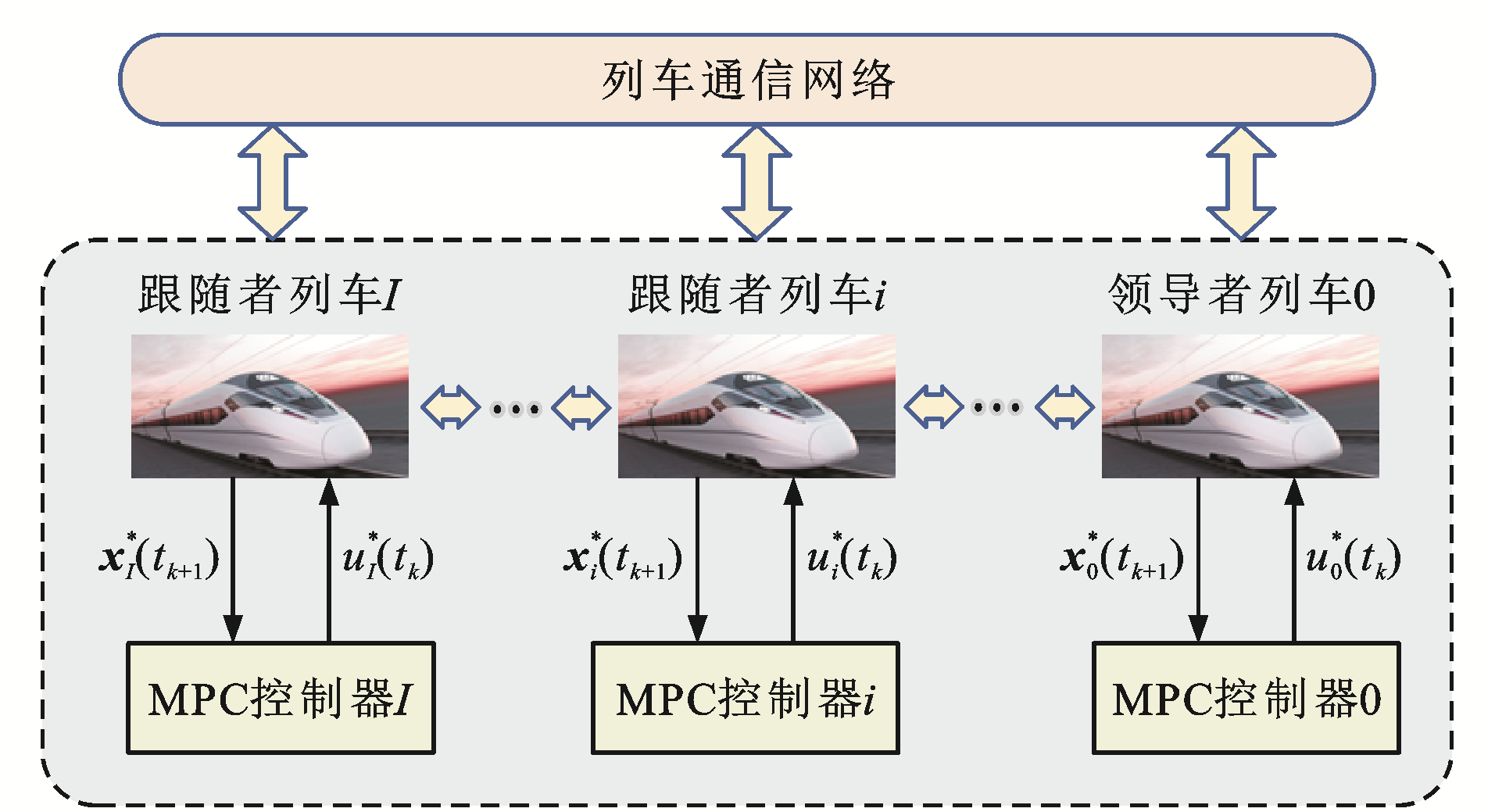
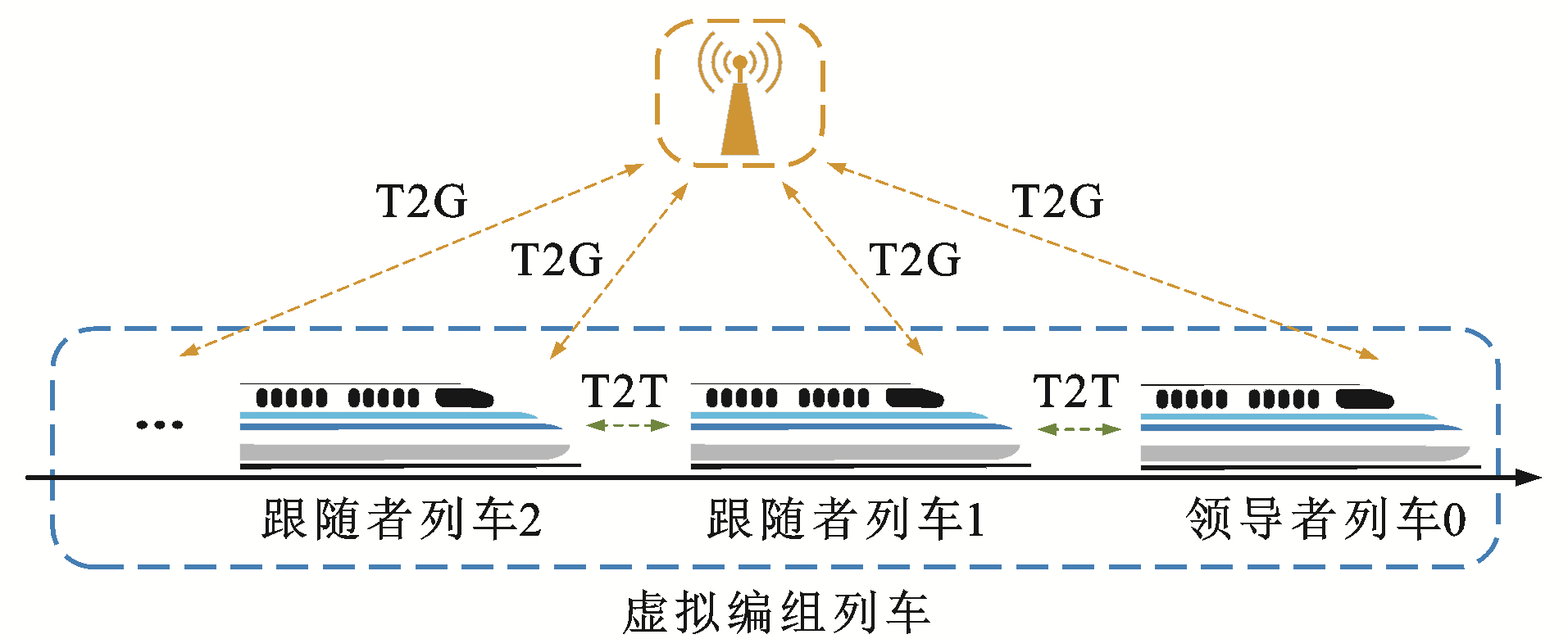
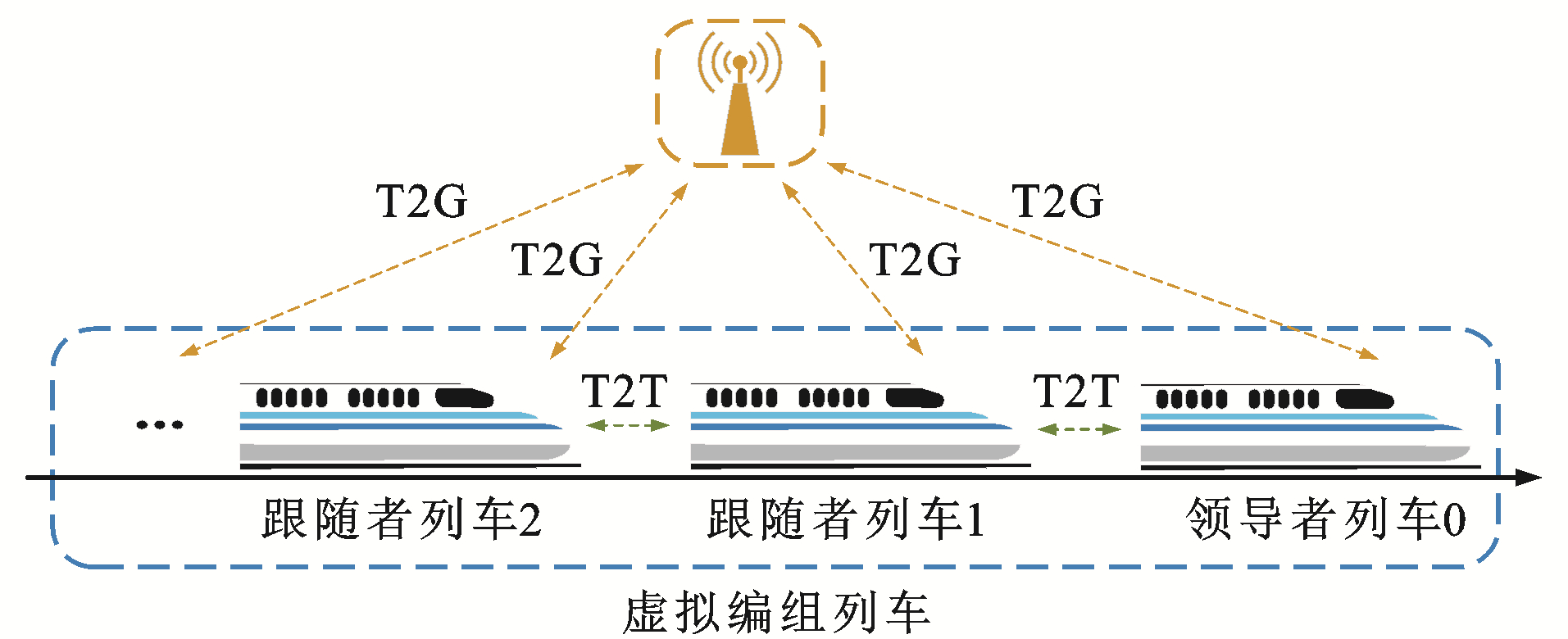
与传统物理连挂方式不同，虚拟编组各单元列车需通过车-车(Train to Train, T2T)和车-地(Train to Ground, T2G)通信2种方式进行连接，即不需要通过物理车钩的连接。图 1为本文采用的列车通信拓扑结构，通过该通信方式，每列车均可接收来自前行及后行列车上的运行信息，如位置、速度和控制量等。在实现速度跟踪控制的基础上保证本单元列车与前行和后行列车之间均有一个安全运行间隔，避免发生碰撞，这种通信方式为分布式控制系统设计提供了便利。
传统通过物理车钩进行连接的列车，其控制目标是跟踪所需的速度曲线。那些没有独立牵引和制动装置的车辆是由耦合器施加额外作用力，使其与前列列车保持近似恒定的距离。耦合器的存在可以避免列车之间的间距小于耦合器长度的限制距离，并且耦合器的作用力使得后列列车可以跟踪前列列车的运行速度。在虚拟编组列车运行控制中，列车应该像传统物理耦合列车一样组合运行，这就意味着在虚拟编组列车中领导者和跟随者的控制策略是不同的。
对于领导者列车i=0和跟随者列车i=I来说，前方不存在任何前行列车或后方不存在后行列车，就像物理耦合列车中的第一节车厢和最后一节车厢一样，第一列列车的控制目标就是跟踪所需的参考速度并保证与后行列车有一个安全距离，最后一列列车的控制目标就是跟踪前行列车速度并保证与前行列车的安全间距，因此，本文将领导者列车0及跟随者列车I的状态变量设置为
{x0(t)=(evr,0(t),ev0,1(t),0,es0,1(t))Tevr,0(t)=vr(t)−v0(t)ev0,1(t)=v0(t)−v1(t)es0,1(t)=s0(t)−s1(t)−D0,1−Li (3) {xI(t)=(evI−1,I(t),0,esI−1,I(t),0)TevI−1,I(t)=vI−1(t)−vI(t)esI−1,I(t)=sI−1(t)−sI(t)−DI−1,I−Li (4) 式中：$\boldsymbol{x}_{0}(t)$为$t$时刻领导者列车0的状态变量；$\boldsymbol{x}_{I}(t)$为$t$时刻列车$I$的状态变量；$v_{\mathrm{r}}(t)$为$t$时刻领导者列车0的跟踪参考速度；$e_{v_{\mathrm{r}, 0}}(t)$为$t$时刻领导者列车0运行速度$v_{0}(t)$与参考速度$v_{\mathrm{r}}(t)$的偏差；$e_{v_{0, 1}}(t)$为$t$时刻领导者列车0运行速度$v_{0}(t)$与跟随者列车1运行速度$v_{1}(t)$的偏差；$e_{s_{0, 1}}(t)$为$t$时刻领导者列车0实际位移$s_{0}(t)$与跟随者列车1实际位移$s_{1}(t)$减去车身长度$L_{i}$后距离与期望距离$D_{0, 1}$的偏差；$e_{v_{I-1, I}}(t)$为$t$时刻列车$I$运行速度$v_{I}(t)$与前列列车$I-1$运行速度$v_{I-1}(t)$的偏差；$e_{s_{I-1, I}}(t)$为$t$时刻列车$I$的实际位移$s_{I}(t)$与前列列车$I-1$的实际位移$s_{I-1}(t)$减去车身长度$L_{i}$后距离与期望距离$D_{I-1, I}$的偏差，本文假设每列列车长度均为$L$。
对于跟随者列车$i=1, 2, \cdots, I-1$，其控制原理也与物理耦合列车类似，在传统车钩耦合列车中，每节车廂之间均保持一定耦合器长度的距离，为了模拟物理耦合列车的运行状态，跟随者列车的控制目标为各单元列车在速度一致的情况下，列车前后还需保证一定的期望安全间距，因此，将跟随者列车的状态变量设置为
{xi(t)=(xi,1(t),xi,2(t),xi,3(t),xi,4(t))T=(evi−1,i(t),evi,i+1(t),esi−1,i(t),esi,i+1(t))Tevi−1,i(t)=vi−1(t)−vi(t)evi,i+1(t)=vi(t)−vi+1(t)esi−1,i(t)=si−1(t)−si(t)−Di−1,i−Lesi,i+1(t)=si(t)−si+1(t)−Di,i+1−L (5) 式中：$\boldsymbol{x}_{i}(t)$为$t$时刻列车$i$的状态变量；$e_{v_{i-1, i}}(t)$为$t$时刻列车$i$运行速度$v_{i}(t)$与前列列车$i-1$运行速度$v_{i-1}(t)$的偏差；$e_{s_{i-1, i}}(t)$为$t$时刻列车$i$实际位移$s_{i}(t)$与前列列车$i-1$实际位移$s_{i-1}(t)$减去车身长度$L$后距离与期望距离$D_{i-1, i}$的偏差，假设两相邻列车之间的期望距离均为$D$。
将式(2)代入式(5)得到列车i的状态方程为
{˙xi,1(t)=ui−1(t)−ui(t)−a1evi−1,i(t)+b1˙xi,2(t)=ui(t)−ui+1(t)−a2evi,i+1(t)+b2˙xi,3(t)=evi−1,i(t)˙xi,4(t)=evi,i+1(t) (6) {a1={c1+c2[vi−1(t)+vi(t)]}/ma2={c1+c2[vi+1(t)+vi(t)]}/mb1=Δg[si(t)]=g[si(t)]−g[si−1(t)]b2=Δg[si+1(t)]=g[si+1(t)]−g[si(t)] 式中: $\Delta g\left[s_{i}(t)\right]$为列车$i$的附加阻力$g\left[s_{i}(t)\right]$与列车$i-1$的附加阻力$g\left[s_{i-1}(t)\right]$之差。
由于2列单元列车在运行过程中，距离相近，假设所受到坡道阻力相同，则b1和b2均为0。当列车处于平衡状态xe时，所有编组内的列车速度均保持一致，为了后续控制系统设计的方便，本文在平衡点处将式(6)线性化为
{˙xi,1(t)=ui−1(t)−ui(t)−aevi−1,i(t)˙xi,2(t)=ui(t)−ui+1(t)−aevi,i+1(t)˙xi,3(t)=evi,i−1(t)˙xi,4(t)=evi+1,i(t)a=[c1+2c2vr(t)]/m (7) 整理可得虚拟编组列车的状态空间模型为
˙xi(t)=Ai(t)xi(t)+Biui(t)+Ci(t) (8) Ai(t)=[−a0000−a0010000100]Bi=[−1100]Ci(t)=[ui−1(t)−ui+1(t)00] 式中：Ai(t)和Ci(t)均为t时刻列车i的连续状态空间模型矩阵系数；Bi为不随时间t变化的矩阵。
列车在实际运行过程中的状态信息通常是通过离散采样的方式传输的，因此，本文通过欧拉法将连续空间状态方程式(8)转化为离散形式(采样周期Ts=1 s)，即
{xi(tk+1)=Ai, s(tk)xi(tk)+Bi, sui(tk)+Ci, s(tk)Ai, s(tk)=Ai(tk)Ts+IBi, s=BiTsCi, s(tk)=Ci(tk)Ts (9) 式中：Ai, s(tk)、Bi, s和Ci, s(tk)均为第k个采样时刻tk时列车i的离散状态空间模型矩阵系数; I为单位矩阵。
2. 问题描述
2.1 虚拟编组列车运行安全约束
为了保证列车实际运行安全，引入状态约束和控制约束[5]。由于列车性能和其他因素的影响，列车控制力限制条件为
Umin (10) 式中：$U_{\text {min }}(t)$和$U_{\text {max }}(t)$分别为$t$时刻列车的最大制动减速度和最大牵引加速度。
考虑到轨道工况和天气影响，列车运行速度限制为
0 \leqslant v_{i}(t) \leqslant v_{\mathrm{lim}}(t) (11) 式中：$v_{\lim }(t)$为$t$时刻列车的最大速度限制。
在虚拟编组列车运行过程中，为了排除列车追尾的可能性，列车之间必须保持一定的安全间距，根据列车相对制动曲线可以计算出相邻列车间的安全距离约束为
s_{i-1}(t)-s_{i}(t)-L \geqslant d_{\min }+\max \left\{\frac{v_{i-1}^{2}(t)-v_{i}^{2}(t)}{2 U_{\min }(t)}, 0\right\} (12) 式中：dmin为相邻列车之间的最小运行间距。
由式(11)可知$v_{i-1}(t)+v_{i}(t) \leqslant 2 v_{\text {lim }}(t)$，因此，可将式(12)线性化为
\left\{\begin{array}{l}s_{i-1}(t)-s_{i}(t)-L \geqslant d_{\text {min }} \\ s_{i-1}(t)-s_{i}(t)-L \geqslant d_{\text {min }}+\frac{v_{\text {lim }}(t)}{U_{\min }(t)}\left[v_{i-1}(t)-v_{i}(t)\right]\end{array}\right. (13) 为后续描述方便，将上述安全约束表示成如下约束集形式
\begin{aligned} x_i(t) \in X_v & :=\left\{x_i(t): \eta_j\left[x_i(t)\right] \geqslant 0, j=1, 2, 3, 4\right\} \\ i \in \mathbb{N}: & =\{0, 1, \cdots, I\} \end{aligned} (14) \begin{aligned} x_i(t) \in X_s: & =\left\{x_i(t): \eta_j\left[x_i(t)\right] \geqslant 0, j=5, 6, 7, 8\right\} \\ i \in \mathbb{N}: & =\{1, 2, \cdots, I\} \end{aligned} (15) \begin{aligned} u_i(t) & \in U:=\left\{u_i(t): U_{\min }(t) \leqslant u_i(t) \leqslant U_{\max }(t)\right\} \\ i & \in \mathbb{N}:=\{0, 1, \cdots, I\} \end{aligned} (16) \begin{aligned} & \eta_1\left[x_i(t)\right]=-\boldsymbol{G}_1 \boldsymbol{x}_i(t)+v_{i-1}(t) \\ & \eta_2\left[x_i(t)\right]=\boldsymbol{G}_1 \boldsymbol{x}_i(t)+v_{\lim }(t)-v_{i-1}(t) \\ & \eta_3\left[x_i(t)\right]=\boldsymbol{G}_2 \boldsymbol{x}_i(t)+v_{i+1}(t) \\ & \eta_4\left[x_i(t)\right]=-\boldsymbol{G}_2 \boldsymbol{x}_i(t)+v_{\lim }(t)-v_{i+1}(t) \\ & \eta_5\left[x_i(t)\right]=\boldsymbol{G}_3 \boldsymbol{x}_i(t)+D-d_{\min } \\ & \eta_6\left[x_i(t)\right]=\left[\boldsymbol{G}_3-v_{\lim }(t) \boldsymbol{G}_1/U_{\min }(t)\right] x_i(t)+D-d_{\min } \\ & \eta_7\left[x_i(t)\right]=\boldsymbol{G}_4 \boldsymbol{x}_i(t)+D-d_{\min } \\ & \eta_8\left[x_i(t)\right]=\left[\boldsymbol{G}_4-v_{\lim }(t) \boldsymbol{G}_2/U_{\min }(t)\right] \boldsymbol{x}_i(t)+D-d_{\min } \end{aligned} 式中：$X_{v} 、X_{s} 、U$分别列车实际运行过程中的速度(v)约束集、位移($s$)约束集和控制输入约束集；$\mathbb{N}$为自然数集；$\boldsymbol{G}_{1}=(1, 0, 0, 0), \boldsymbol{G}_{2}=(0, 1, 0, 0)$, $\boldsymbol{G}_{3}=(0, 0, 1, 0), \boldsymbol{G}_{4}=(0, 0, 0, 1)$, 为$\eta_{j}(\cdot)$中各矩阵参数。
2.2 最优控制目标
在虚拟编组列车运行过程中，各单元列车之间保证一定的安全间距是控制系统首先要考虑的问题，而在列车以一定的安全间距运行时，各列车速度也必然是趋于一致的，以此保证稳定的编队运行状态；其次，在满足安全间距的前提下，控制力也应尽可能小，从而满足乘客舒适性的要求。为此，通过设计满足上述要求的性能指标函数，求出最优控制输入，具体表达形式为
\left\{\begin{array}{l} u_{i}^{*}(t)=\arg \min\limits_{u_{i}(t)} J\left[\boldsymbol{x}_{i}(t), u_{i}(t)\right] \\ J\left[\boldsymbol{x}_{i}(t), u_{i}(t)\right]=\left\|\boldsymbol{q} \boldsymbol{x}_{i}(t)\right\|_{2}+\left[r u_{i}(t)\right]^{2} \end{array}\right. (17) 式中: $J(\cdot)$为性能指标函数; $\boldsymbol{q}=\left(q_{\mathrm{v} 1}, q_{\mathrm{v} 2}, q_{\mathrm{s} 1}, q_{\mathrm{s} 2}\right)$, 为状态的加权系数向量；$r$为控制力的加权系数，通过设计$\boldsymbol{q}_{\mathrm{v}}=\left(q_{\mathrm{v} 1}, q_{\mathrm{v} 2}\right) 、\boldsymbol{q}_{\mathrm{s}}=\left(q_{\mathrm{s} 1}, q_{\mathrm{s} 2}\right)$和$r$来反映速度、间距和控制量三者的重要程度；$u_{i}^{*}(t)$为列车$i$在$t$时刻的最优控制量。
3. 虚拟编组列车DMPC控制器设计
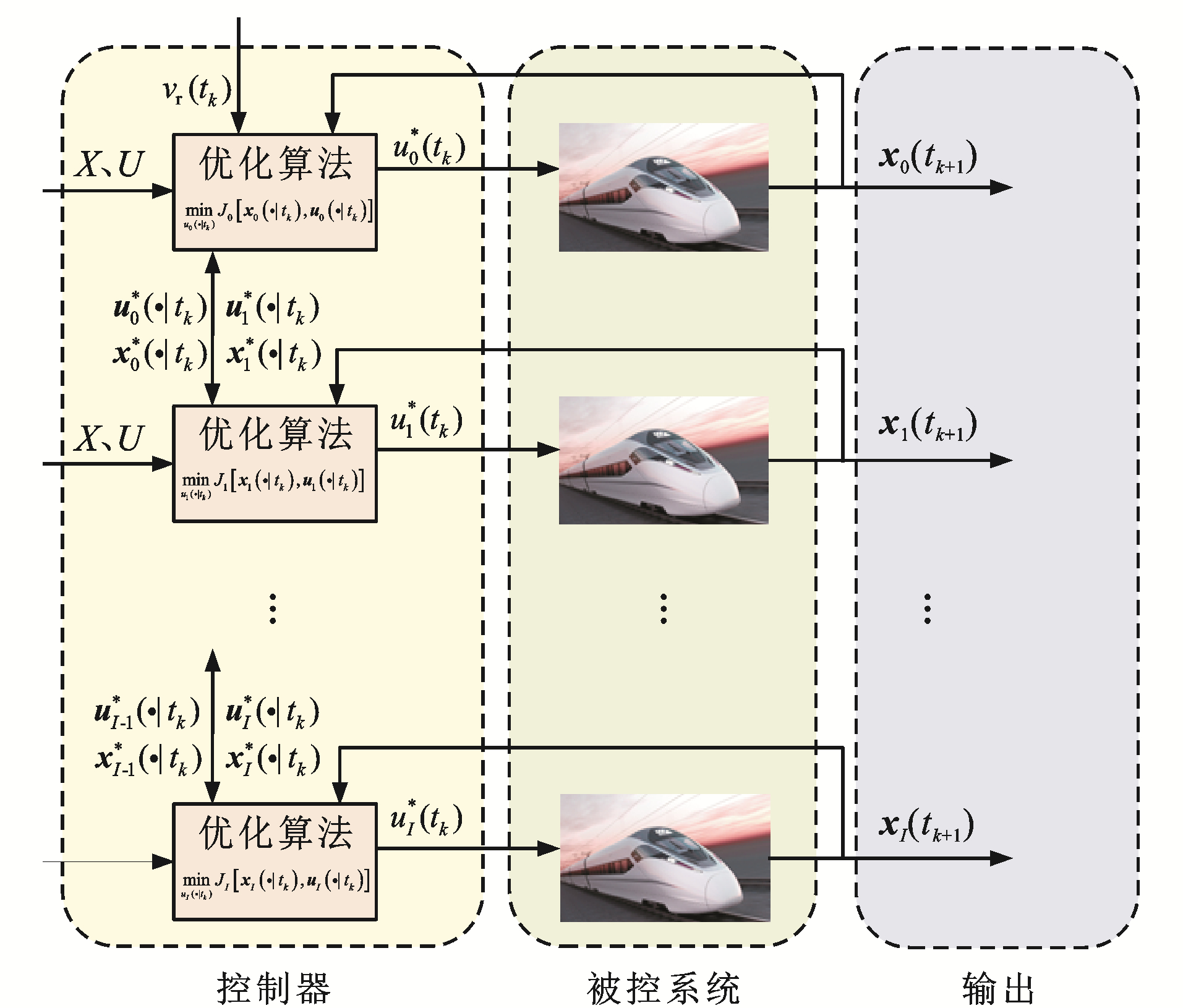
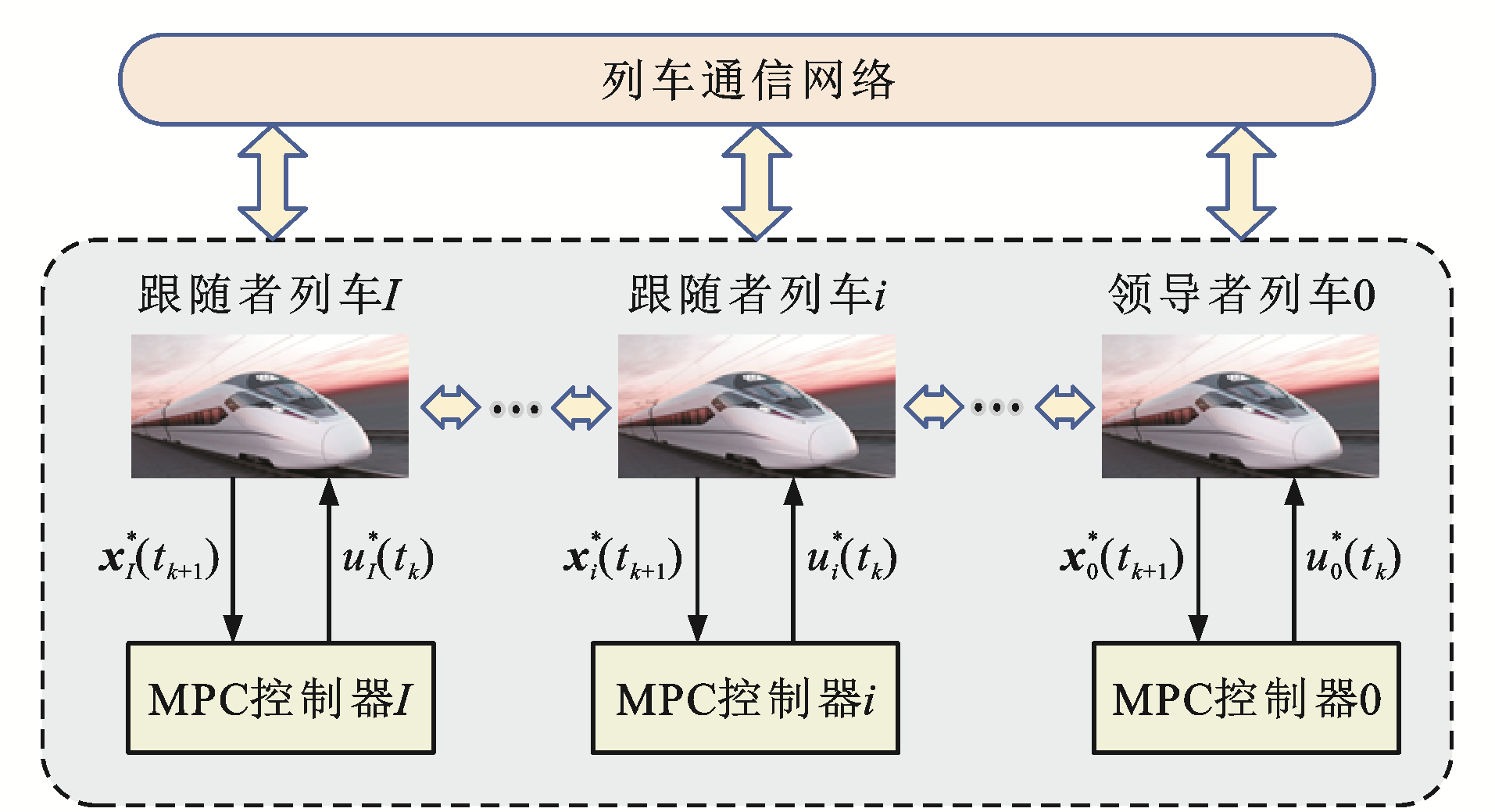
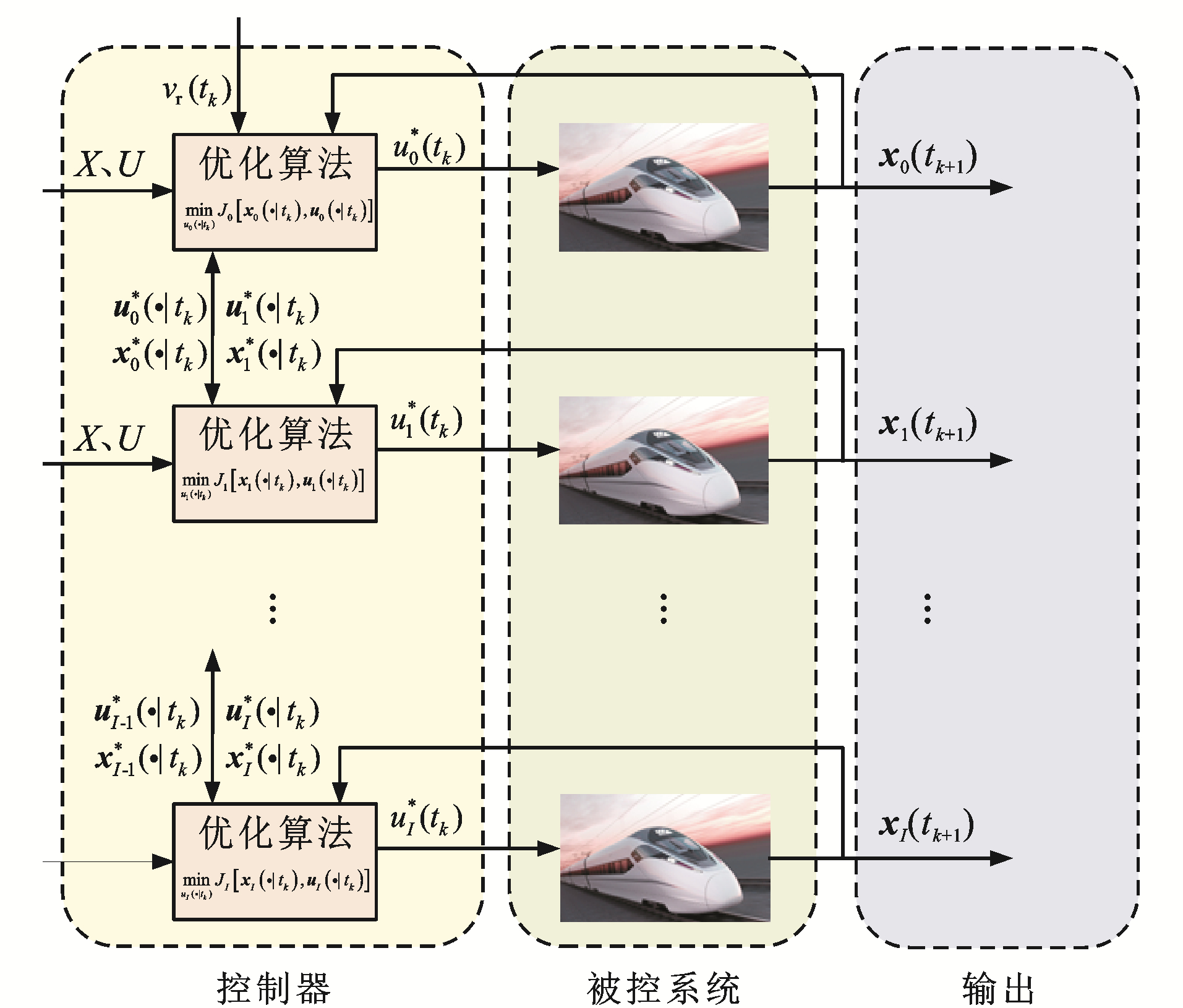
本文采用DMPC方法对虚拟编组列车进行跟踪控制。如图 2所示，DMPC策略下的虚拟编组列车含有多个控制器，即每列单元列车都配备一个MPC控制器，一对一地对本单元列车进行运行控制，$x_{i}^{*}\left(t_{k+1}\right)$为采样时刻$t_{k}$时列车$i$受最优控制量$u_{i}^{*}\left(t_{k}\right)$作用下在$t_{k+1}$时刻的最优状态量。这种DMPC控制方式可以很大程度地减轻控制器的运算负担，使运算更高效、更准确。
3.1 DMPC控制器设计
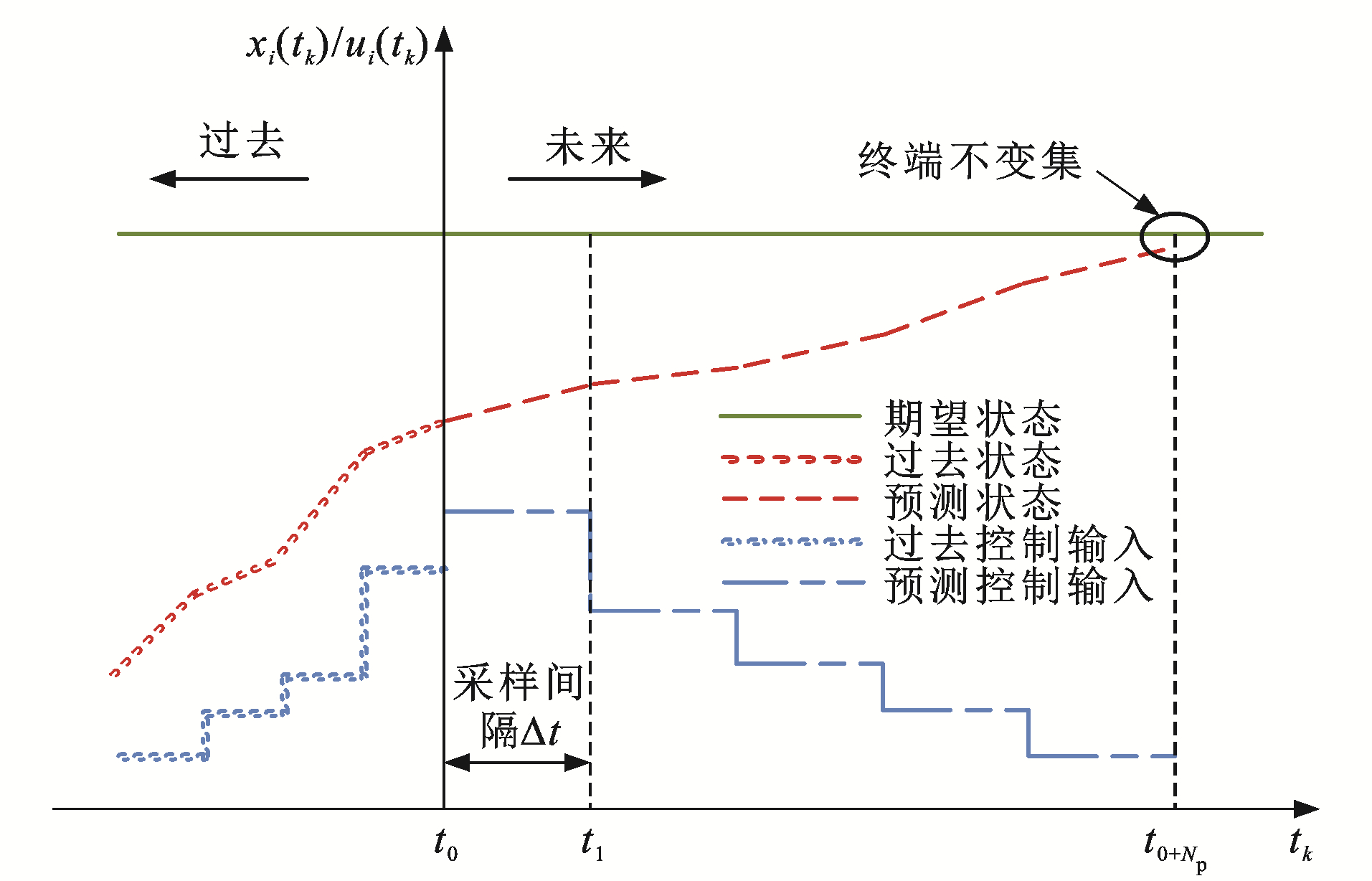
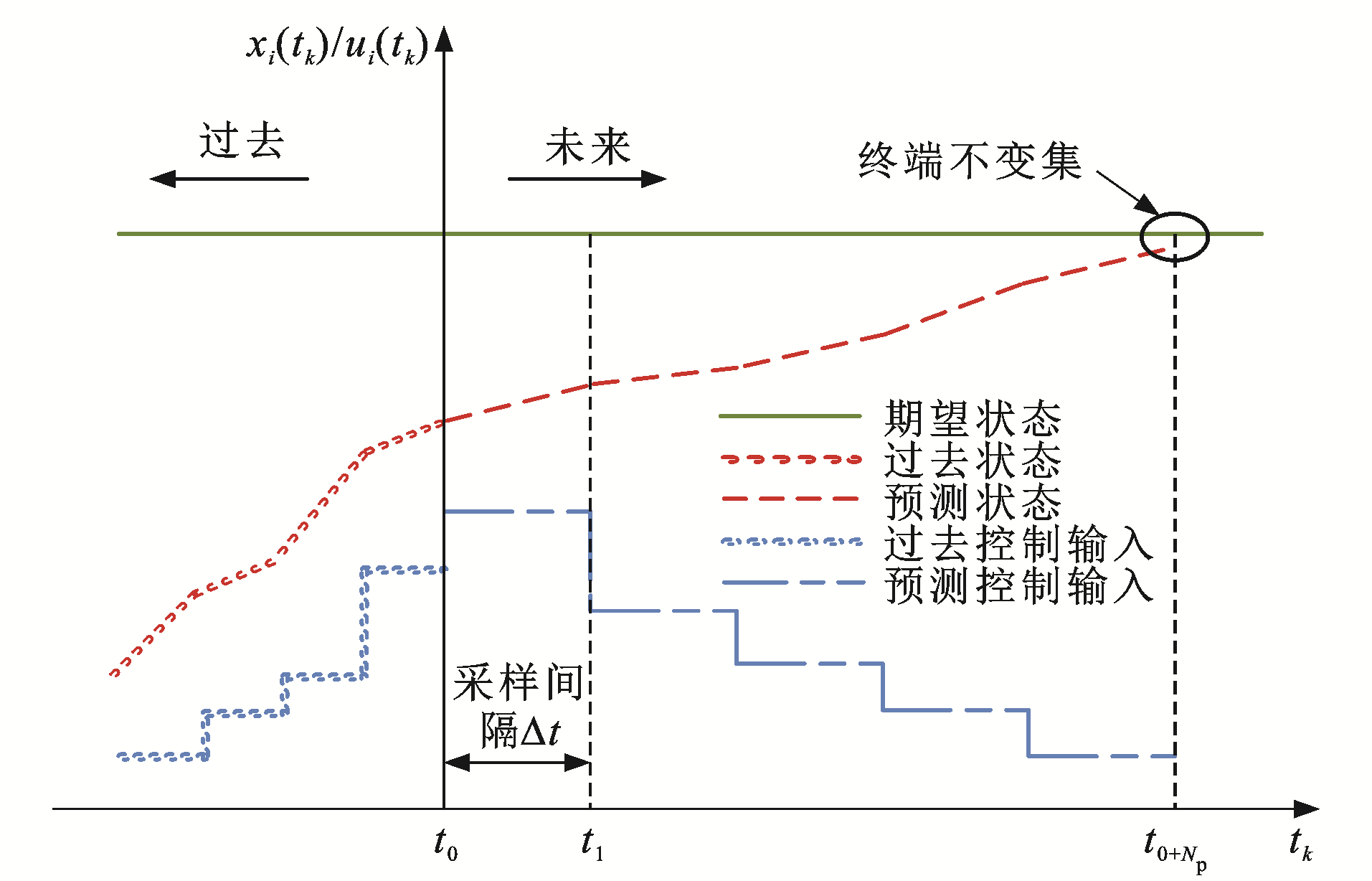
MPC是一种基于预测模型的闭环滚动优化控制算法，如图 3所示，在预测时域[tk, tk+Np](Np为预测时域最大步长)内，根据系统初始状态x(tk)、预测模型和约束条件，通过求解该时域内的性能指标函数求得最优控制序列及预测状态，将最优序列的第1项赋值给被控对象，完成一次迭代，并在下一个预测时域重复以上操作，直至全部轨迹预测完成。
根据式(8)得到的虚拟编组列车状态空间离散化模型，将其转换成MPC预测模型，即
\left\{\begin{array}{l} \boldsymbol{X}_i\left(t_k\right)=\boldsymbol{A}_{i, \mathrm{c}}\left(t_k\right) \boldsymbol{x}_i\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{c}}\left(t_k\right) \boldsymbol{U}_i\left(t_k\right)+\boldsymbol{C}_{i, \mathrm{c}}\left(t_k\right) \\ \boldsymbol{A}_{i, \mathrm{c}}\left(t_k\right)=\left(\boldsymbol{I}, \boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right), \boldsymbol{A}_{i, \mathrm{~s}}^2\left(t_k\right), \cdots, \boldsymbol{A}_{i, \mathrm{~s}}^{N_{\mathrm{p}}}\left(t_k\right)\right)^{\mathrm{T}} \\ \boldsymbol{C}_{i, \mathrm{c}}\left(t_k\right)=\left(\mathbf{0}, \boldsymbol{C}_{i, \mathrm{~s}}\left(t_k\right), 2 \boldsymbol{C}_{i, \mathrm{~s}}\left(t_k\right), \cdots, N_{\mathrm{p}} \boldsymbol{C}_{i, \mathrm{~s}}\left(t_k\right)\right)^{\mathrm{T}}\\ {B_{i, \mathrm{c}}\left(t_k\right)=\left[\begin{array}{ccccc} 0 & 0 & 0 & \cdots & 0 \\ B_{i, \mathrm{~s}} & 0 & 0 & \cdots & 0 \\ A_{i, \mathrm{~s}}\left(t_k\right) B_{i, \mathrm{~s}} & B_{i, \mathrm{~s}} & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & & \vdots \\ A_{i, \mathrm{~s}}^{N_{\mathrm{p}}-1}\left(t_k\right) B_{i, \mathrm{~s}} & A_{i, \mathrm{~s}}^{N_{\mathrm{p}}-2}\left(t_k\right) B_{i, \mathrm{~s}} & A_{i, \mathrm{~s}}^{N_{\mathrm{p}}-3}\left(t_k\right) B_{i, \mathrm{~s}} & \cdots & B_{i, \mathrm{~s}} \end{array}\right]}\\ \begin{aligned} & \boldsymbol{U}_i\left(t_k\right)=\left(u_i\left(t_k \mid t_k\right), u_i\left(t_{k+1} \mid t_k\right), \cdots, u_i\left(t_{k+N_{\mathrm{p}}-1} \mid t_k\right)\right) \\ & \boldsymbol{X}_i\left(t_k\right)=\left(\boldsymbol{x}_i\left(t_k \mid t_k\right), \boldsymbol{x}_i\left(t_{k+1} \mid t_k\right), \cdots, \boldsymbol{x}_i\left(t_{k+N_{\mathrm{n}}} \mid t_k\right)\right) \end{aligned} \end{array}\right. (18) 式中：$\boldsymbol{A}_{i, \mathrm{c}}\left(t_{k}\right) 、\boldsymbol{B}_{i, \mathrm{c}}\left(t_{k}\right)$和$\boldsymbol{C}_{i, \mathrm{c}}\left(t_{k}\right)$均为采样时刻$t_{k}$时列车$i$的预测模型矩阵系数；$\boldsymbol{U}_{i}\left(t_{k}\right)$为要求解的控制序列；$u_{i}\left(t_{k} \mid t_{k}\right)$为在$t_{k}$时刻预测的$t_{k}$时刻的控制量；$\boldsymbol{X}_{i}\left(t_{k}\right)$为对应的预测状态序列；$\boldsymbol{x}_{i}\left(t_{k} \mid t_{k}\right)$为在$t_{k}$时刻预测的$t_{k}$时刻的状态量。
为方便设计虚拟编组列车最优控制问题，现给出如下假设。
假设1：对于系统模型式(9)，给定自身状态、2个邻接状态的偏差权重系数矩阵$Q 、Q_{1} 、Q_{2}$和控制量的权重系数$R$，且$Q 、Q_{1}$和$Q_{2}$均正定对称，存在一个常数$\alpha>0$，一个正定对称矩阵$\boldsymbol{H}$以及一个局部状态反馈控制律$\boldsymbol{K} \boldsymbol{x}_{i}\left(t_{k}\right) \in U$，其中$\boldsymbol{K}$为局部状态反馈控制率矩阵系数，使得对任意终端状态量都有终端状态量集合$\varOmega=\left\{\boldsymbol{x}_{i}\left(t_{k}\right) \in X_{\mathrm{f}}: \boldsymbol{x}_{i}^{\mathrm{T}}\left(t_{k}\right) \boldsymbol{H} \boldsymbol{x}_{i}\left(t_{k}\right) \leqslant \alpha\right\}$, 其中终端状态矩阵$\boldsymbol{H}$满足
\left\{\begin{array}{l} \left(\boldsymbol{A}_{i, \mathrm{~s}}\left(t_{k}\right)+\boldsymbol{B}_{i, \mathbf{K}} \boldsymbol{K}\right)^{\mathrm{T}} \boldsymbol{H}\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_{k}\right)+\boldsymbol{B}_{i, \mathbf{s}} \boldsymbol{K}\right]-\boldsymbol{H}+\boldsymbol{Q}+R \boldsymbol{K}^{\mathrm{T}} \boldsymbol{K} \leqslant \mathbf{0} \\ \left(\boldsymbol{A}_{i, \mathbf{s}}\left(t_{k}\right)+\boldsymbol{B}_{i, \mathbf{S}} \boldsymbol{K}\right)^{\mathrm{T}} \boldsymbol{H}\left(\boldsymbol{A}_{i, \mathbf{s}}\left(t_{k}\right)+\boldsymbol{B}_{i, \mathbf{s}} \boldsymbol{K}\right)-\boldsymbol{H}+\boldsymbol{Q}_{1} \leqslant \mathbf{0} \\ \left(\boldsymbol{A}_{i, \mathbf{s}}\left(t_{k}\right)+\boldsymbol{B}_{i, \mathbf{S}} \boldsymbol{K}\right)^{\mathrm{T}} \boldsymbol{H}\left[\boldsymbol{A}_{i, \mathbf{s}}\left(t_{k}\right)+\boldsymbol{B}_{i, \mathbf{s}} \boldsymbol{K}\right]-\boldsymbol{H}+\boldsymbol{Q}_{2} \leqslant \mathbf{0} \end{array}\right. (19) 以保证虚拟编组列车与相邻列车一致性为控制目标，并考虑加入邻接系统的状态信息，根据假设1，将列车$i$的性能指标函数$J_{i}\left[\boldsymbol{x}_{i}\left(\cdot \mid t_{k}\right), \boldsymbol{u}_{i}\left(\cdot \mid t_{k}\right)\right]$设计为
\begin{aligned} & \min _{u_i \left(\cdot \mid t_k\right)} J_i\left[x_i\left(\cdot \mid t_k\right), u_i\left(\cdot \mid t_k\right)\right]=\min _{u_i\left(\cdot \mid t_k\right)} \sum\limits_{j=0}^{N_{\mathrm{p}}^{-1}}\left\{\left\|x_i\left(t_{k+j} \mid t_k\right)\right\|_{\boldsymbol{Q}}^2+\right. \\ & \left\|\boldsymbol{x}_i\left(t_{k+j} \mid t_k\right)-\boldsymbol{x}_{i-1}\left(t_{k+j} \mid t_k\right)\right\|{ }_{\boldsymbol{Q}_1}^2+ \\ & \left.\left\|\boldsymbol{x}_i\left(t_{k+j} \mid t_k\right)-\boldsymbol{x}_{i+1}\left(t_{k+j} \mid t_k\right)\right\| \boldsymbol{Q}_2^2+\left[R u_i\left(t_{k+j} \mid t_k\right)\right]^2\right\}+ \\ & \left\|\boldsymbol{x}_i\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)-\boldsymbol{x}_{i-1}\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right\|_{\boldsymbol{H}}^2+ \\ & \left\|\boldsymbol{x}_i\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)-\boldsymbol{x}_{i+1}\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right\|_{\boldsymbol{H}}^2+ \\ & \left\|\boldsymbol{x}_i\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right\|_{\boldsymbol{H}}^2 \end{aligned} (20) \text { s. t. } \boldsymbol{x}_i\left(t_{k+1}\right)=\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right) \boldsymbol{x}_i\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} u_i\left(t_k\right)+\boldsymbol{C}_{\boldsymbol{i}, \mathrm{s}}\left(t_k\right) (21) \boldsymbol{x}_i\left(\cdot \mid t_k\right) \in X (22) \boldsymbol{u}_i\left(\cdot \mid t_k\right) \in U (23) \boldsymbol{x}_i\left(t_{k+N_{\mathrm{p}}} \mid t_k\right) \in X_{\mathrm{f}} \subseteq X (24) 式中: $\boldsymbol{x}_{i}\left(\cdot \mid t_{k}\right)$和$\boldsymbol{u}_{i}\left(\cdot \mid t_{k}\right)$分别为列车$i$在$t_{k}$时刻预测出的$\left[t_{k}, t_{k+N_{\mathrm{p}}}\right]$时域内的状态和控制量，且$\boldsymbol{x}_{i}\left(t_{k} \mid t_{k}\right)=\boldsymbol{x}_{i}\left(t_{k}\right), \boldsymbol{x}_{i-1}\left(t_{k+j} \mid t_{k}\right)=\hat{\boldsymbol{x}}_{i-1}\left(t_{k+j} \mid t_{k-1}\right)$, $\boldsymbol{x}_{i+1}\left(t_{k+j} \mid t_{k}\right)=\hat{\boldsymbol{x}}_{i+1}\left(t_{k+j} \mid t_{k-1}\right), \hat{\boldsymbol{x}}_{i}\left(t_{k+j} \mid t_{k-1}\right)$为列车$i$在$t_{k-1}$时刻估计的$t_{k+j}$时刻的状态；$X$为状态约束集，包括$X_{\mathrm{s}}$和$X_{\mathrm{v}} ; X_{\mathrm{f}}$为终端状态约束集，即终端不变集，为保证算法稳定性，终端预测状态必须在终端不变集内；$\|\cdot\|_{\boldsymbol{Q}_{2}}^{2} 、\|\cdot\|_{\boldsymbol{Q}_{1}}^{2} 、\|\cdot\|_{\boldsymbol{Q}_{2}}^{2}$和$\|\cdot\|_{H}^{2}$分别为自身状态偏差、2个邻接状态偏差以及终端状态偏差权重矩阵的欧几里得范数。
列车$i$的估计状态$\hat{\boldsymbol{x}}_{i}\left(t_{k+j} \mid t_{k-1}\right)$构造为
\hat{\boldsymbol{x}}_{i}\left(t_{k+j} \mid t_{k-1}\right)= \begin{cases}\boldsymbol{x}_{i}^{*}\left(t_{k+j} \mid t_{k-1}\right) & j=0, 1, \cdots, N_{\mathrm{p}}-1 \\ {\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_{k}\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K} x_{i}^{*}\left(t_{k+N_{\mathrm{p}}-1} \mid t_{k-1}\right)\right.} & j=N_{\mathrm{p}}\end{cases} (25) 式中：$\boldsymbol{x}_{i}^{*}\left(t_{k+j} \mid t_{k-1}\right)$为列车$i$在$t_{k-1}$时刻预测的$t_{k+j}$时刻的最优状态量。
为方便求解，将式(20)描述为二次规划函数格式。首先，将式(20)整理为
\begin{aligned} & J_i\left[\boldsymbol{x}_i\left(\cdot \mid t_k\right), \boldsymbol{u}_i\left(\cdot \mid t_k\right)\right]=\boldsymbol{X}_i^{\mathrm{T}}\left(t_k\right) \overline{\boldsymbol{Q}} \boldsymbol{X}_i\left(t_k\right)+ \\ & \quad\left[\boldsymbol{X}_i\left(t_k\right)-\boldsymbol{X}_{i-1}\left(t_k\right)\right]^{\mathrm{T}} \overline{\boldsymbol{Q}}_1\left[\boldsymbol{X}_i\left(t_k\right)-\boldsymbol{X}_{i-1}\left(t_k\right)\right]+ \\ & \quad\left[\boldsymbol{X}_i\left(t_k\right)-\boldsymbol{X}_{i+1}\left(t_k\right)\right]^{\mathrm{T}} \overline{\boldsymbol{Q}}_2\left[\boldsymbol{X}_i\left(t_k\right)-\boldsymbol{X}_{i+1}\left(t_k\right)\right]+ \\ & \boldsymbol{U}_i^{\mathrm{T}}\left(t_k\right) \overline{\boldsymbol{R}} \boldsymbol{U}_i\left(t_k\right) \end{aligned} (26) \left\{\begin{array}{l} \overline{\boldsymbol{Q}}=\operatorname{diag}\left[\operatorname{diag}(\boldsymbol{Q})_{\left(N_{\mathrm{p}}-1\right) \times\left(N_{\mathrm{p}}-1\right)}, \boldsymbol{H}\right] \\ \overline{\boldsymbol{Q}}_1=\operatorname{diag}\left[\operatorname{diag}\left(\boldsymbol{Q}_1\right)_{\left(N_{\mathrm{p}}-1\right) \times\left(N_{\mathrm{p}}-1\right)}, \boldsymbol{H}\right] \\ \overline{\boldsymbol{Q}}_2=\operatorname{diag}\left[\operatorname{diag}\left(\boldsymbol{Q}_2\right)_{\left(N_{\mathrm{p}}-1\right) \times\left(N_{\mathrm{p}}-1\right)}, \boldsymbol{H}\right] \\ \overline{\boldsymbol{R}}=\operatorname{diag}(R)_{N_{\mathrm{p}} \times N_{\mathrm{p}}} \end{array}\right. 将式(18)代入式(26)，并进一步剔除无关的常数项，则可将其简化为
\left\{\begin{array}{l} J_{i}\left[\boldsymbol{x}_{i}\left(\cdot \mid t_{k}\right), \boldsymbol{u}_{i}\left(\cdot \mid t_{k}\right)\right] \Rightarrow \hat{J}_{i}\left[\boldsymbol{x}_{i}\left(\cdot \mid t_{k}\right), \boldsymbol{u}_{i}\left(\cdot \mid t_{k}\right)\right]= \\ \quad \boldsymbol{U}_{i}^{\mathrm{T}}\left(t_{k}\right)\left[\boldsymbol{B}_{i, \mathrm{c}}^{\mathrm{T}}\left(t_{k}\right)\left(\overline{\boldsymbol{Q}}+\overline{\boldsymbol{Q}}_{1}+\overline{\boldsymbol{Q}}_{2}\right) \boldsymbol{B}_{i, \mathrm{c}}\left(t_{k}\right)+\overline{\boldsymbol{R}}\right] \boldsymbol{U}_{i}\left(t_{k}\right)+ \\ \quad 2\left\{\left[\boldsymbol{x}_{i}^{\mathrm{T}}\left(t_{k}\right) \boldsymbol{A}_{i, \mathrm{c}}^{\mathrm{T}}\left(t_{k}\right)+\boldsymbol{C}_{i, \mathrm{c}}^{\mathrm{T}}\left(t_{k}\right)\right]\left(\overline{\boldsymbol{Q}}+\overline{\boldsymbol{Q}}_{1}+\overline{\boldsymbol{Q}}_{2}\right)-\right. \\ \quad\left.\boldsymbol{X}_{i-1}^{\mathrm{T}}\left(t_{k}\right) \overline{\boldsymbol{Q}}_{1}-\boldsymbol{X}_{i+1}^{\mathrm{T}}\left(t_{k}\right) \overline{\boldsymbol{Q}}_{2}\right\} \boldsymbol{B}_{i, \mathrm{c}}\left(t_{k}\right) \boldsymbol{U}_{i}\left(t_{k}\right)= \\ \quad\boldsymbol{U}_{i}^{\mathrm{T}}\left(t_{k}\right) M \boldsymbol{U}_{i}\left(t_{k}\right)+2 N \boldsymbol{U}_{i}\left(t_{k}\right) \\ M \triangleq \boldsymbol{B}_{i, \mathrm{c}}^{\mathrm{T}}\left(t_{k}\right)\left(\overline{\boldsymbol{Q}}+\overline{\boldsymbol{Q}}_{1}+\overline{\boldsymbol{Q}}_{2}\right) \boldsymbol{B}_{i, \mathrm{c}}\left(t_{k}\right)+\overline{\boldsymbol{R}} \\ N \triangleq\left\{\left[\boldsymbol{x}_{i}^{\mathrm{T}}\left(t_{k}\right) \boldsymbol{A}_{i, \mathrm{c}}^{\mathrm{T}}\left(t_{k}\right)+\boldsymbol{C}_{i, \mathrm{c}}^{\mathrm{T}}\left(t_{k}\right)\right]\left(\overline{\boldsymbol{Q}}+\overline{\boldsymbol{Q}}_{1}+\overline{\boldsymbol{Q}}_{2}\right)-\right. \\ \left.\quad \boldsymbol{X}_{i-1}^{\mathrm{T}}\left(t_{k}\right) \overline{\boldsymbol{Q}}_{1}-\boldsymbol{X}_{i+1}^{\mathrm{T}}\left(t_{k}\right) \overline{\boldsymbol{Q}}_{2}\right\} \boldsymbol{B}_{i, \mathrm{c}}\left(t_{k}\right) \end{array}\right. (27) 式中：$\hat{J}_{i}\left[\boldsymbol{x}_{i}\left(\cdot \mid t_{k}\right), \boldsymbol{u _ { i }}\left(\cdot \mid t_{k}\right)\right]$为近似性能指标函数；$M$和$N$均为系数。
根据约束条件式(21)~(24)，计算得到最优控制序列$\boldsymbol{u}_{i}^{*}\left(\cdot \mid t_{k}\right)$，选取第1个控制量$u_{i}^{*}\left(t_{k}\right)$输入到被控对象上，得到列车下一时刻状态$\boldsymbol{x}_{i}^{*}\left(t_{k+1}\right)$，并将其反馈给控制器，用于下一时刻的最优控制运算，同时将信息通过车车通信方式传递给前车与后车，具体算法如下。
初始化：令i=0，tk=0，初始化控制器各参数以及各单元列车的运行状态，并设置领导者列车的参考速度曲线，步骤如下。
(1) 将参考速度曲线输入领导者列车控制器中，并求解约束优化问题式(20)。
(2) 将求得的$\boldsymbol{u}_{0}^{*}\left(\cdot \mid t_{k}\right)$和$\boldsymbol{x}_{0}^{*}\left(\cdot \mid t_{k}\right)$保存传递至后行列车。
(3) 取最优控制序列$\boldsymbol{u}_{0}^{*}\left(\cdot \mid t_{k}\right)$的第1个控制量$u_{0}^{*}\left(t_{k}\right)$作为领导者列车的实际控制输入，求得下一时刻的运行状态输出。
(4) 求解跟随者列车约束优化问题式(20)。
(5) 将求得的$\boldsymbol{u}_{i}^{*}\left(\cdot \mid t_{k}\right)$和$\boldsymbol{x}_{i}^{*}\left(\cdot \mid t_{k}\right)$保存传递至前行列车与后行列车。
(6) 取最优控制序列$\boldsymbol{u}_{i}^{*}\left(\cdot \mid t_{k}\right)$的第1个控制量$u_{i}^{*}\left(t_{k}\right)$作为列车$i$的实际控制输入，求得下一时刻的运行状态输出。
(7) 如果$i<I$，返回步骤(4)，求解后行列车的约束优化问题；如果$i=I$，令$t_{k}=t_{k+1}$，返回步骤(1)。
为更直观地描述上述算法步骤，设计算法运行结构框图如图 4所示。
3.2 稳定性分析
定理1：若$t_{k}=0$时刻，约束优化问题$J_{i}\left[\boldsymbol{x}_{i}\left(\cdot \mid t_{k}\right)\right.$，$\left.\boldsymbol{u}_{i}\left(\cdot \mid t_{k}\right)\right]$存在可行解，则对于任何时刻$t_{k}>0$，该约束优化问题均存在可行解，且闭环系统是稳定的，同时系统状态趋于平衡点附近的终端约束领域Ω内。
证明：假设在$t_{k}$时刻约束优化问题$J_{i}\left[\boldsymbol{x}_{i}\left(\cdot \mid t_{k}\right)\right.$，$\left.\boldsymbol{u}_{i}\left(\cdot \mid t_{k}\right)\right]$解得的最优控制序列$\boldsymbol{u}_{i}^{*}\left(\cdot \mid t_{k}\right)$为
\boldsymbol{u}_{i}^{*}\left(\cdot \mid t_{k}\right)=\left\{u_{i}^{*}\left(t_{k+j} \mid t_{k}\right): j=0, 1, \cdots, N_{\mathrm{p}}-1\right\} (28) 对应的最优状态序列$\boldsymbol{x}_{i}^{*}\left(\cdot \mid t_{k}\right)$为
\boldsymbol{x}_{i}^{*}\left(\cdot \mid t_{k}\right)=\left\{\boldsymbol{x}_{i}^{*}\left(t_{k+j} \mid t_{k}\right): j=0, 1, \cdots, N_{\mathrm{p}}\right\} (29) 同理，在$t_{k+1}$时刻，约束优化问题$J_{i}\left[\boldsymbol{x}_{i}\left(\cdot \mid t_{k+1}\right)\right.$，$\left.\boldsymbol{u}_{i}\left(\cdot \mid t_{k+1}\right)\right]$解得的最优控制序列为
\begin{aligned} \boldsymbol{u}_i(\cdot & \left.\mid t_{k+1}\right)=\left\{u_i\left(t_{k+1+j} \mid t_{k+1}\right): j=0, 1, \cdots, N_{\mathrm{p}}-1\right\}= \\ & \left\{u_i\left(t_{k+1} \mid t_{k+1}\right), u_i\left(t_{k+2} \mid t_{k+1}\right), \cdots, u_i\left(t_{k+N_{\mathrm{p}}-1} \mid t_{k+1}\right), \right. \\ & \left.u_i\left(t_{k+N_{\mathrm{p}}} \mid t_{k+1}\right)\right\}=\left\{u_i^*\left(t_{k+1} \mid t_k\right), u_i^*\left(t_{k+2} \mid t_k\right), \cdots, \right. \\ & \left.u_i^*\left(t_{k+N_{\mathrm{p}}-1} \mid t_k\right), \boldsymbol{K} \boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right\} \end{aligned} (30) 由假设1可知，$\boldsymbol{x}_{i}^{*}\left(t_{k+N_{\mathrm{p}}} \mid t_{k}\right) \in \varOmega$且$u_{i}^{*}\left(t_{k+N_{\mathrm{p}}} \mid t_{k}\right)=$ $\boldsymbol{K} \boldsymbol{x}_{i}^{*}\left(t_{k+N_{\mathrm{p}}} \mid t_{k}\right) \in U$，则可得
\begin{aligned} & \boldsymbol{x}_i\left(t_{k+N_{\mathrm{p}}+1} \mid t_{k+1}\right)=\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right) \boldsymbol{x}_i\left(t_{k+N_{\mathrm{p}}} \mid t_{k+1}\right)+ \\ & \quad \boldsymbol{B}_{i, \mathrm{~s}} u_i\left(t_{k+N_{\mathrm{p}}} \mid t_{k+1}\right)=\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right] \cdot \\ & \quad \boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right) \end{aligned} (31) $t_{k+1}$时刻对应的状态序列$\boldsymbol{x}_{i}\left(\cdot \mid t_{k+1}\right)$为
\begin{aligned} \boldsymbol{x}_i(\cdot & \left.\mid t_{k+1}\right)=\left\{\boldsymbol{x}_i\left(t_{k+1+j} \mid t_{k+1}\right): j=0, 1, \cdots, N_{\mathrm{p}}\right\}= \\ & \left\{\boldsymbol{x}_i\left(t_{k+1} \mid t_{k+1}\right), \boldsymbol{x}_i\left(t_{k+2} \mid t_{k+1}\right), \cdots, \boldsymbol{x}_i\left(t_{k+N_{\mathrm{p}}} \mid t_{k+1}\right)\right\}= \\ & \left\{\boldsymbol{x}_i^*\left(t_{k+1} \mid t_k\right), \boldsymbol{x}_i^*\left(t_{k+2} \mid t_k\right), \cdots, \boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}-1} \mid t_k\right), \right. \\ & {\left.\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right] \boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right\} } \end{aligned} (32) $\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_{k}\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right] \boldsymbol{x}_{i}^{*}\left(t_{k+N_{\mathrm{p}}} \mid t_{k}\right) \in \varOmega$，则可得
\boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}+1}\right)=\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right] \boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right) \in X_{\mathrm{f}} \subseteq X (33) 在$t_{k+1}$时刻，该约束优化问题存在可行解，而在$t_{k}=0$时刻，该约束优化问题存在可行解，所以在任何时刻$t_{k}>0$，该约束优化问题均存在可行解。
由式(20)可知，tk时刻对应的目标函数为
\begin{align*} & J_{i}\left[\boldsymbol{x}_{i}\left(\cdot \mid t_{k}\right), \boldsymbol{u}_{i}\left(\cdot \mid t_{k}\right)\right]=\sum\limits_{j=0}^{N_{\mathrm{p}}-1}\left\{\left\|\boldsymbol{x}_{i}\left(t_{k+j} \mid t_{k}\right)\right\|_{\boldsymbol{Q}}^{2}+\right. \\ & \\ & \quad\left\|\boldsymbol{x}_{i}\left(t_{k+j} \mid t_{k}\right)-\boldsymbol{x}_{i-1}\left(t_{k+j} \mid t_{k}\right)\right\|_{\boldsymbol{Q}_{1}}^{2}+ \\ & \\ & \quad\left\|\boldsymbol{x}_{i}\left(t_{k+j} \mid t_{k}\right)-\boldsymbol{x}_{i+1}\left(t_{k+j} \mid t_{k}\right)\right\|_{\boldsymbol{Q}_{2}}^{2}+ \\ & \\ & \left.\quad\left[R u_{i}\left(t_{k+j} \mid t_{k}\right)\right]^{2}\right\}+\| \boldsymbol{x}_{i}\left(t_{k+N_{\mathrm{p}}} \mid t_{k}\right)- \\ & \quad \boldsymbol{x}_{i-1}\left(t_{k+N_{\mathrm{p}}} \mid t_{k}\right) \|_{\boldsymbol{H}}^{2}+\left\|\boldsymbol{x}_{i}\left(t_{k+N_{\mathrm{p}}} \mid t_{k}\right)\right\|_{\boldsymbol{H}}^{2}+ \\ & \quad\left\|\boldsymbol{x}_{i}\left(t_{k+N_{\mathrm{p}}} \mid t_{k}\right)-\boldsymbol{x}_{i+1}\left(t_{k+N_{\mathrm{p}}} \mid t_{k}\right)\right\|_{\boldsymbol{H}}^{2} \end{align*} (34) 将式(30)和(32)代入式(20)，计算出tk+1时刻对应的目标函数为
\begin{gathered} J_i\left[x_i\left(\cdot \mid t_{k+1}\right), \boldsymbol{u}_i\left(\cdot \mid t_{k+1}\right)\right]=\sum\limits_{j=0}^{N_{\mathrm{p}}-1}\left\{\left\|\boldsymbol{x}_i\left(t_{k+j+1} \mid t_{k+1}\right)\right\|_{\boldsymbol{Q}}^2+\right. \\ \left\|\boldsymbol{x}_{\boldsymbol{k}}\left(t_{k+j+1} \mid t_{k+1}\right)-\boldsymbol{x}_{i-1}\left(t_{k+j+1} \mid t_{k+1}\right)\right\|_{\boldsymbol{Q}_1}^2+ \\ \left\|\boldsymbol{x}_i\left(t_{k+j+1} \mid t_{k+1}\right)-\boldsymbol{x}_{i+1}\left(t_{k+j+1} \mid t_{k+1}\right)\right\|_{\boldsymbol{Q}_2}+ \\ \left.\left.\left[R u_i\left(t_{k+j+1} \mid t_{k+1}\right)\right)^2\right]+\left\|\boldsymbol{x}_i\left(t_{k+j+1} \mid t_{k+1}\right)\right\|_{\boldsymbol{H}}^2\right\}+\\ \left\|\boldsymbol{x}_i\left(t_{k+N_{\mathrm{p}}+1} \mid t_{k+1}\right)-\boldsymbol{x}_{i-1}\left(t_{k+N_{\mathrm{p}}+1} \mid t_{k+1}\right)\right\|_{\boldsymbol{H}}^2+ \\ \left\|\boldsymbol{x}_i\left(t_{k+N_{\mathrm{p}}+1} \mid t_{k+1}\right)-\boldsymbol{x}_{i+1}\left(t_{k+N_{\mathrm{p}}+1} \mid t_{k+1}\right)\right\|_{\boldsymbol{H}}^2 \end{gathered} (35) 由式(33)可将式(35)改写为
\begin{aligned} & J_i\left[x_i\left(\cdot \mid t_{k+1}\right), \boldsymbol{u}_i\left(\cdot \mid t_{k+1}\right)\right]=\sum\limits_{j=0}^{N_{\mathrm{p}}-2}\left\{\left\|x_i^*\left(t_{k+j+1} \mid t_k\right)\right\|_\boldsymbol{Q}^2+\right. \\ & \left\|\boldsymbol{x}_i^*\left(t_{k+j+1} \mid t_k\right)-\boldsymbol{x}_{i-1}\left(t_{k+j+1} \mid t_k\right)\right\|_{\boldsymbol{Q}_1}^2+ \\ & \left\|\boldsymbol{x}_i^*\left(t_{k+j+1} \mid t_k\right)-\boldsymbol{x}_{i+1}\left(t_{k+j+1} \mid t_k\right)\right\|_{\boldsymbol{Q}_2}^2+ \\ & \left.\left[R u_i^*\left(t_{k+j+1} \mid t_k\right)\right]^2\right\}+ \\ & \left\|\boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right\|_\boldsymbol{Q}^2+\left[R \boldsymbol{K} \boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right]^2+ \\ & \left\|\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right] \boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right\|_{\boldsymbol{H}}^2+ \\ & \left\|\boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)-\boldsymbol{x}_{i-1}\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right\|_{\boldsymbol{Q}_1}^2+ \\ & \left\|\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]\left[\boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)-\boldsymbol{x}_{i-1}\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right]\right\|_{\boldsymbol{H}}^2+ \\ & \left\|\boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)-\boldsymbol{x}_{i+1}\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right\|_{\boldsymbol{Q}_2}^2+ \\ & \left\|\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]\left[\boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)-\boldsymbol{x}_{i+1}\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right]\right\|_{\boldsymbol{H}}^2 \end{aligned} (36) 由式(36)可得
\begin{aligned} & J_i\left[\boldsymbol{x}_i\left(\cdot \mid t_{k+1}\right), \boldsymbol{u}_i\left(\cdot \mid t_{k+1}\right)\right]=J\left[\boldsymbol{x}_i\left(\cdot \mid t_k\right), \boldsymbol{u}_i\left(\cdot \mid t_k\right)\right]-\left\|\boldsymbol{x}_i^*\left(t_k \mid t_k\right)\right\| 2_{\boldsymbol{Q}_1}^2-\left\|\boldsymbol{x}_i^*\left(t_k \mid t_k\right)-\boldsymbol{x}_{i-1}\left(t_k \mid t_k\right)\right\| \boldsymbol{Q}_2- \\ & \left(R u_i^*\left(t_k \mid t_k\right)\right)^2+\left\|\boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)\right\|{ }_\boldsymbol{Q}^2+\boldsymbol{K}^{\mathrm{T}} R \boldsymbol{K}+\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]^{\mathrm{T}} \boldsymbol{H}\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]+\| \boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)- \\ & \boldsymbol{x}_{i-1}\left(t_{k+N_{\mathrm{p}}} \mid t_k\right) \|_{\boldsymbol{Q}_1+\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]^{\mathrm{T}} \boldsymbol{H}\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]+\left\|\boldsymbol{x}_i^*\left(t_{k+N_{\mathrm{p}}} \mid t_k\right)-\boldsymbol{x}_{i+1}\left(t_{k+N} \mid t_k\right)\right\|_{\boldsymbol{Q}_2}^2+\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]^{\mathrm{T}} \boldsymbol{H}\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]} \end{aligned} (37) 由假设1可知
\left\{\begin{array}{l} {\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]^{\mathrm{T}} \boldsymbol{H}\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]-\boldsymbol{H}+\boldsymbol{Q}+R \boldsymbol{K}^{\mathrm{T}} \boldsymbol{K} \leqslant \mathbf{0}} \\ {\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]^{\mathrm{T}} \boldsymbol{H}\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]-\boldsymbol{H}+\boldsymbol{Q}_1 \leqslant \mathbf{0}} \\ {\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]^{\mathrm{T}} \boldsymbol{H}\left[\boldsymbol{A}_{i, \mathrm{~s}}\left(t_k\right)+\boldsymbol{B}_{i, \mathrm{~s}} \boldsymbol{K}\right]-\boldsymbol{H}+\boldsymbol{Q}_2 \leqslant \mathbf{0}} \end{array}\right. (38) J_i\left[\boldsymbol{x}_i\left(\cdot \mid t_{k+1}\right), \boldsymbol{u}_i\left(\cdot \mid t_{k+1}\right)\right] \leqslant J_i\left[\boldsymbol{x}_i\left(\cdot \mid t_k\right), \boldsymbol{u}_i\left(\cdot \mid t_k\right)\right] (39) 当$t_{k} \geqslant 0$时，$J_{i}\left[\boldsymbol{x}_{i}\left(\cdot \mid t_{k}\right), \boldsymbol{u}_{i}\left(\cdot \mid t_{k}\right)\right] \geqslant 0$，则该目标函数单调有界递减，系统闭环稳定且系统状态趋于平衡点附近的终端约束领域$\varOmega$内。
定理1得证。
4. 仿真分析
为了验证所提方法的有效性，采用实验室配备的高速列车追踪运行半实物仿真平台进行仿真，试验台装置如图 5所示。该试验平台通过一个编程扩展接口与用户端连接，如图 6所示，用户可以将列车系统参数、轨道信息以及所调试的控制算法程序输入到该测试平台中进行仿真，该平台可以支持Python、MATLAB等编程语言，本文采用MATLAB语言编写控制算法。仿真结果在试验台可视化系统和用户端均可以显示。本文以4列CRH380A单元列车组成的虚拟编组列车为控制对象，假设4列单元列车质量均为480 t，具体参数特性见表 1。
图 5 CRH380A高速列车虚拟编组模拟试验台Figure 5. Simulation test bench for CRH380A high-speed train virtual coupling表 1 系统参数Table 1. System parameters参数 取值 单元列车质量m/t 480 单元列车车长L/m 100 基本运行阻力系数c0/(N·kg-1) 0.755 0 基本运行阻力系数c1/(N·h·kg-1·km-1) 0.006 36 基本运行阻力系数c2/(N·h2·kg-1·km-2) 0.000 115 最大加速度Umax(t)/(m·s-2) 1 最小加速度Umin(t)/(m·s-2) 1 4.1 仿真设置
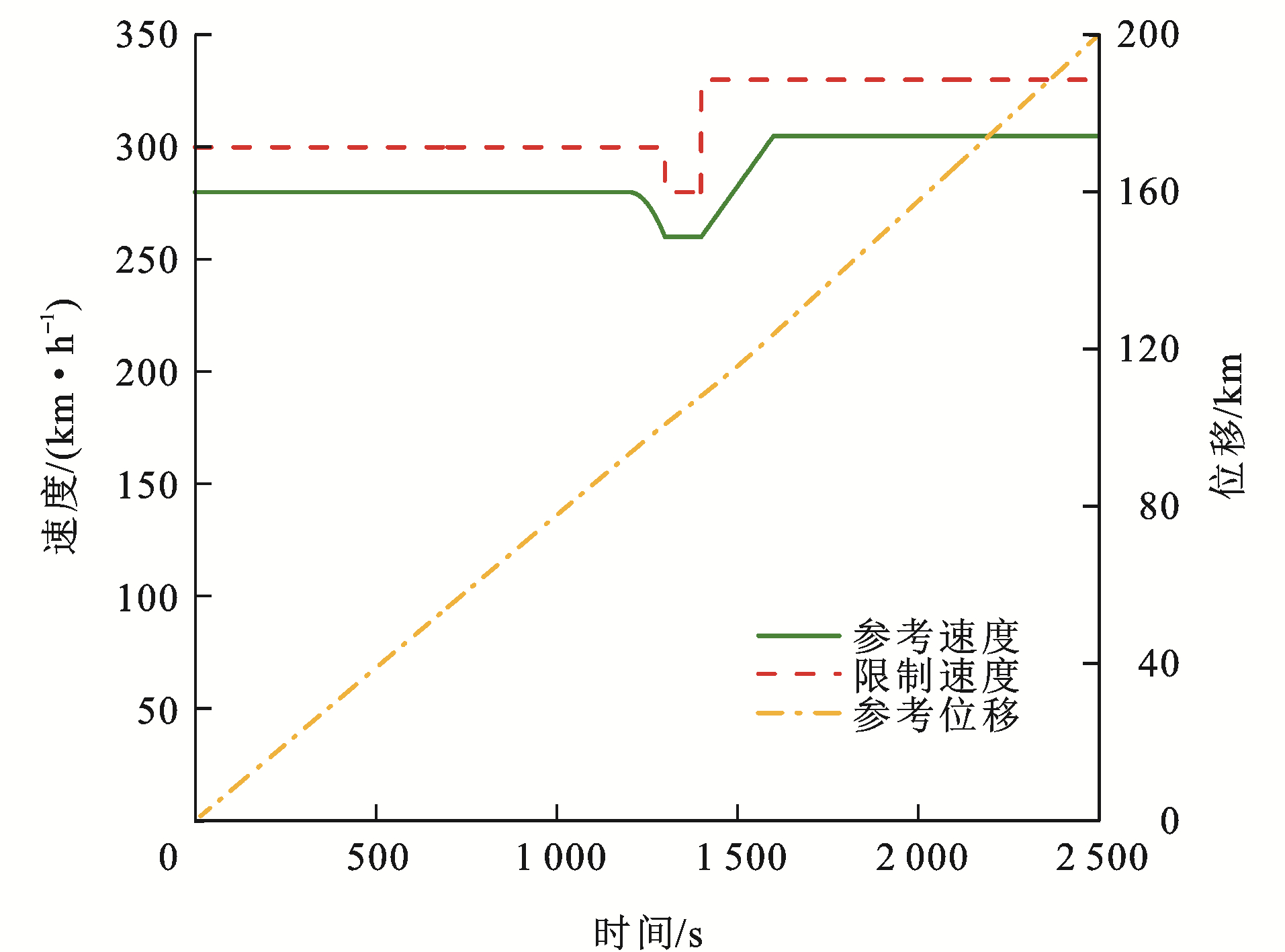
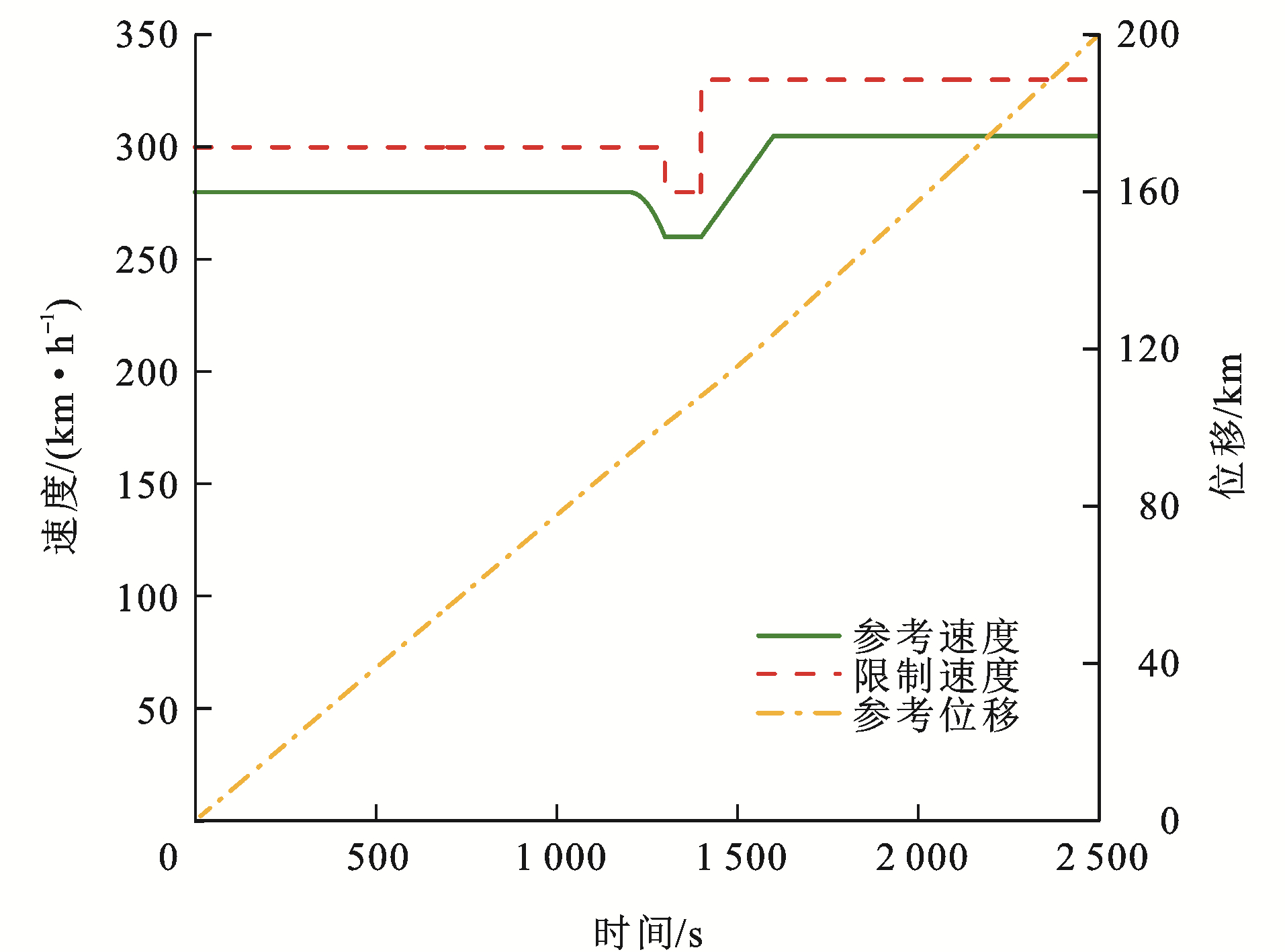
本文设置列车之间的期望距离$D$为100 m；最小运行间距$d_{\text {min }}$为50 m。图 7为领导者列车运行跟踪曲线，其中包括列车加速、惰行、制动3种工况，且在不同路段限制速度不同，系统采样时间间隔为1 s，采集样本数为2500个。
试验分为3组：第1组在不同初始状态下，采用DMPC方法对4列单元列车进行编队控制，以验证算法的稳定性；第2组采用本文控制方法、CMPC方法和已有DMPC方法分别对4列单元列车进行仿真，以验证本文算法的优势；第3组对3列跟随者列车的控制器结构输出时间进行仿真，以验证算法的实时性。
将CMPC方法下的虚拟编组列车状态空间方程设置为
\left\{\begin{array}{l} \dot{\boldsymbol{x}}(t)= \boldsymbol{A}^{\prime}(t) \boldsymbol{x}(t)+\boldsymbol{B}^{\prime} \boldsymbol{u}(t)+\boldsymbol{C}^{\prime}(t) \\ \boldsymbol{u}(t)= \left(u_0(t), u_1(t), u_2(t), u_3(t)\right)^{\mathrm{T}} \\ \boldsymbol{x}(t)= \left(e_{v_{\mathrm{r}, 0}}(t), e_{v_{0, 1}}(t), e_{v_{1, 2}}(t), e_{v_{2, 3}}(t), \right. \\ \;\;\;\;\;\;\;\;\; \left.e_{s_{0.1}}(t), e_{s_{1, 2}}(t), e_{s_{2, 3}}(t)\right)^{\mathrm{T}}\\ \boldsymbol{A}^{\prime}(t)=\left[\begin{array}{ccccccc} -a & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & -a & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & -a & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -a & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \end{array}\right]\\ \boldsymbol{B}^{\prime}=\left[\begin{array}{cccc} -1 & 0 & 0 & 0 \\ 1 & -1 & 0 & 0 \\ 0 & 1 & -1 & 0 \\ 0 & 0 & 1 & -1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{array}\right]\\ \boldsymbol{C}^{\prime}(t)=\left(u_{\mathrm{r}}(t), 0, 0, 0, 0, 0, 0\right)^{\mathrm{T}} \end{array}\right. (40) 式中：$\boldsymbol{u}(t)$为控制输入向量；$\boldsymbol{x}(t)$为输出状态向量；$u_{\mathrm{r}}(t)$为参考控制量。
4.2 不同初始条件下仿真分析
为了验证本文方法的有效性，考虑在不同初始条件下进行仿真，具体测试参数设置如表 2所示。
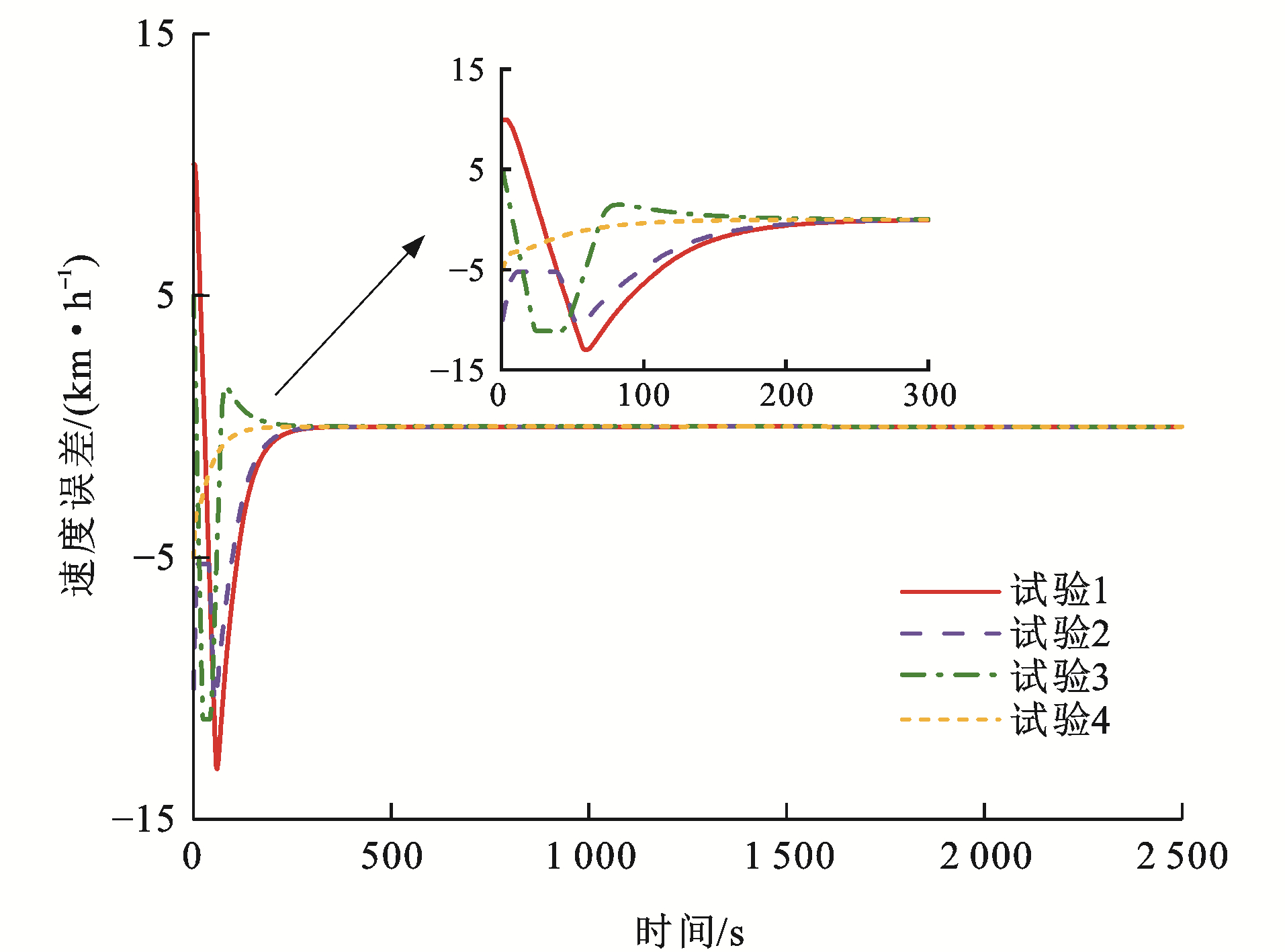
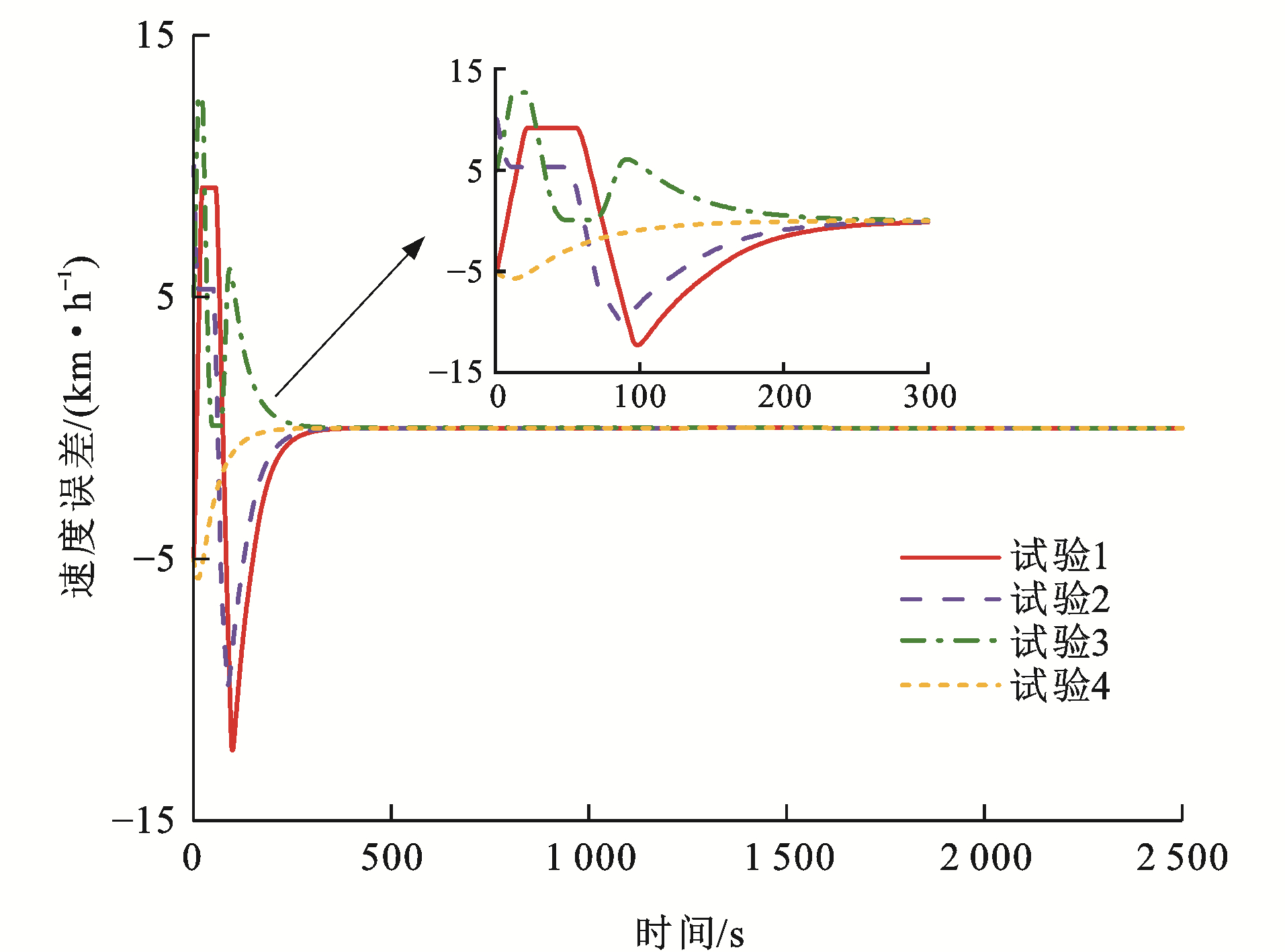
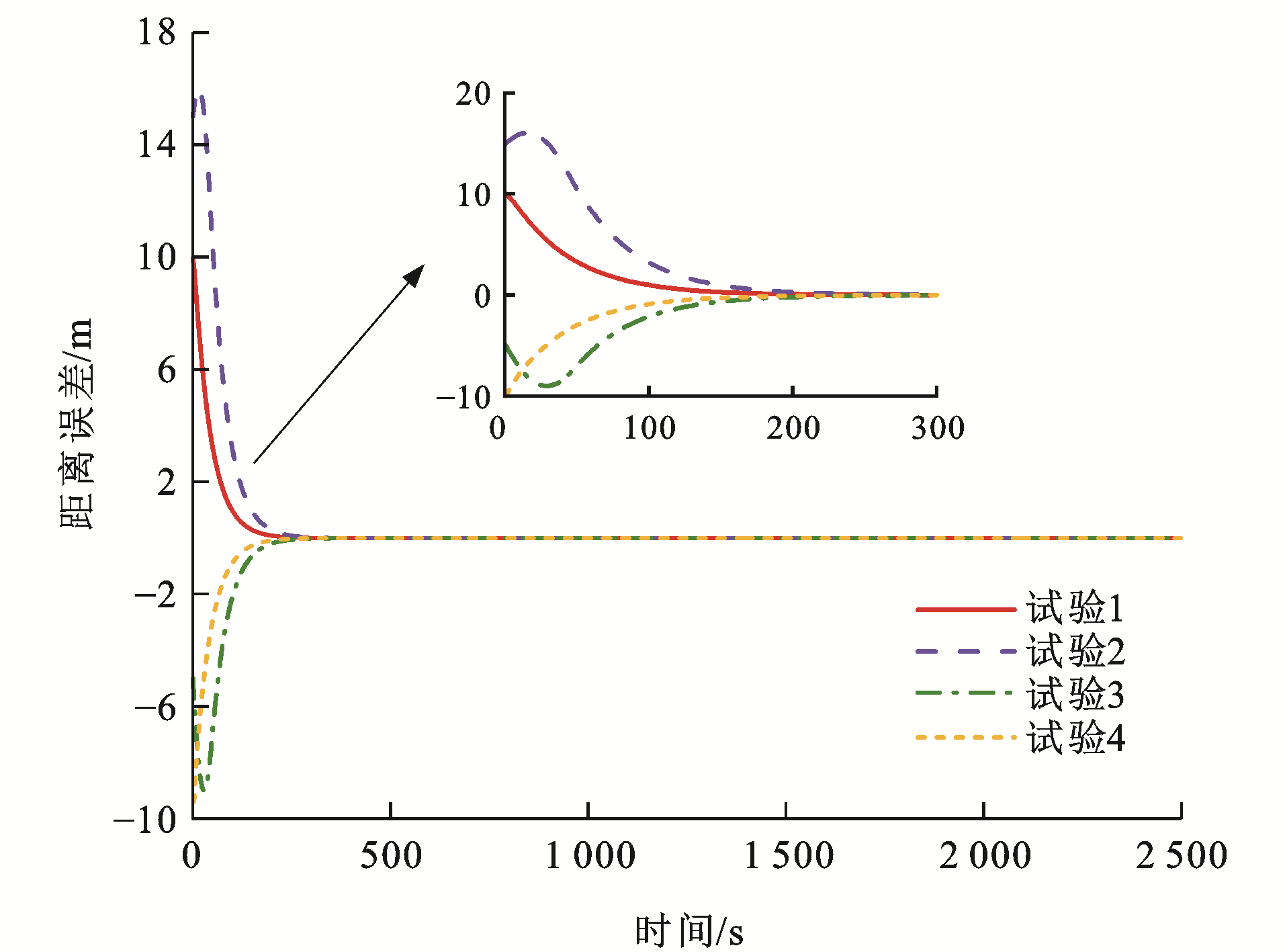
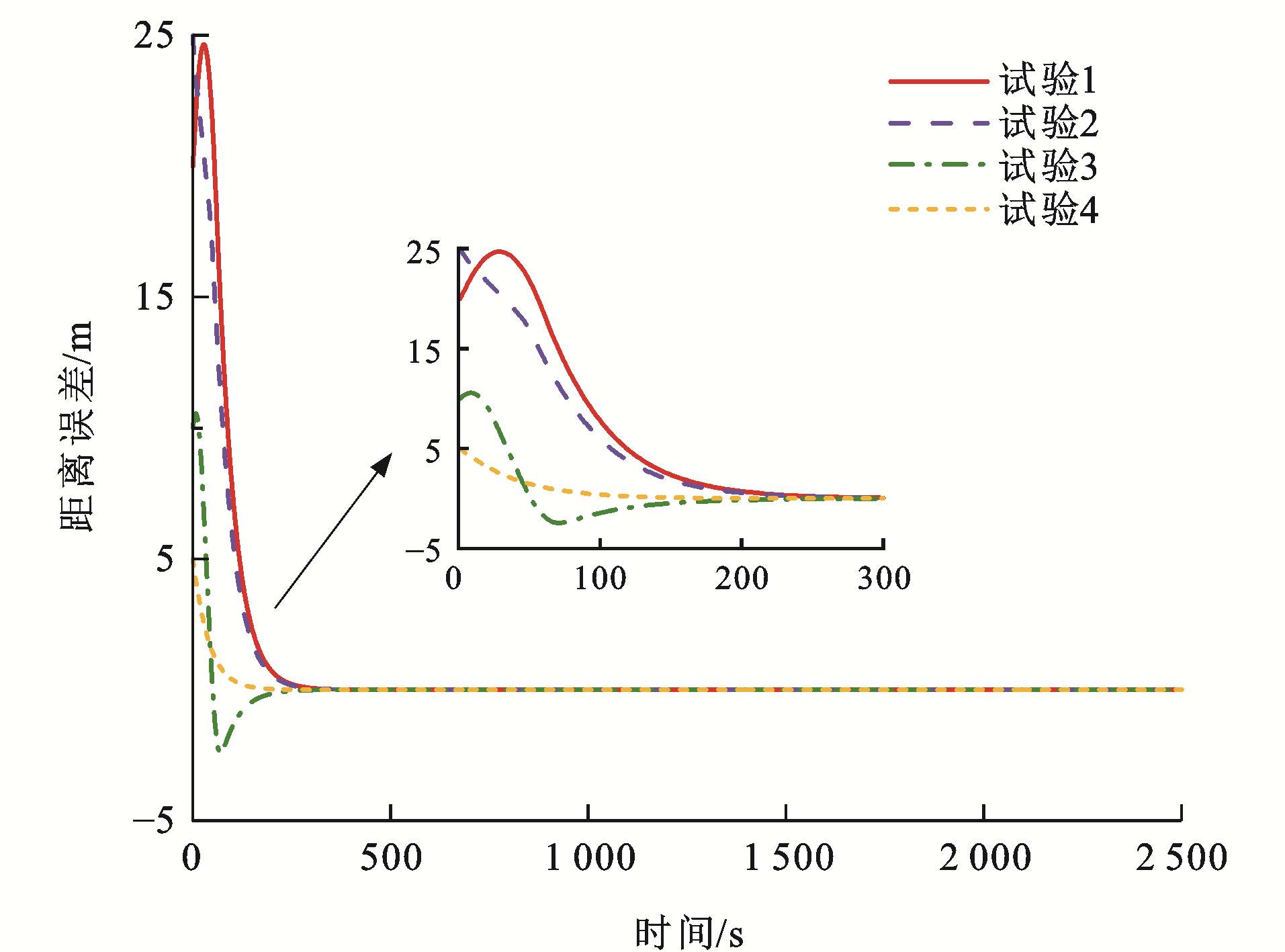
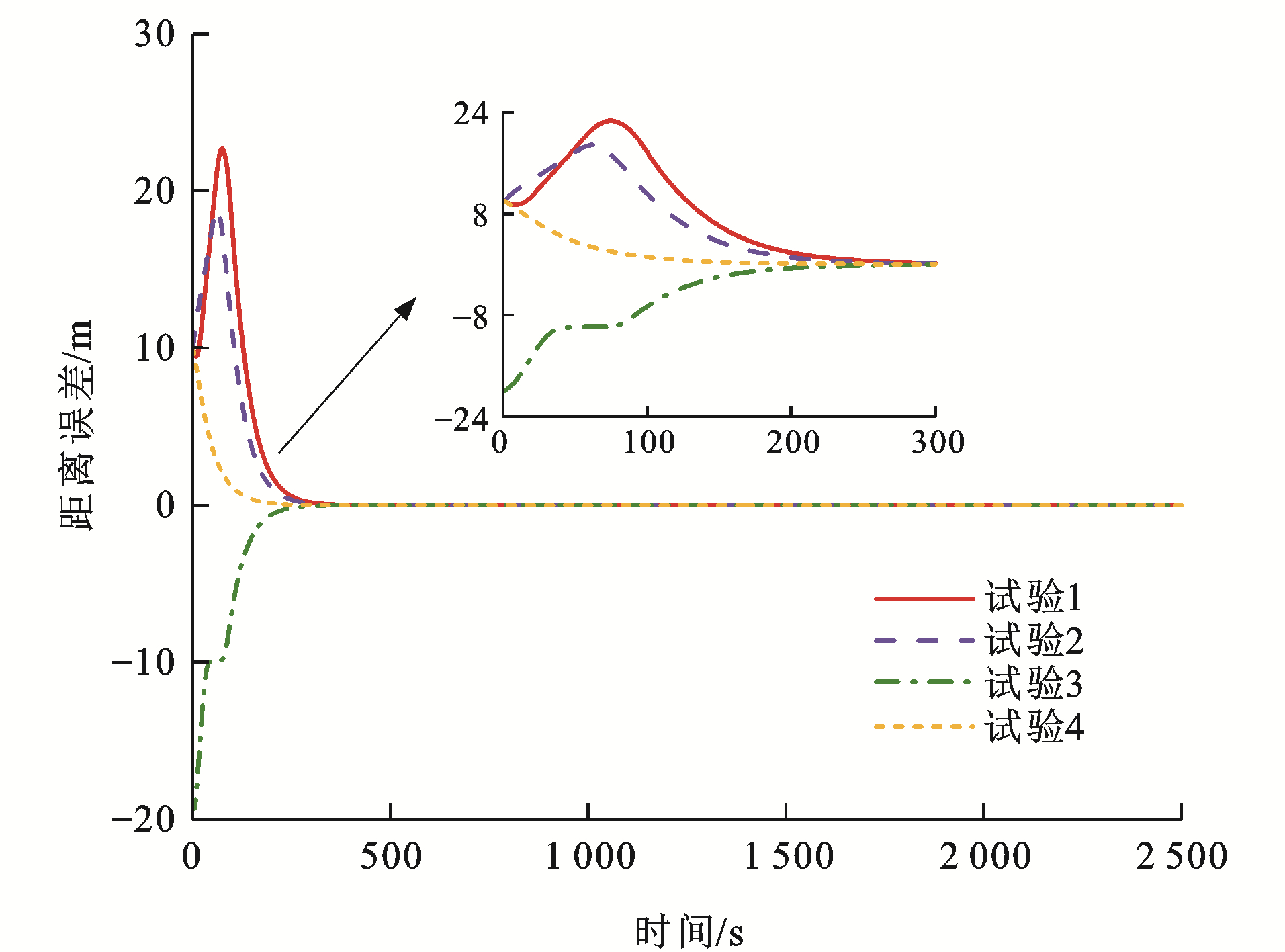
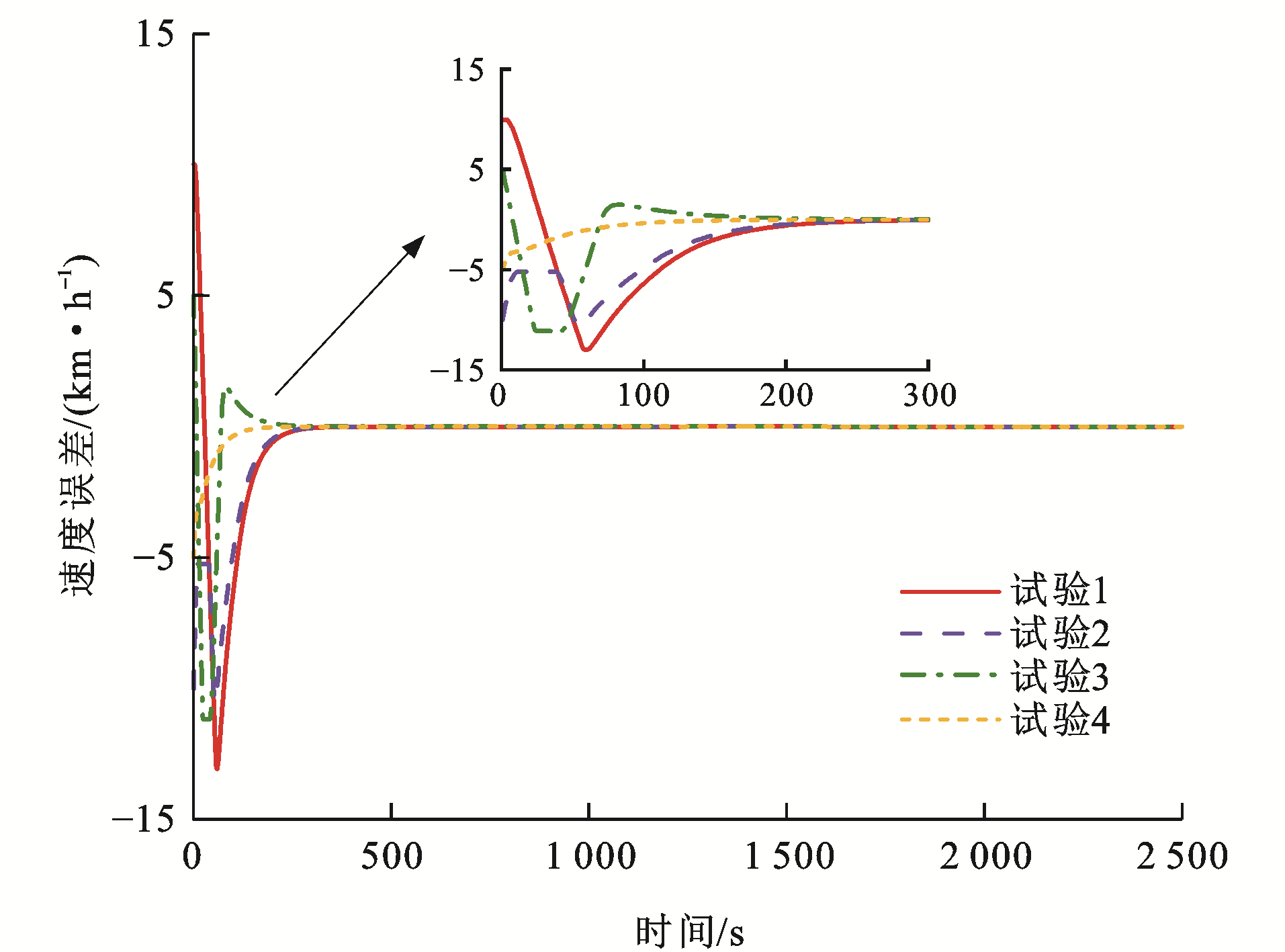
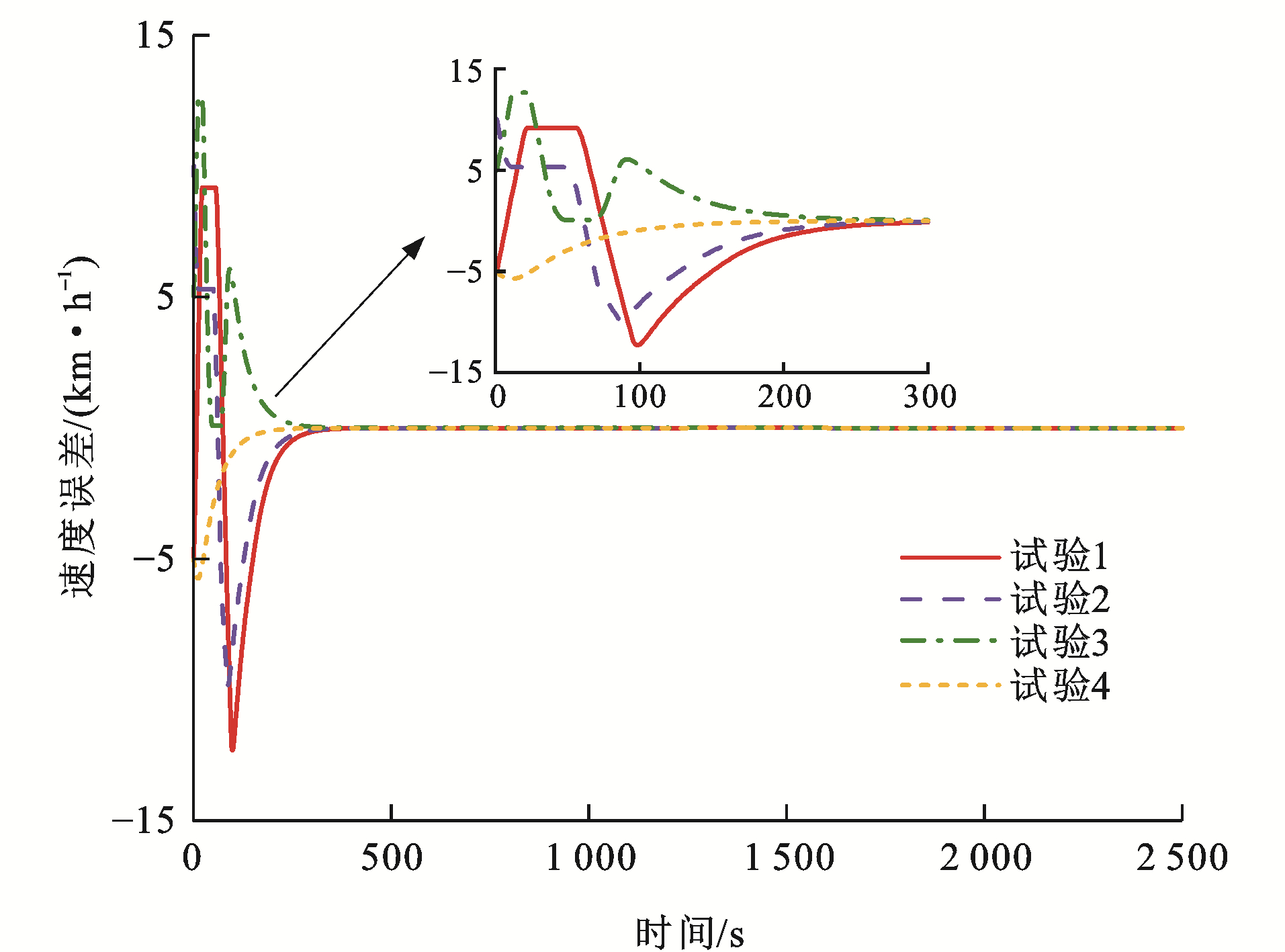
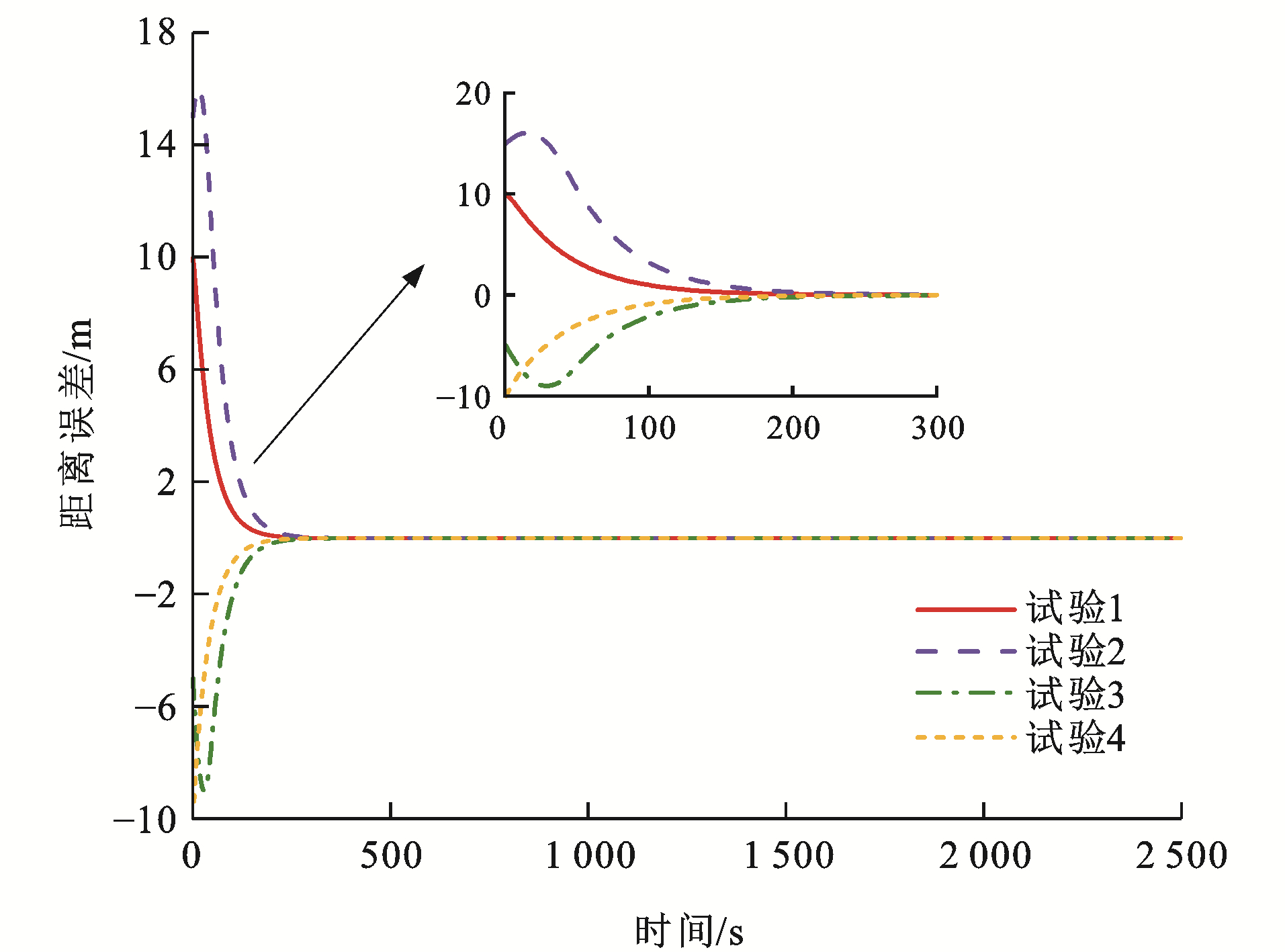
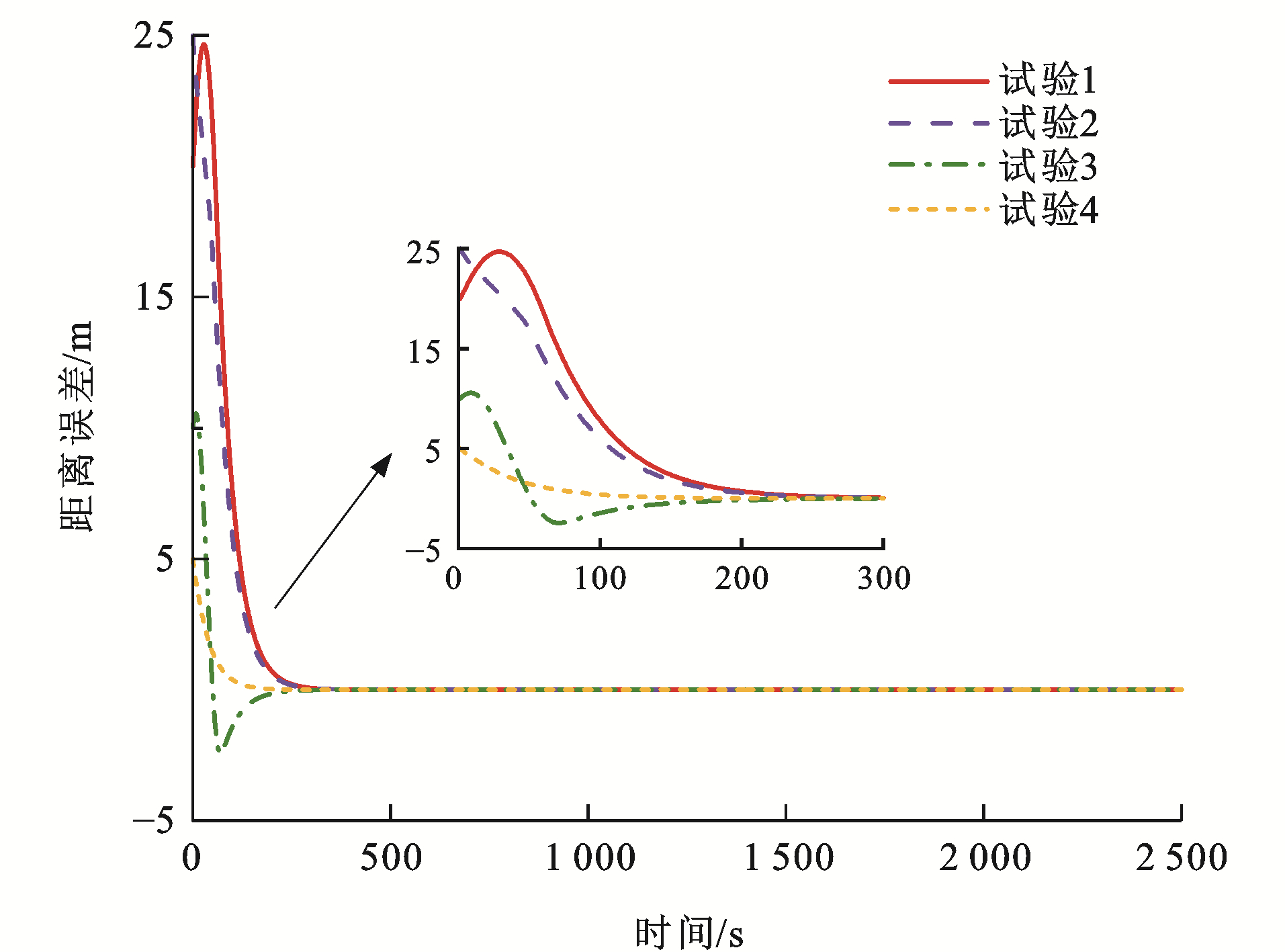
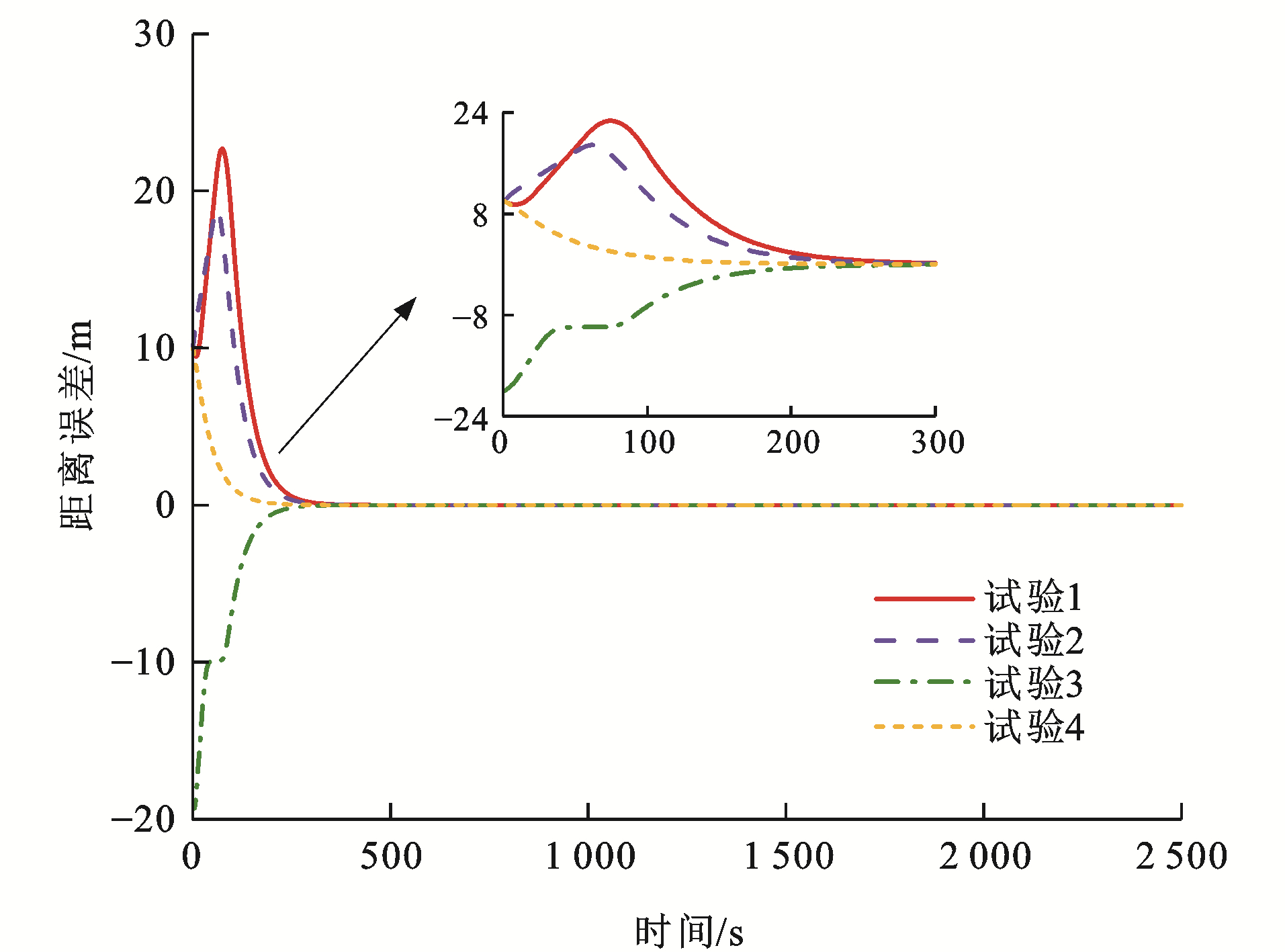
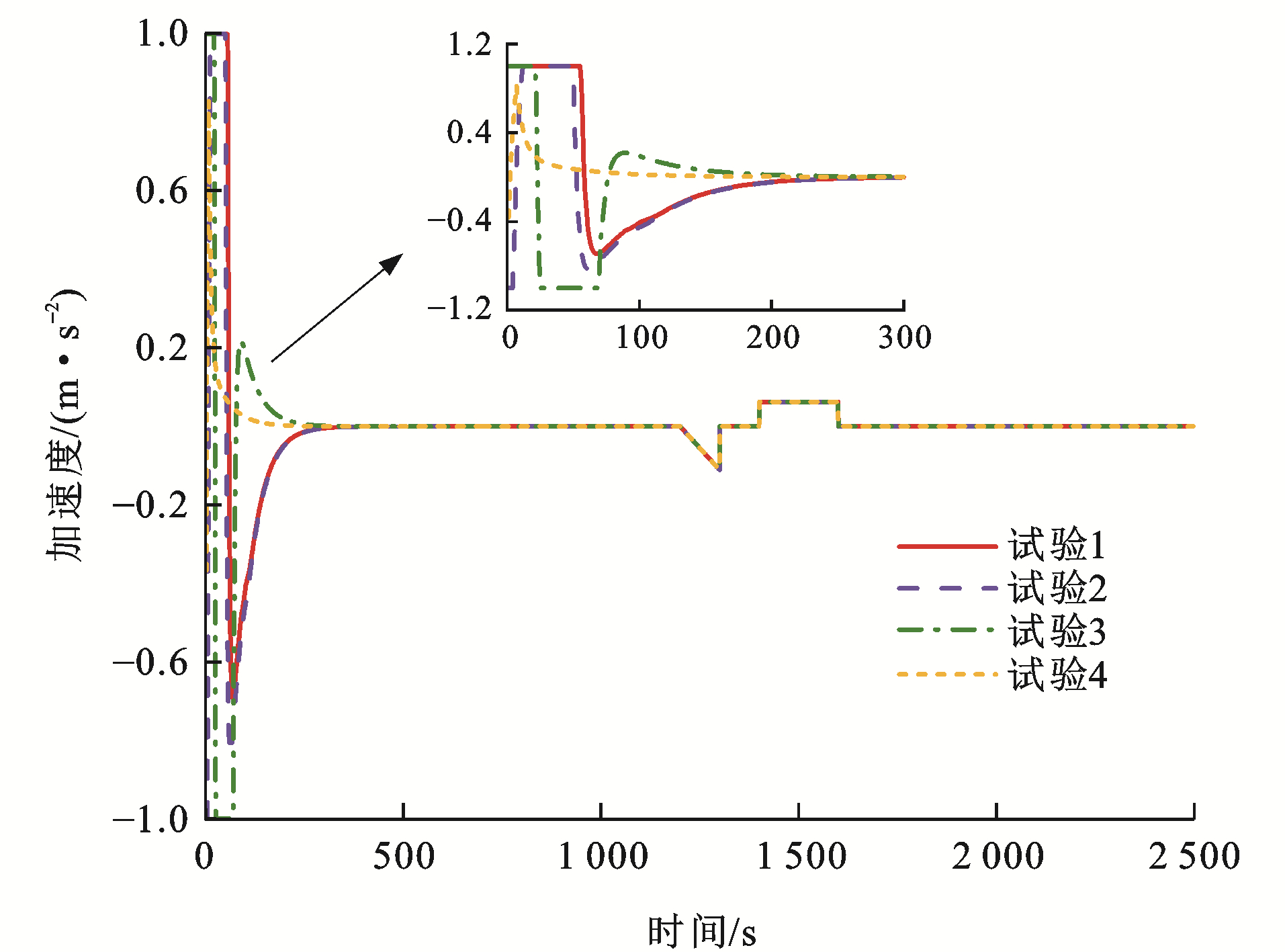
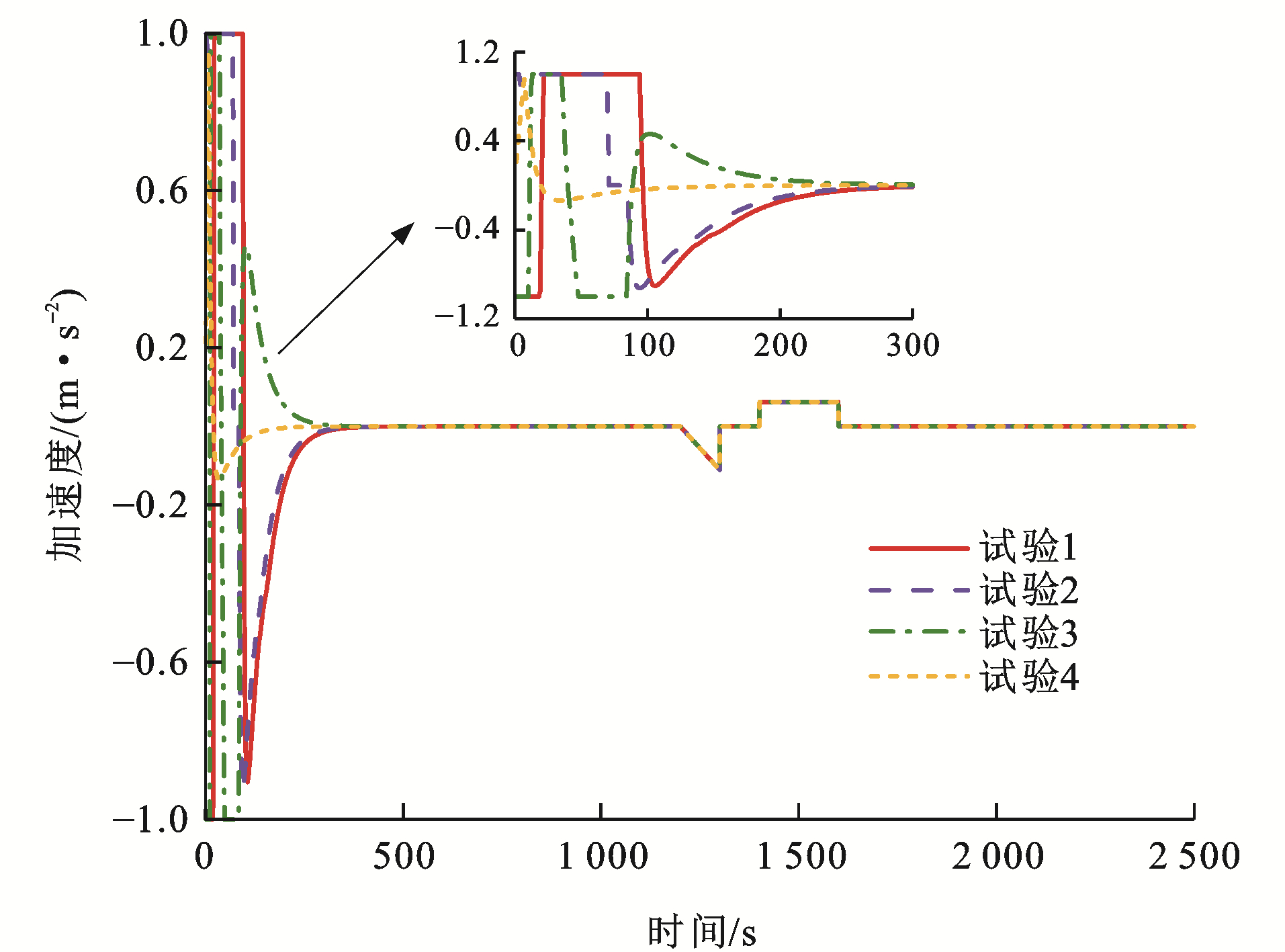
表 2 测试参数Table 2. Test parameters试验编号 初始速度误差/(km·h-1) 初始距离误差/m ev0, 1(0) ev1, 2(0) ev2, 3(0) es0, 1(0) es1, 2(0) es2, 3(0) 1 -5 10 -5 10 20 10 2 5 -10 10 15 25 10 3 -10 5 5 -5 10 -20 4 10 -5 -5 -10 5 10 图 8~13为各列车状态变化曲线，可以看出：对于4组试验，各列车之间的距离误差与速度误差均能在300 s后逐渐收敛至0，并一直处于稳定状态，这是非常高效且有效的。对于试验1，列车1的初始速度比列车0快5 km·h-1，列车3的初始速度比列车2同样快5 km·h-1，而列车2的初始速度比列车1慢10 km·h-1，并且由于4列单元列车之间的初始间距误差均大于0，为达到虚拟编组列车运行平衡状态，列车2有一个大幅度提升速度的过程，使得速度误差与间距误差急速下降，而后由于惯性作用需要减缓速度，使得队形平衡，由于列车2的急剧变化，使得列车3的速度误差曲线也会有较大变化；对于试验2，列车1的初始速度比列车0慢5 km·h-1, 列车3的初始速度比列车2慢10 km·h-1，而列车2的初始速度比列车1快10 km·h-1，4列单元列车之间的初始间距误差也均大于0，则列车1与列车3相对列车2而言，需要尽快提升速度以达到队形稳定，但列车2在稍微减缓速度之后也需提升速度，以缩短间距误差，因此，图 9中试验2的速度误差曲线会出现上升、下降、再上升的变化趋势；对于试验3，列车1的初始速度比列车0快10 km·h-1，而列车2的初始速度比列车1慢5 km·h-1，列车3的初始速度比列车2同样慢5 km·h-1，列车1与列车2之间的间距误差大于0，其余列车之间的间距误差均小于0，且|es0, 1(0)|<|es1, 2(0)|<|es2, 3(0)|，因此，列车1需尽快减缓速度以达队形稳定，列车2为缩短运行间距，应稍微提升速度，之后也需减缓速度，保证与前后车速度一致，而由于列车3的间距远小于理想间距，在列车2运行状态变化的影响下，为防止发生安全事故，列车3也应做出相应调整；对于试验4，列车1的初始速度比列车0慢10 km·h-1，而列车2的初始速度比列车1快5 km·h-1，列车3的初始速度比列车2同样快5 km·h-1，列车0与列车1的间距误差小于0，其余列车之间的间距误差均大于0，这种运行模式下，列车只需做出一些细微调整就能达成稳定队形，因此，各列车运行曲线变化较为平缓。
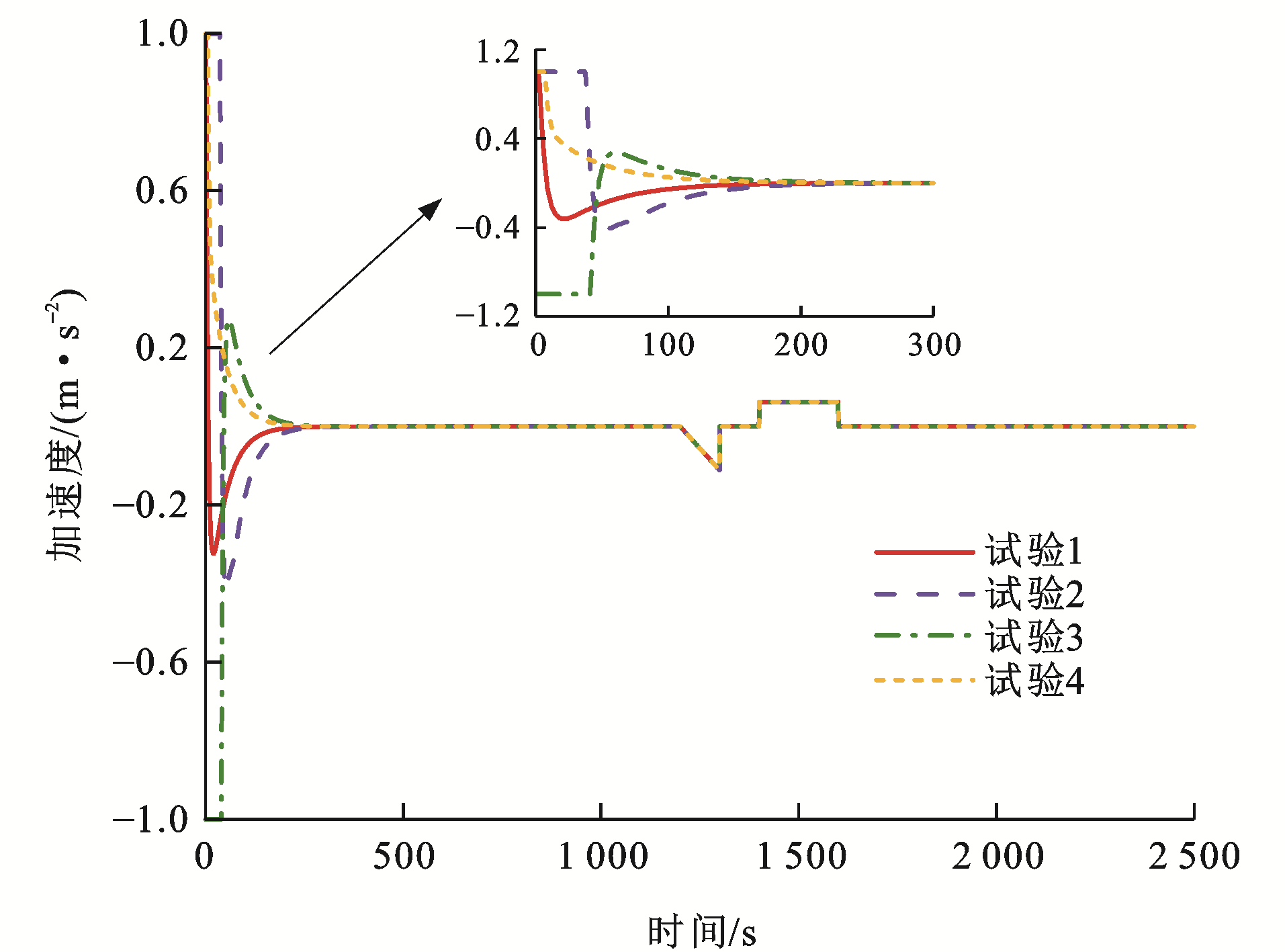
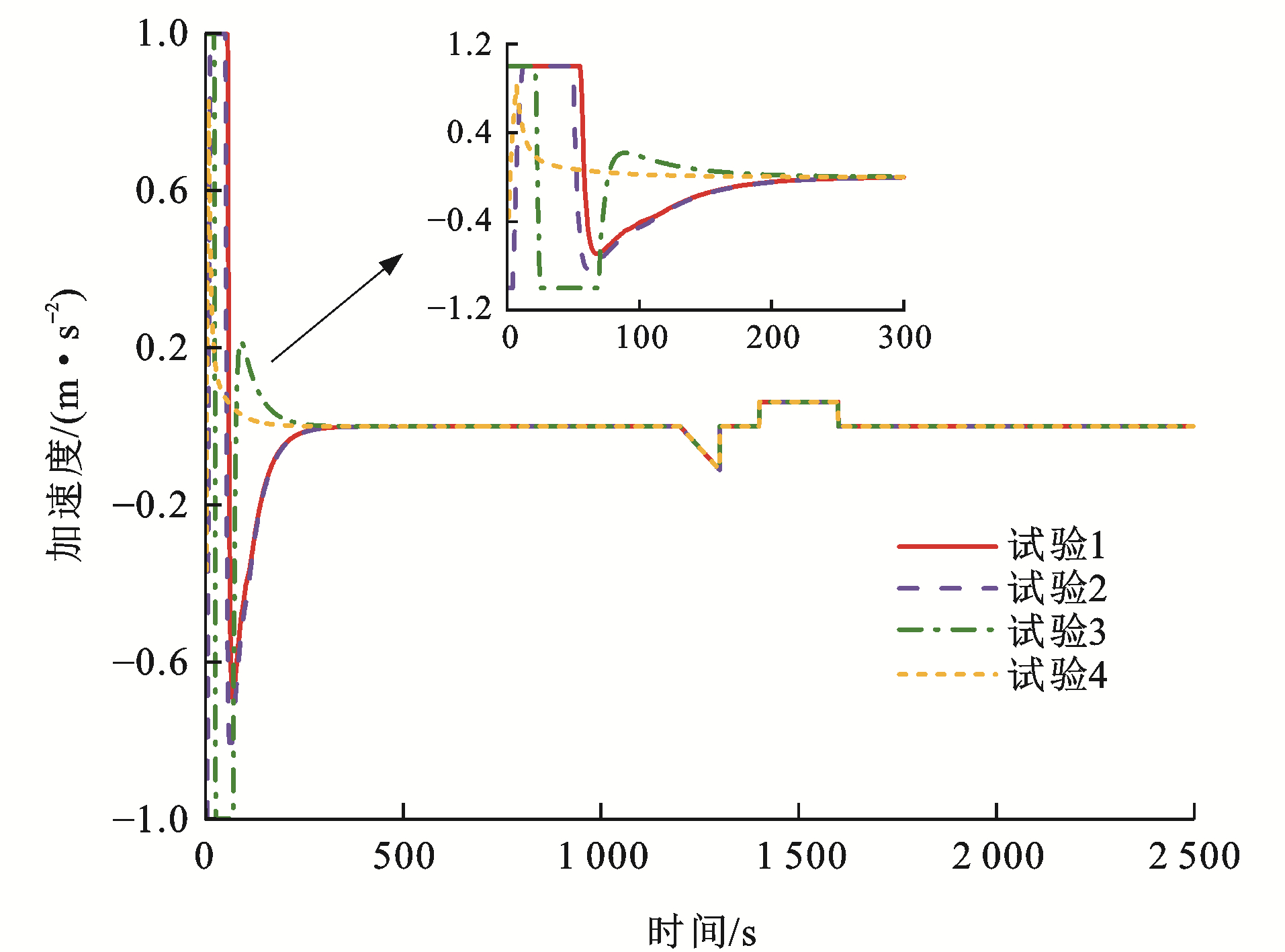
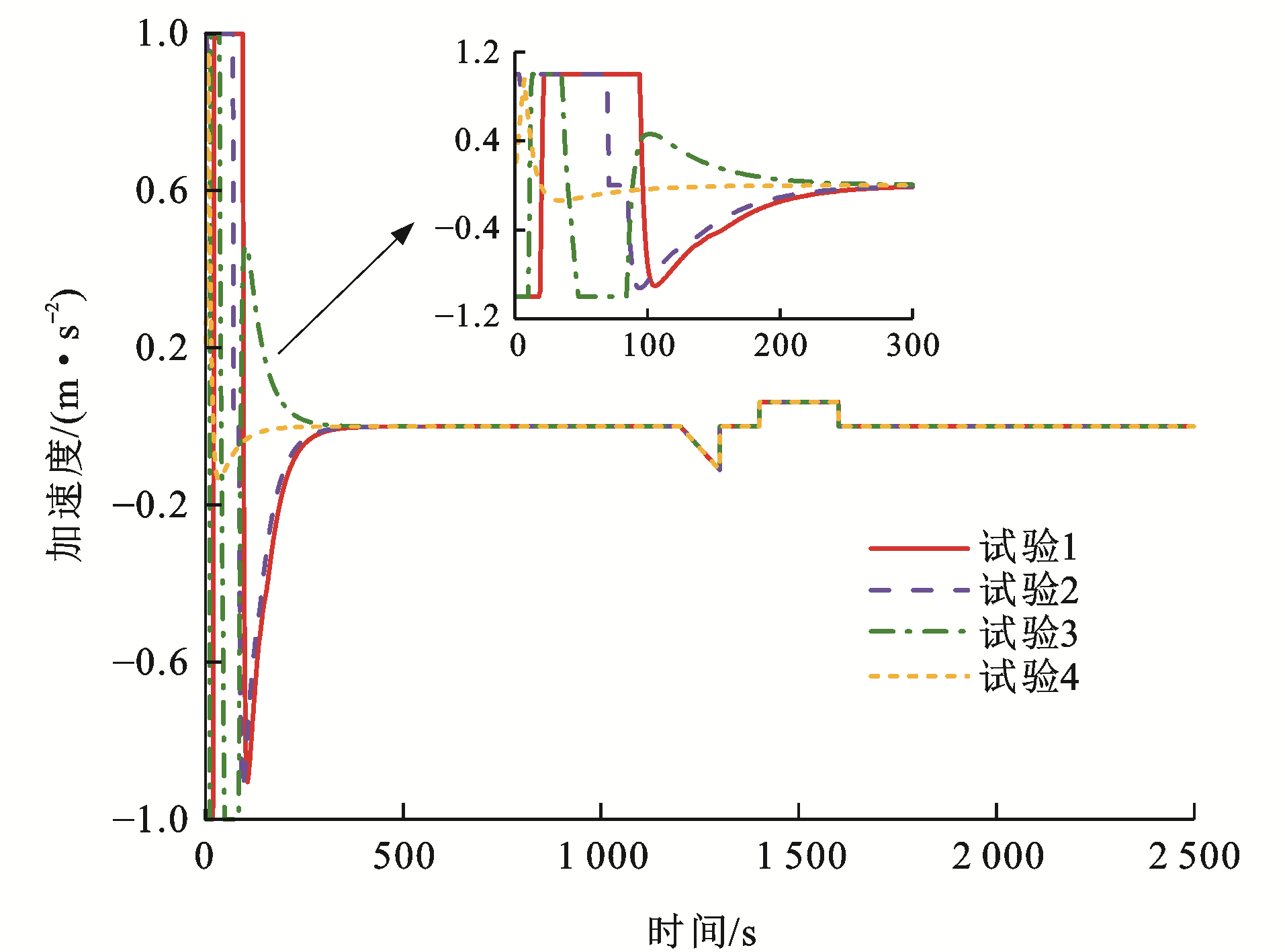
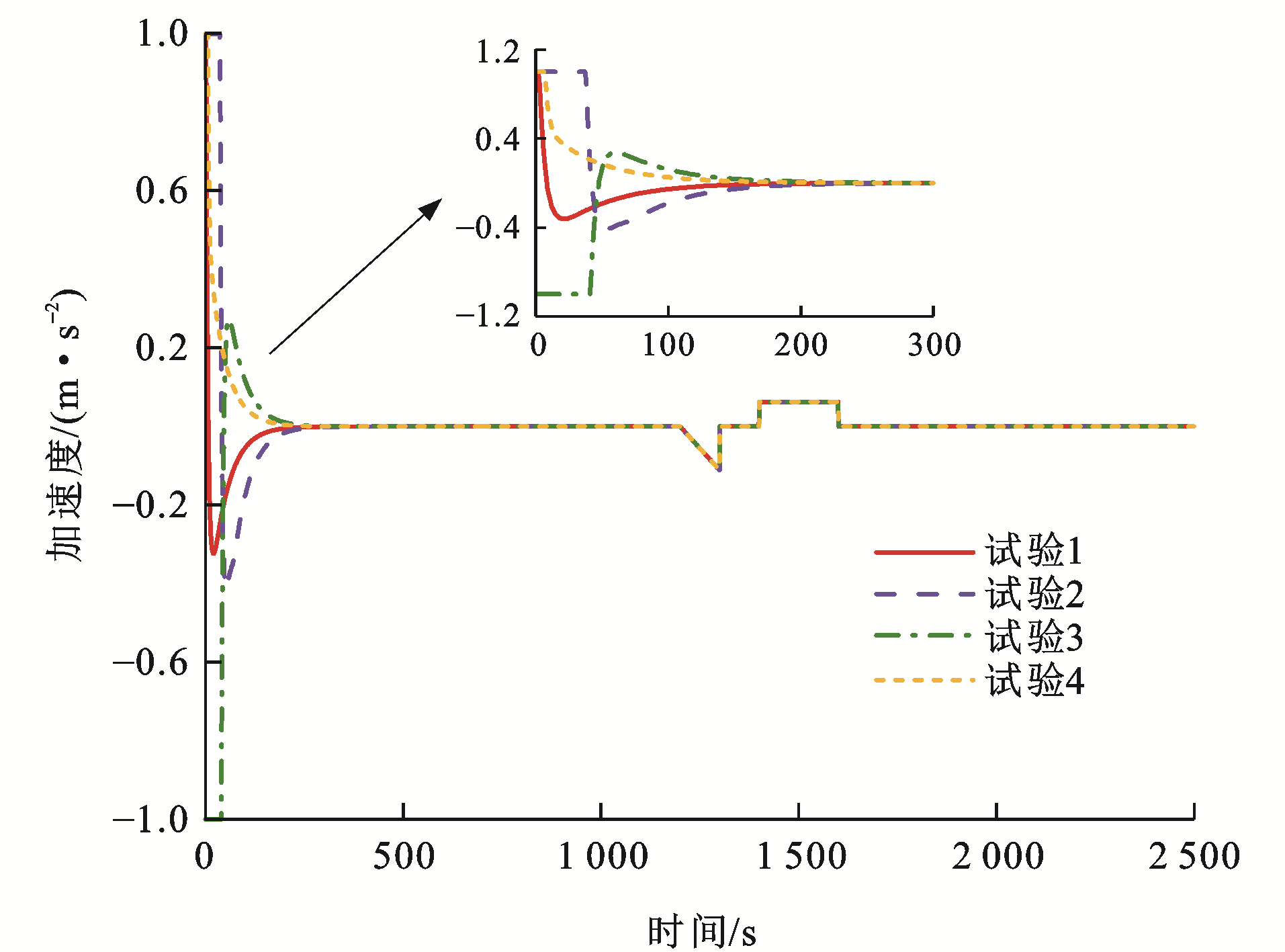
在图 14~16各组列车1~3的加速度曲线中，可以看出：在试验1中，处于编组阶段时列车2和3均采用最大加速度/最大减速度运行；在试验2中，列车1和3采用最大加速度提升列车运行速度，列车2先减缓速度后，开始以最大加速度提速；在试验3中，列车1采用最小加速度减缓列车运行速度，列车2提升速度后，开始以最大减速度减速，而列车3工况转换则较为频繁；在试验4中，各列车控制加速度变化较为平缓，且各组试验的控制加速度均保证在[-1, 1] m·s-2，满足了乘客舒适性要求；此外，在1 200 s左右，加速度有明显波动，这是因为设置的领导者列车0参考跟踪曲线的速度有所变化，从而导致跟随者列车的控制加速度会相应变化，以保证虚拟编组列车的稳定编队运行，在控制加速度的作用下，各单元列车的速度误差与间距误差均保持稳定。事实证明，在IMDMPC控制方法的控制作用下，列车能平稳高效地运行，验证了算法的稳定性，并且从各试验列车运行结果可以得出，在双向拓扑通信结构下列车运行耦合性较强，可在较快时间内实现列车的编队稳定运行。
表 3为4组试验各单元列车的初始状态信息与稳定后的状态信息，可以看到在不同初始状态条件下，列车队形均能达到稳定状态。
表 3 列车性能调整比较Table 3. Comparison of train performance adjustment试验编号 性能 初始状态 稳定状态 1 各单元列车速度/(km·h-1) v0(t) 280 280 v1(t) 285 280 v2(t) 275 280 v3(t) 280 280 各单元列车间距/m es0, 1(t) 110 100 es1, 2(t) 120 100 es2, 3(t) 110 100 2 各单元列车速度/(km·h-1) v0(t) 280 280 v1(t) 275 280 v2(t) 285 280 v3(t) 275 280 各单元列车间距/m es0, 1(t) 115 100 es1, 2(t) 125 100 es2, 3(t) 110 100 3 各单元列车速度/(km·h-1) v0(t) 280 280 v1(t) 290 280 v2(t) 285 280 v3(t) 280 280 各单元列车间距/m es0, 1(t) 95 100 es1, 2(t) 110 100 es2, 3(t) 80 100 4 各单元列车速度/(km·h-1) v0(t) 280 280 v1(t) 270 280 v2(t) 275 280 v3(t) 280 280 各单元列车间距/m es0, 1(t) 90 100 es1, 2(t) 105 100 es2, 3(t) 110 100 4.3 不同控制方法下仿真分析
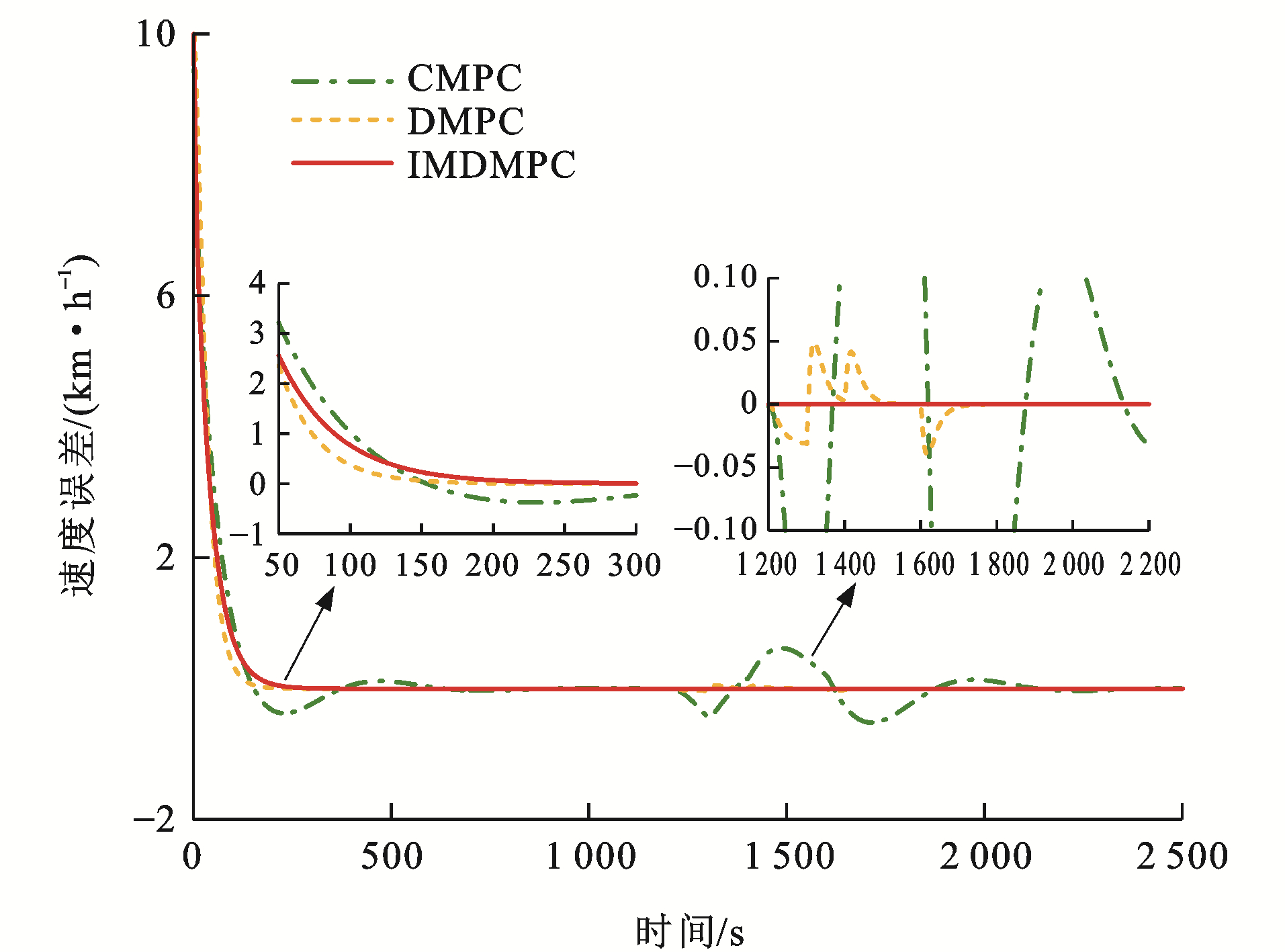
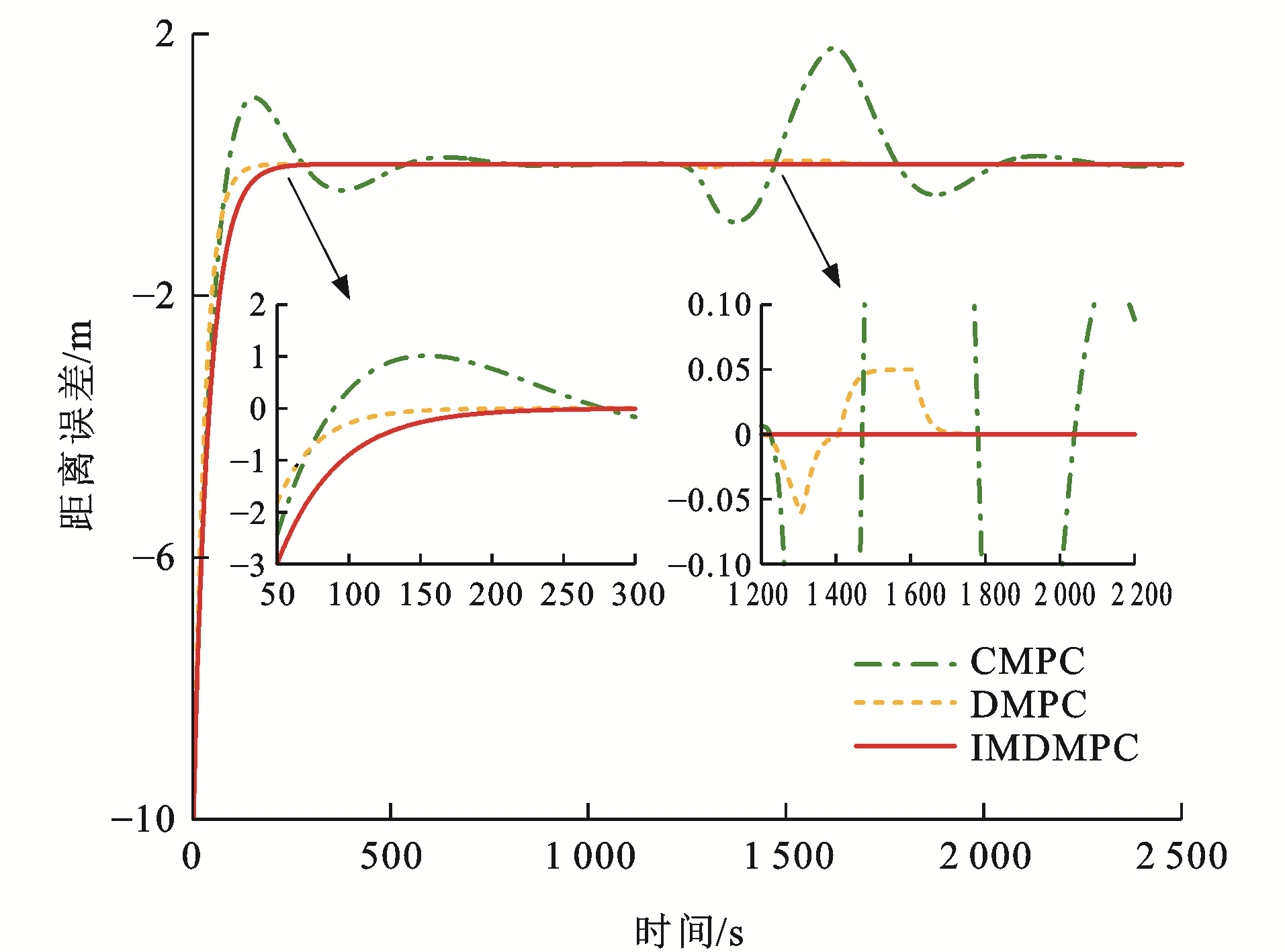
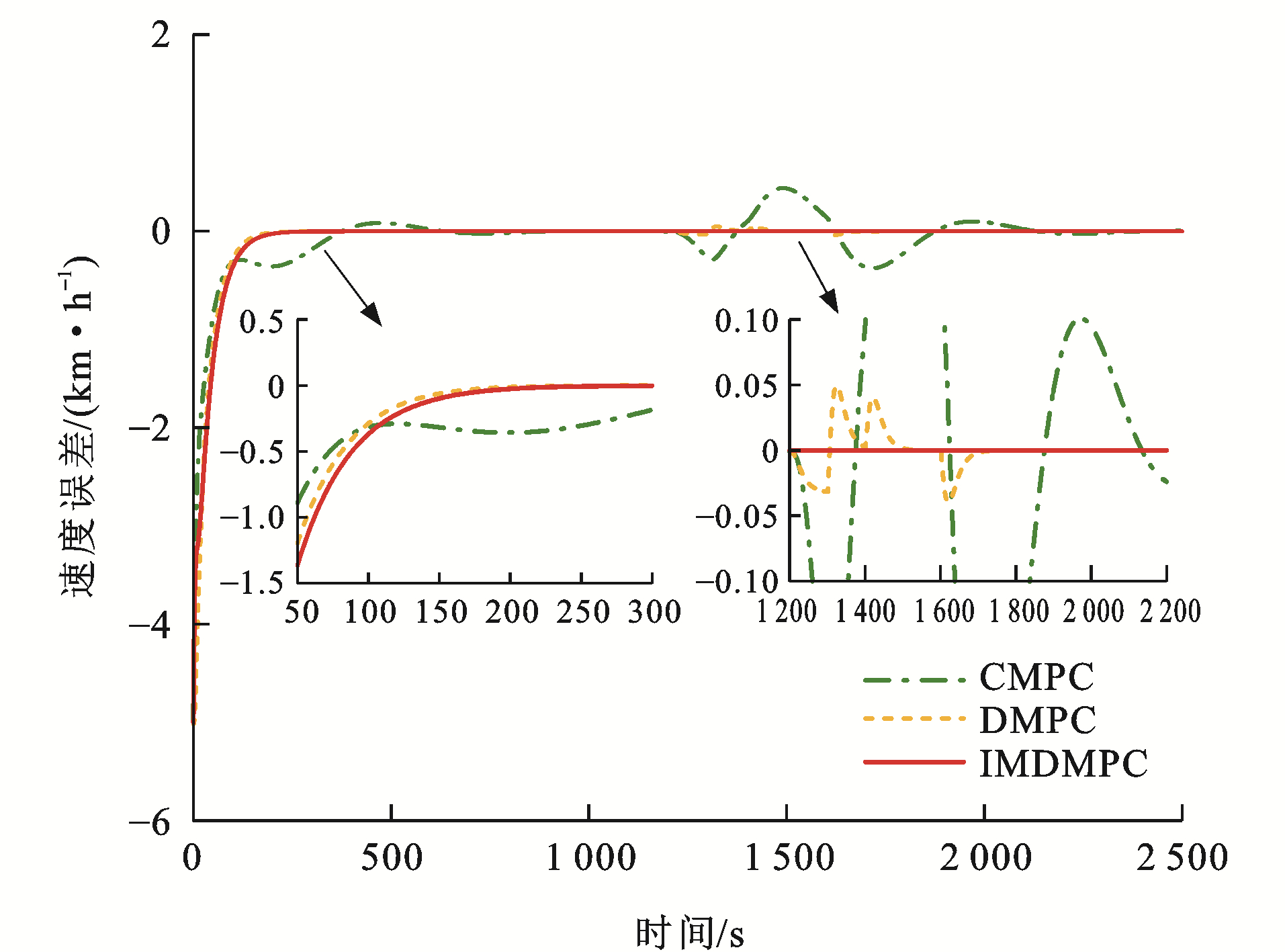
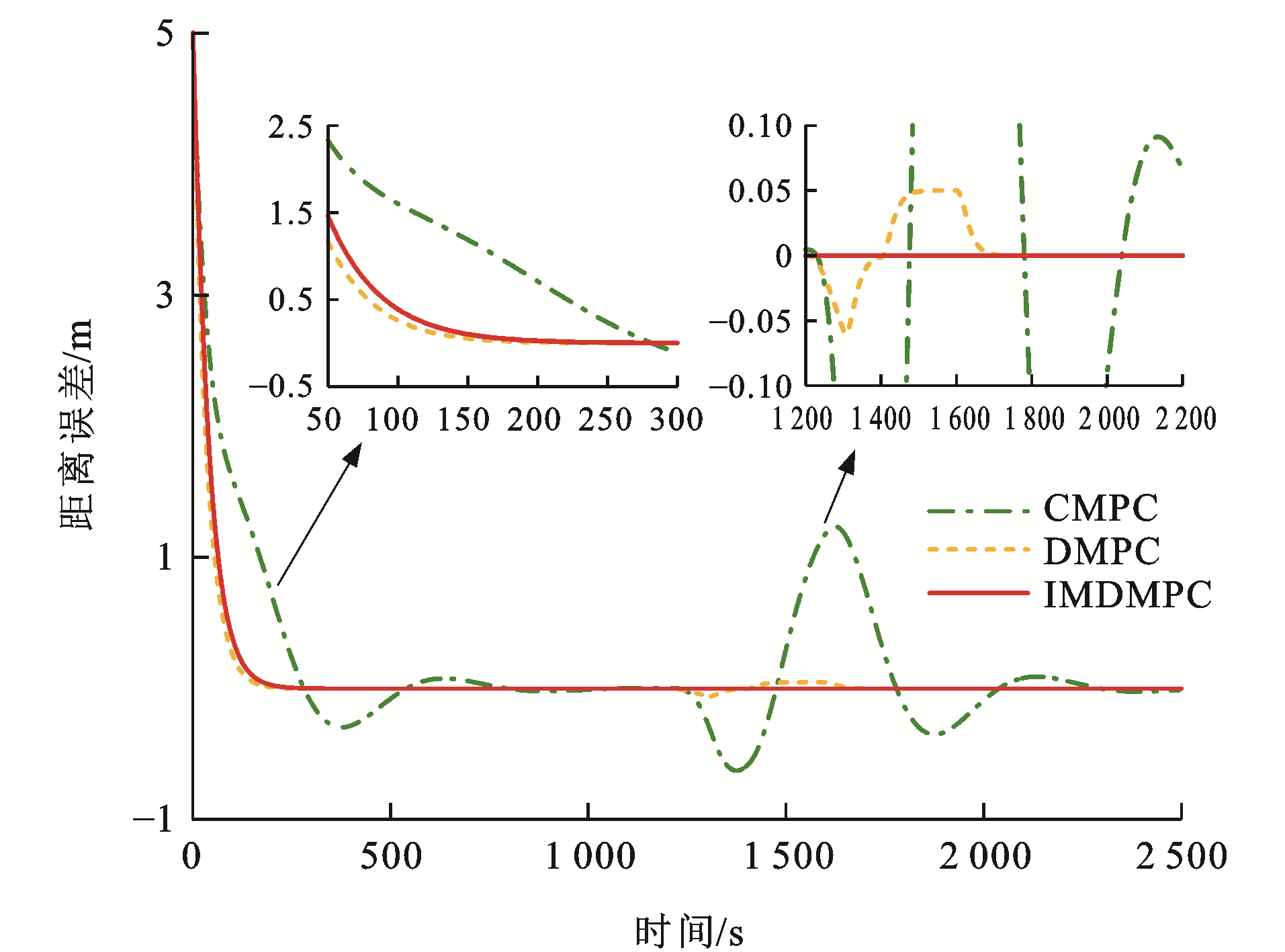
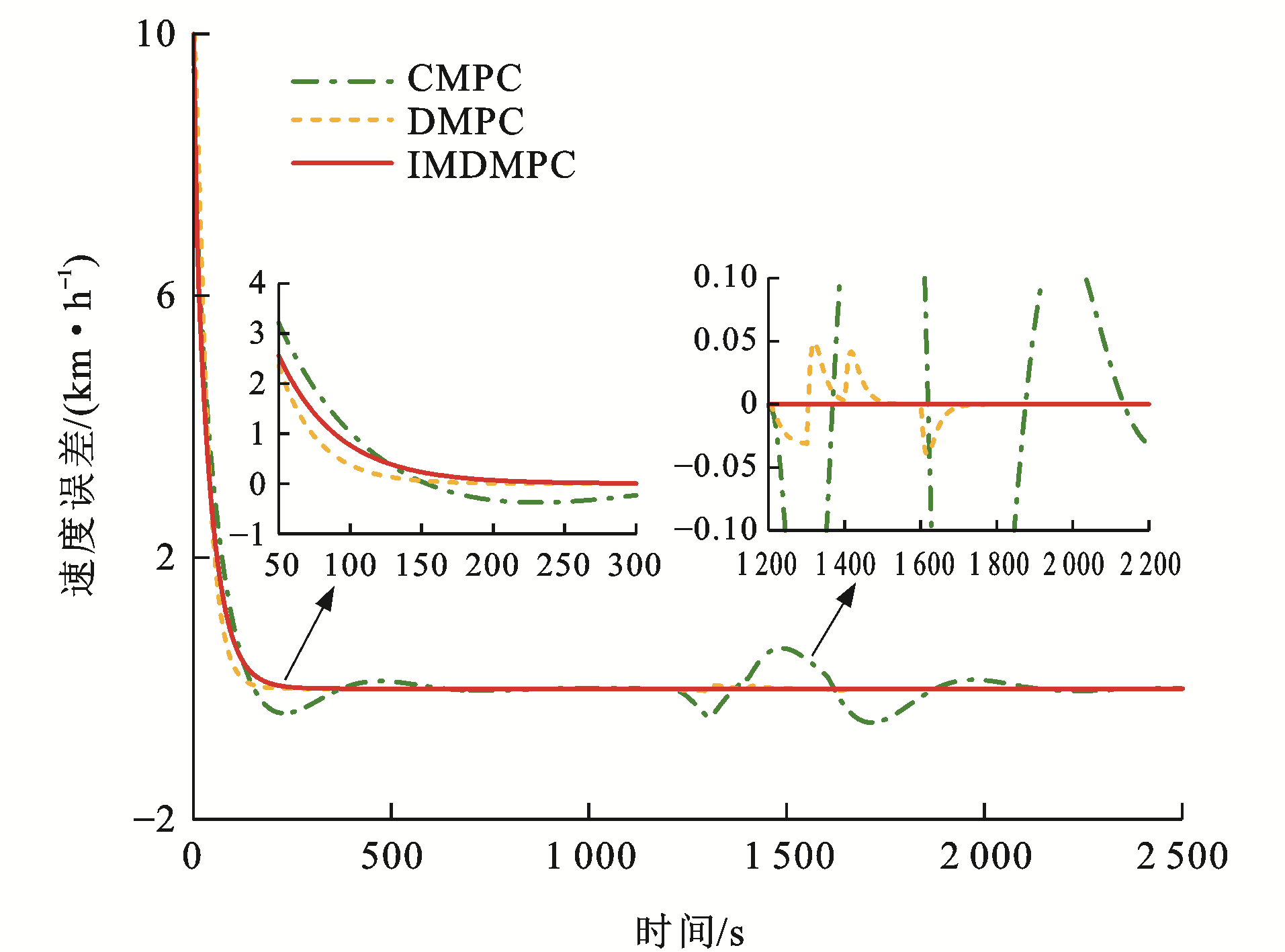
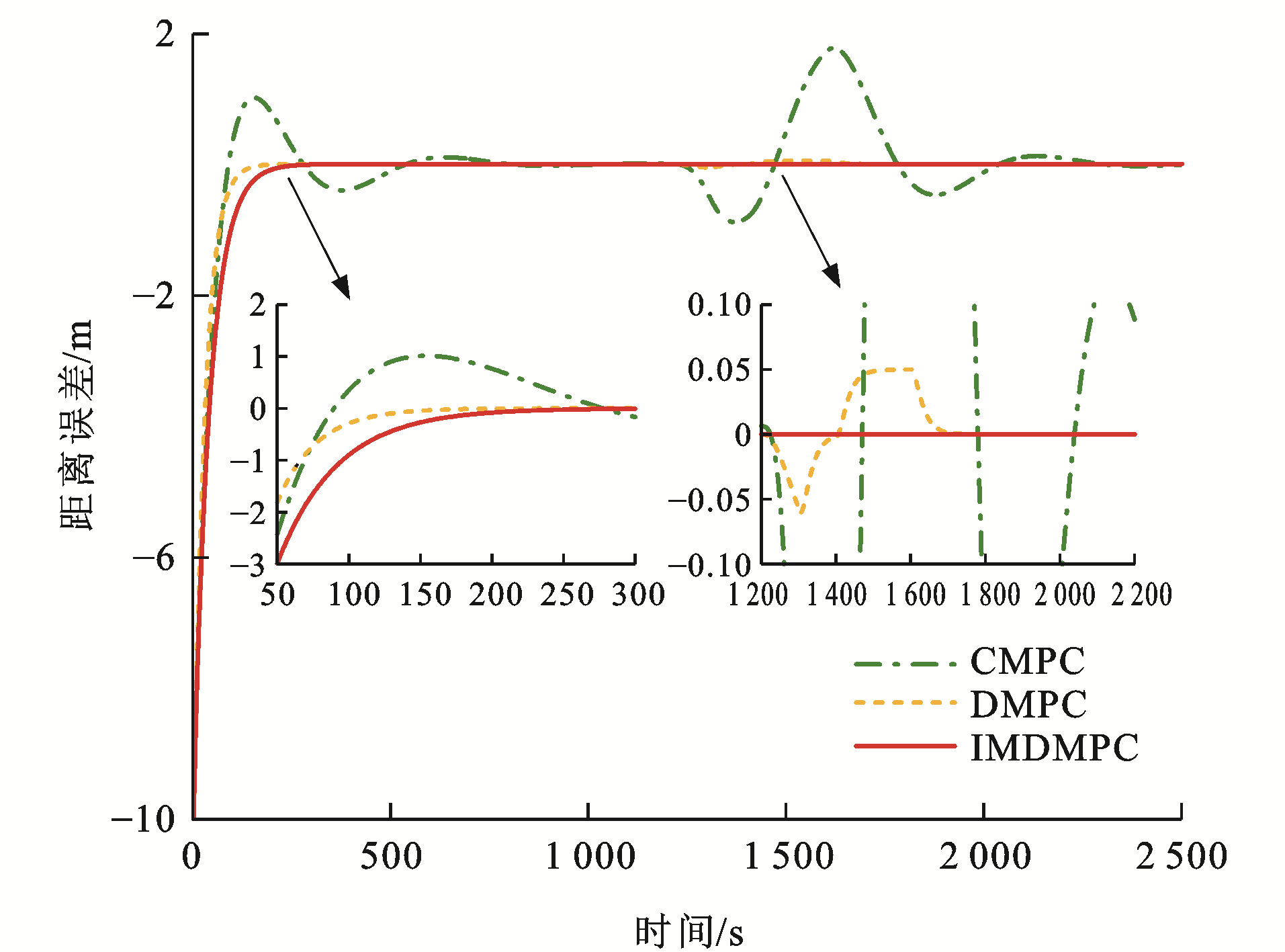
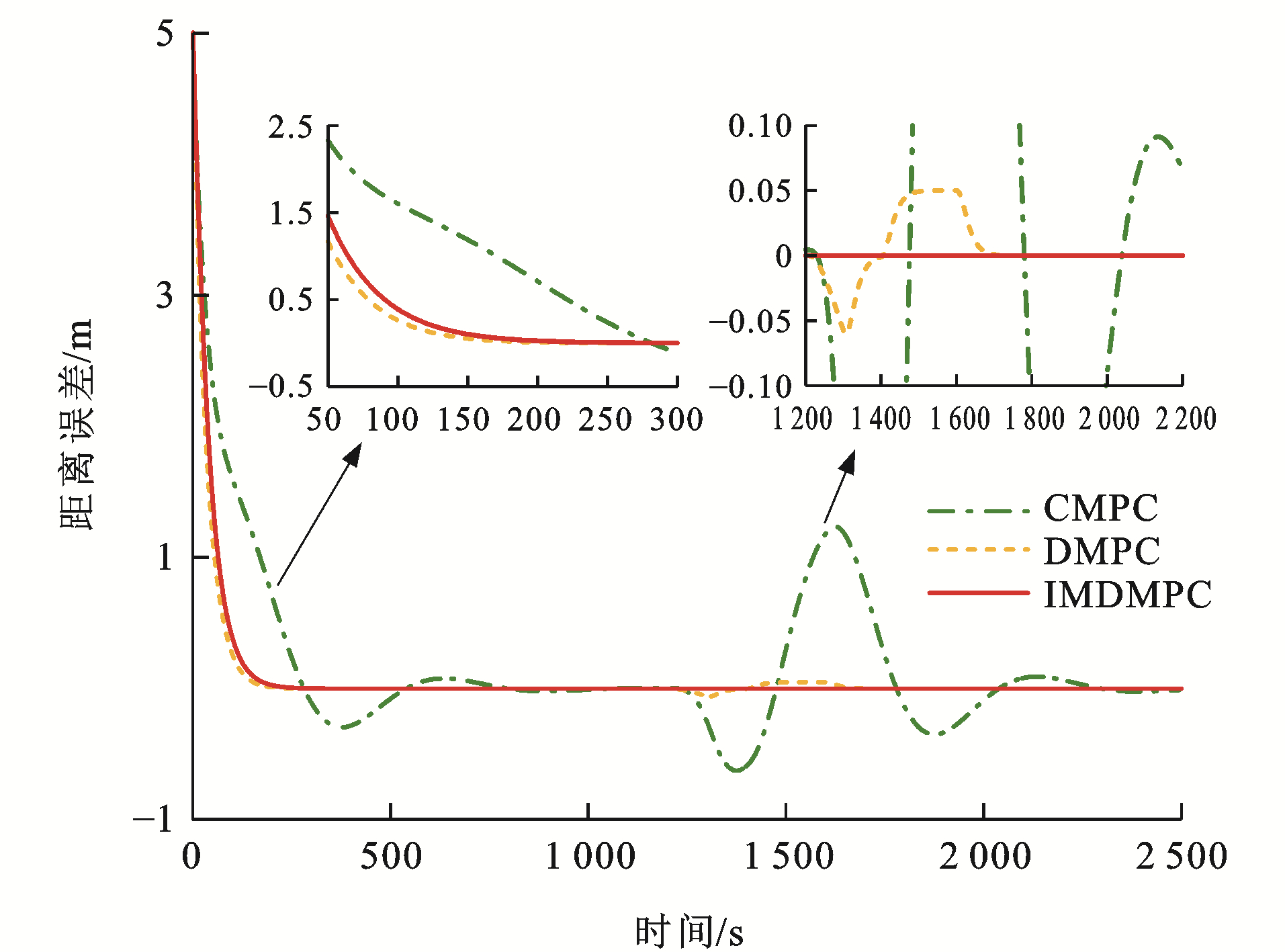
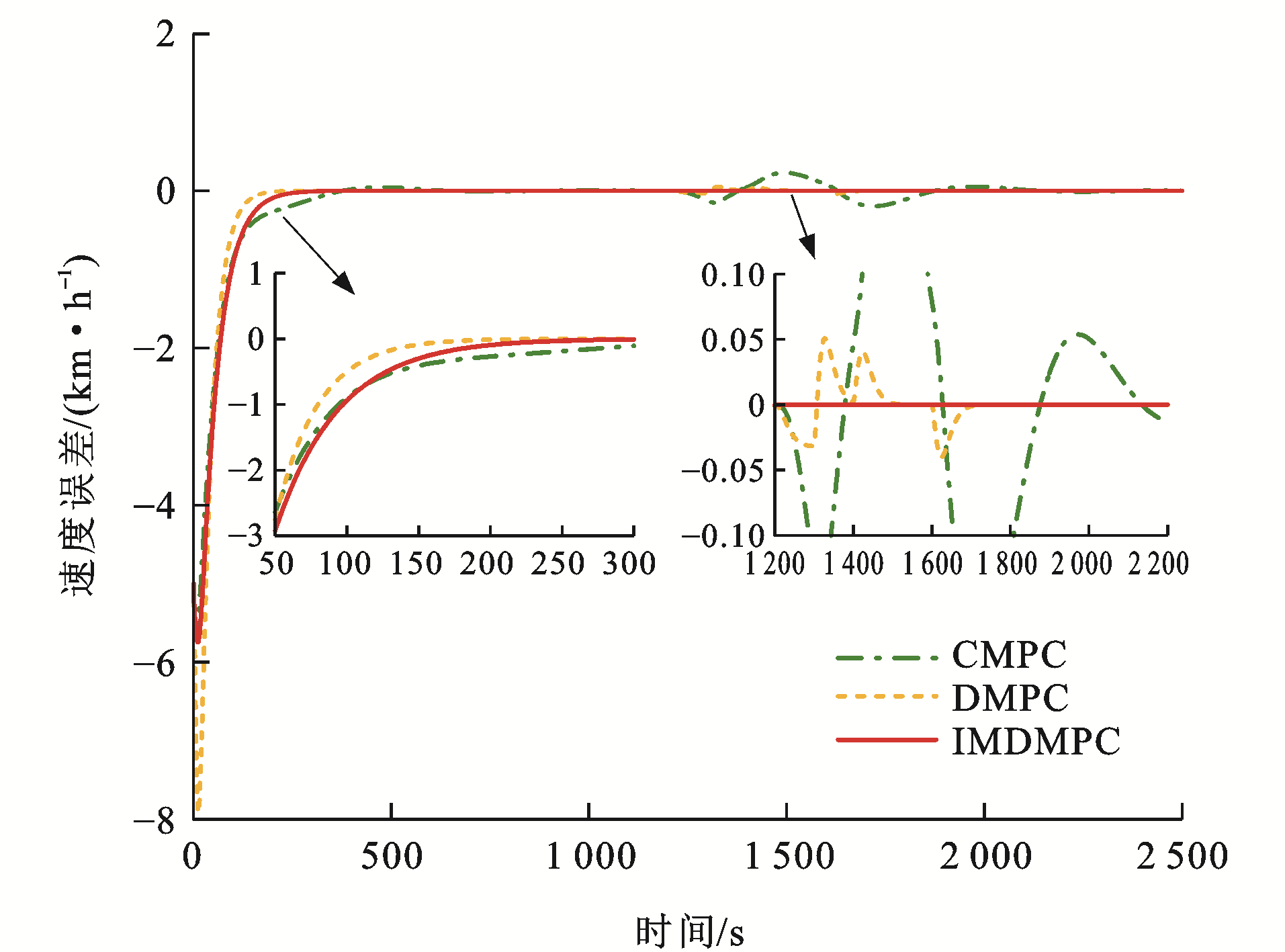
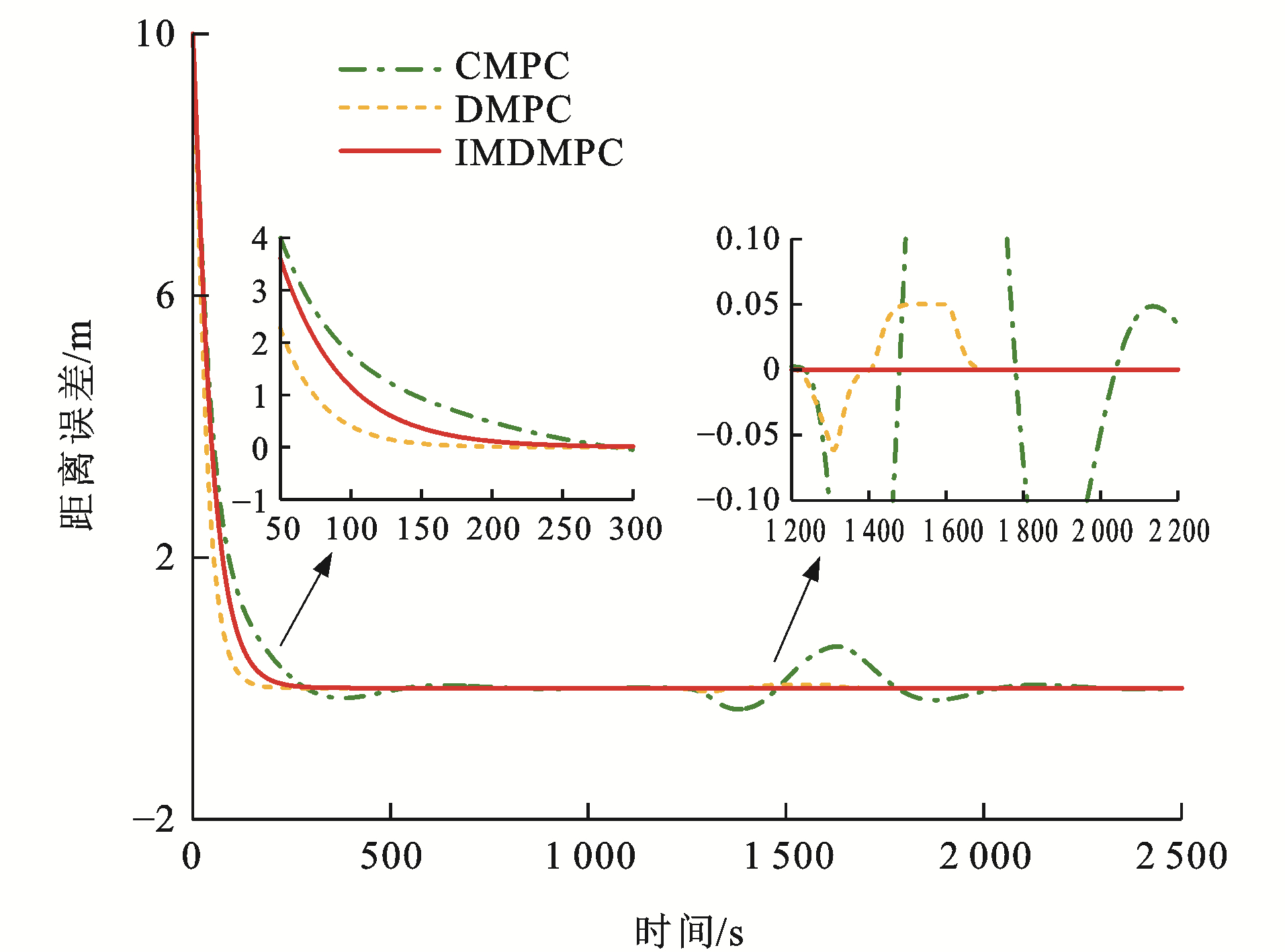
为了验证本文方法的优势，考虑在CMPC、传统DMPC[34]和改进DMPC(IMDMPC)这3种控制方法下进行仿真试验。采用4.2节中试验4的参数信息，对比3种方法的差异。
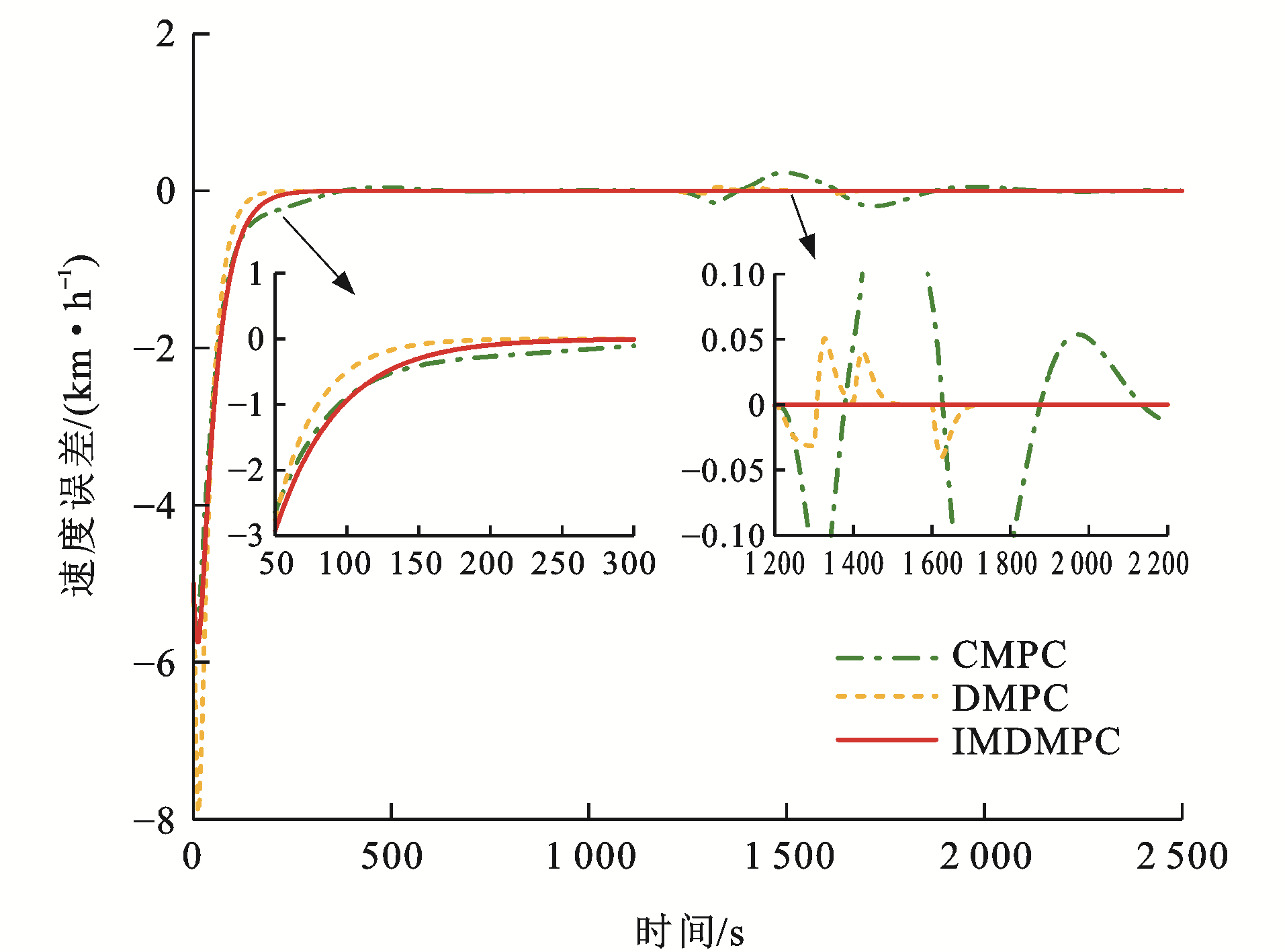
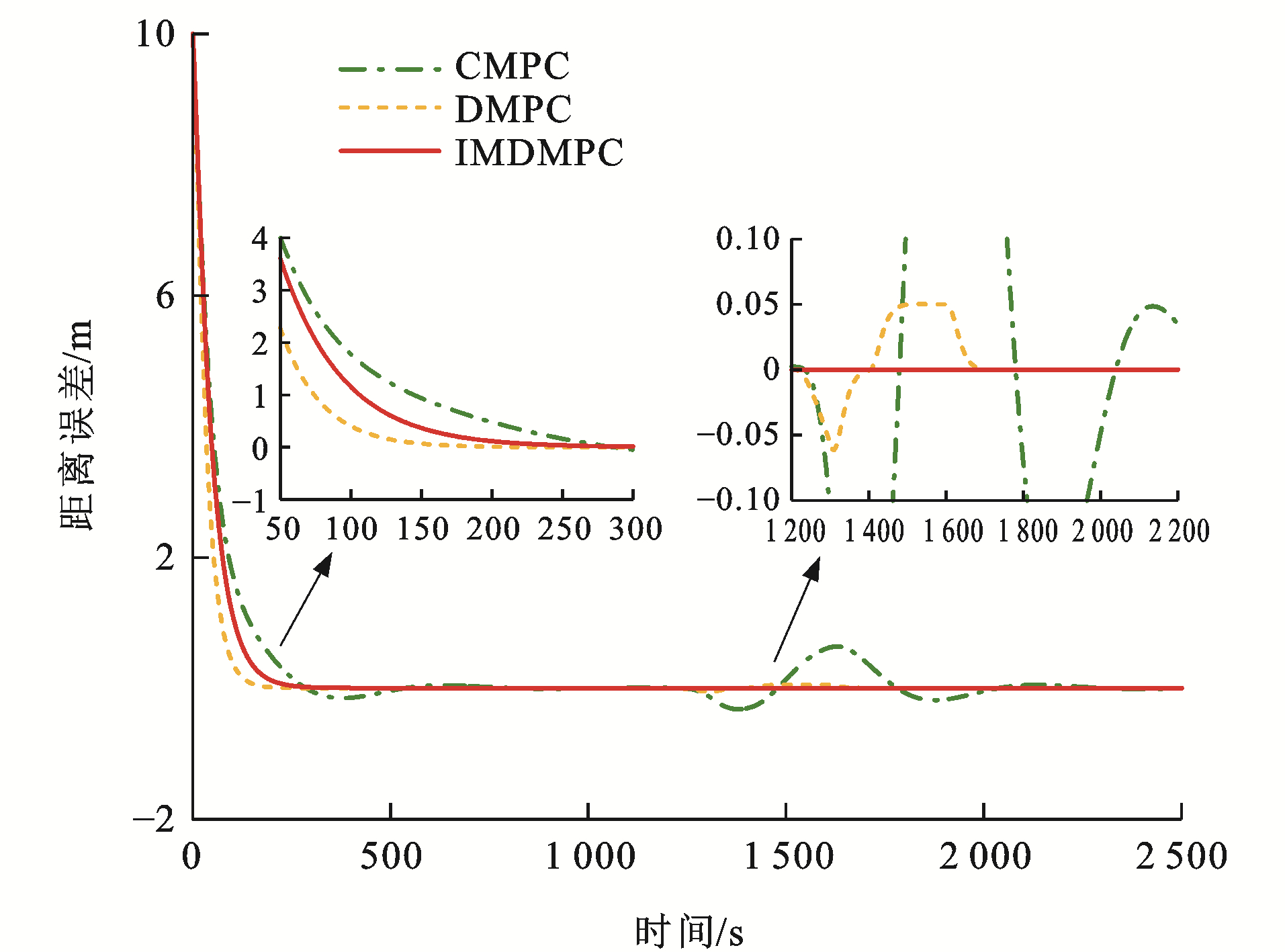
各控制算法下列车速度误差曲线和距离误差曲线分别见图 17~22，可以看出：与CMPC相比，IMDMPC控制方法下的状态曲线更加光滑，表明系统的平稳性得到了较大改善；与DMPC相比，IMDMPC下运行曲线误差更小，表明系统控制跟踪精度得到了提升；在1 200~2 200 s这个采样时间段内，领导者列车进行了3种工况调整，首先从惰性到制动，再到惰性，然后加速，再到惰性，显然CMPC和DMPC作用下的列车并不能及时调整队形，导致速度误差与距离误差波动较大；相比CMPC和DMPC，IMDMPC下的虚拟编组列车能迅速做出调整，保持队形的稳定，验证了算法的优势。
图 17 列车0与列车1速度误差对比Figure 17. Comparison of velocity errors between train 0 and train 1
图 18 列车0与列车1距离误差对比Figure 18. Comparison of distance errors between train 0 and train 1
图 19 列车1与列车2速度误差对比Figure 19. Comparison of velocity errors between train 1 and train 2
图 20 列车1与列车2距离误差对比Figure 20. Comparison of distance errors between train 1 and train 2
图 21 列车2与列车3速度误差对比Figure 21. Comparison of velocity errors between train 2 and train 3
图 22 列车2与列车3距离误差对比Figure 22. Comparison of distance errors between train 2 and train 3为了更为直观地分析各控制算法的控制性能，根据式(41)、(42)和(43)分别计算各控制器的速度均方根误差Mev、距离均方根误差Mes及能量损耗W[35]为
\left.M_{\mathrm{ev}}=\frac{1}{I T} \sum\limits_{i=1}^I \sum\limits_{t=1}^T \right\rvert\, e_{v_{i, i-1}}(t) (41) M_{\mathrm{es}}=\frac{1}{I T} \sum\limits_{i=1}^I \sum\limits_{t=1}^T\left|e_{s_{i, i-1}}(t)\right| (42) W=\sum\limits_{i=1}^I \sum\limits_{t=1}^T u_i^2(t) (43) 以采样时间T=300 s往后计算其均方根误差，表 4为3种控制算法的性能指标，均方根误差指标越小，说明系统跟踪效果越精确，控制算法越好。在[0, 300] s这个采样范围内，CMPC的均方根误差会小于DMPC的均方根误差，这是因为CMPC采用集中式控制策略，计算4列单元列车整体的误差最小值，而DMPC则根据前列列车的运行状态计算最优控制量进行实时调整本单元列车，因此，IMDMPC具有更好的优越性。
表 4 算法性能指标对比Table 4. Comparison of algorithm performance indexes算法 Mev/(km·h-1) Mes/m W/(m2·s-4) CMPC 1.08×10-3 0.140 2 5.959 2 DMPC 8.12×10-6 2.80×10-4 3.772 5 IMDMPC 3.32×10-8 6.11×10-7 3.579 4 4.4 控制结构输出时间仿真分析
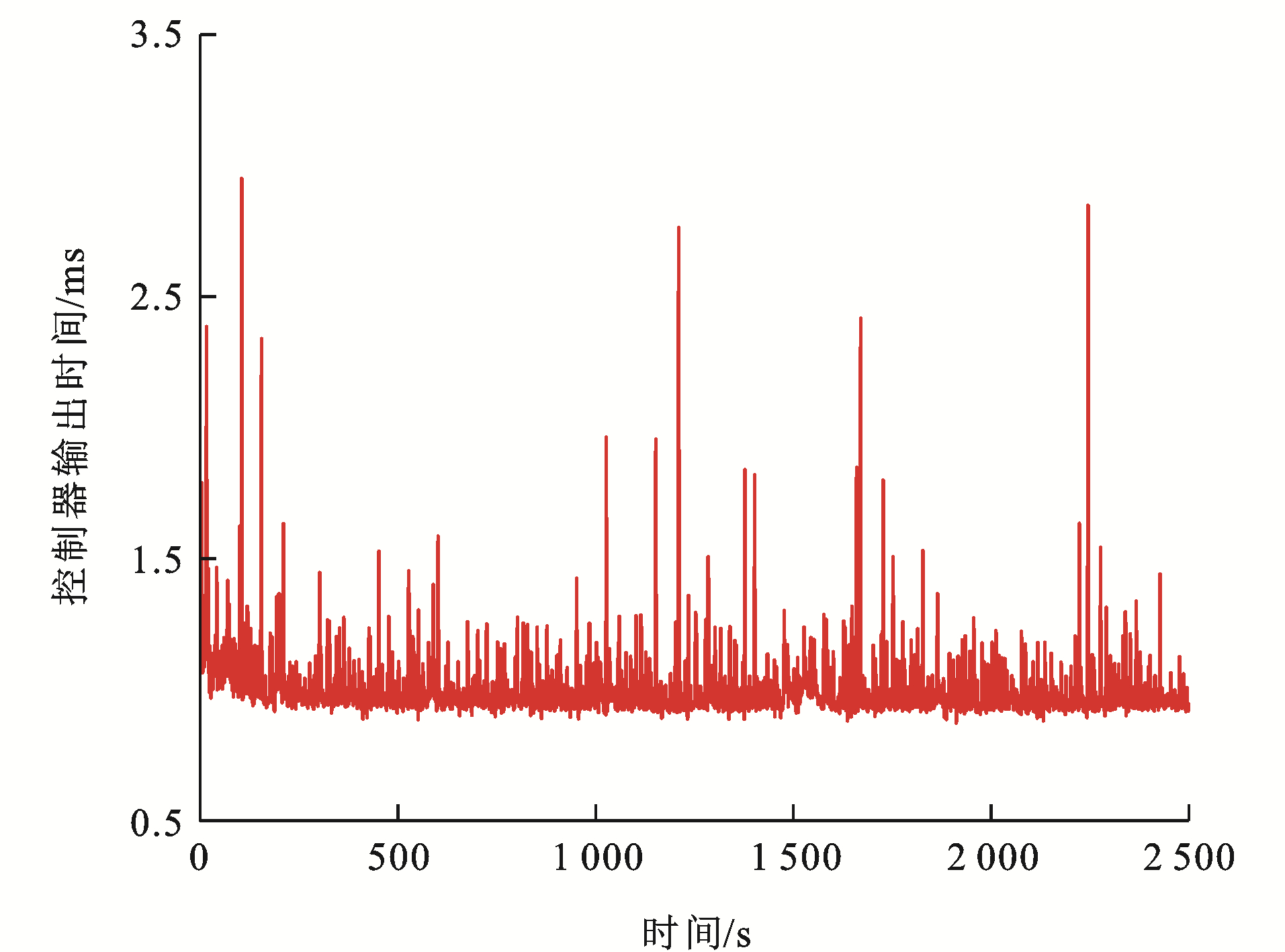
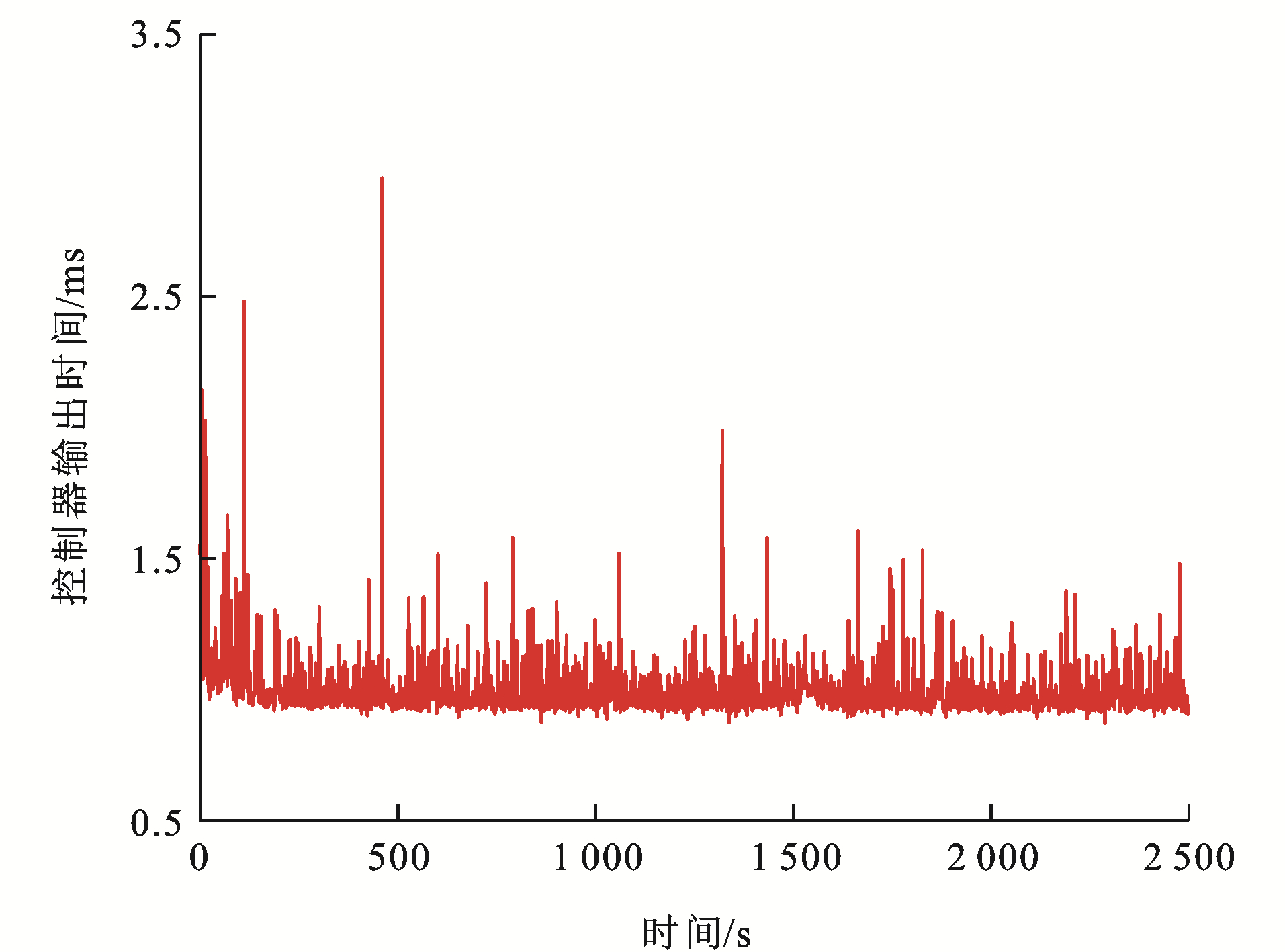
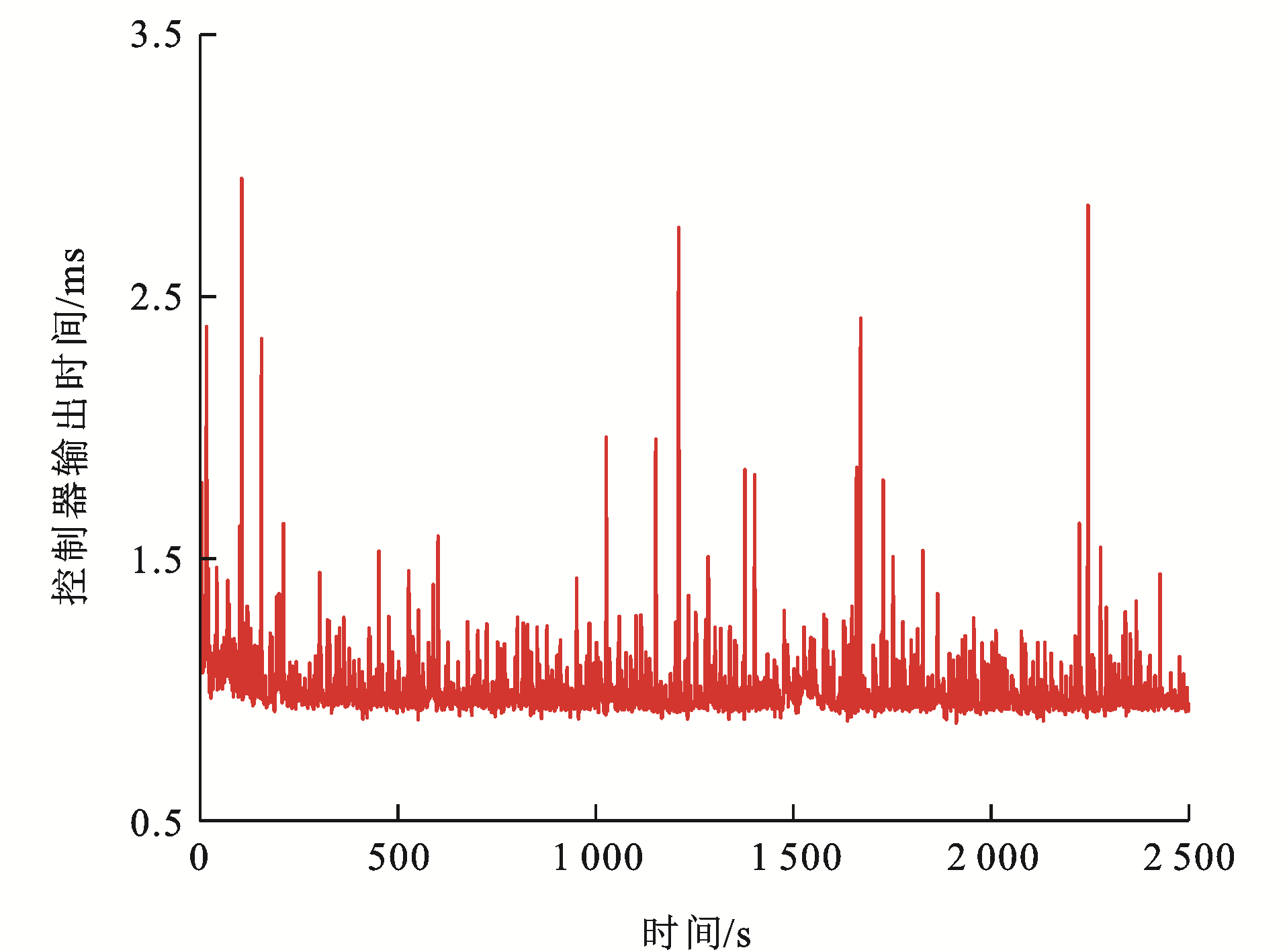
为了验证本文方法的实时性，对控制结构的输出时间进行仿真分析。同样采用4.2节中试验4的参数信息分析各单元列车控制器采样时刻的计算仿真时长。
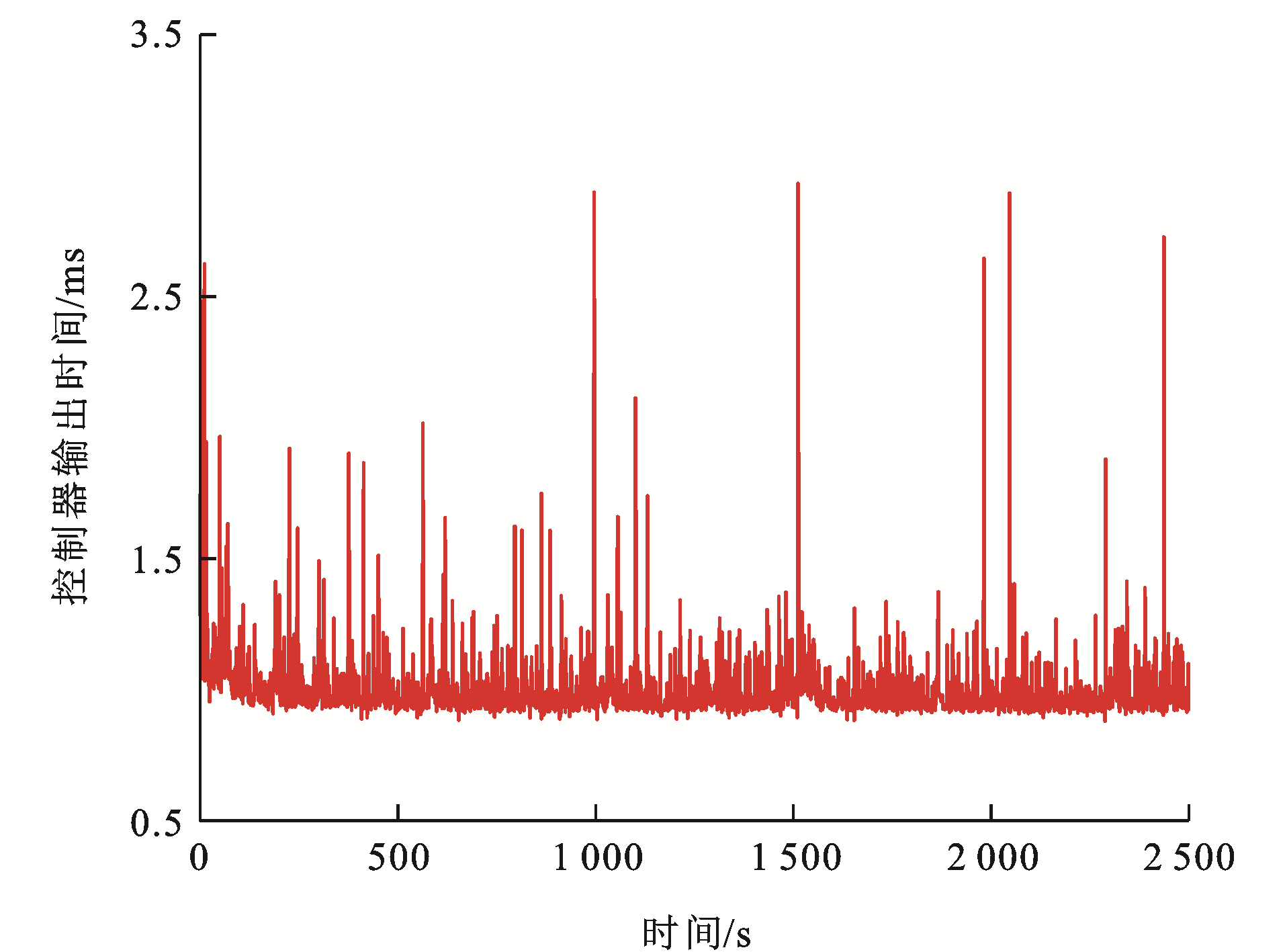
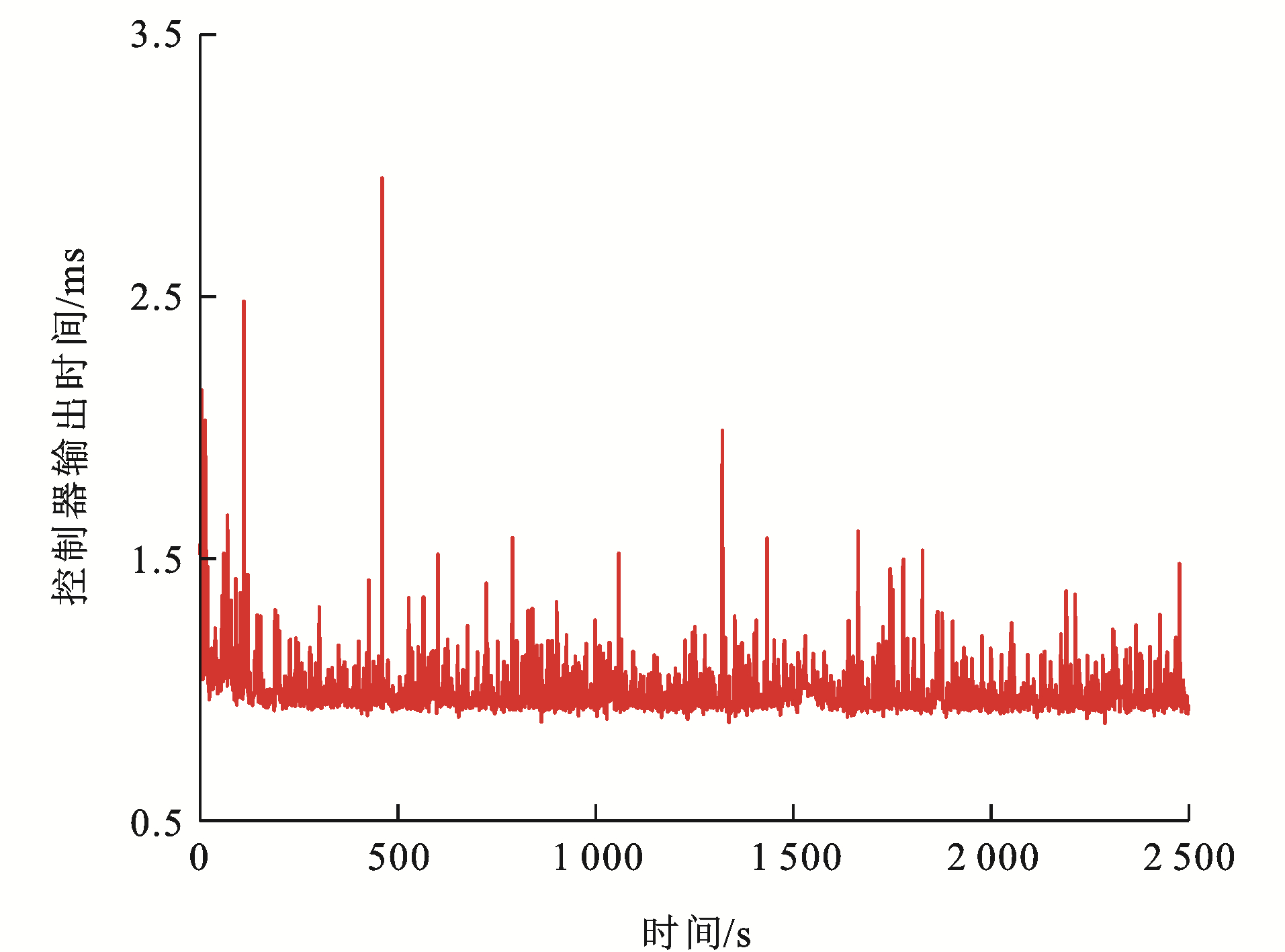
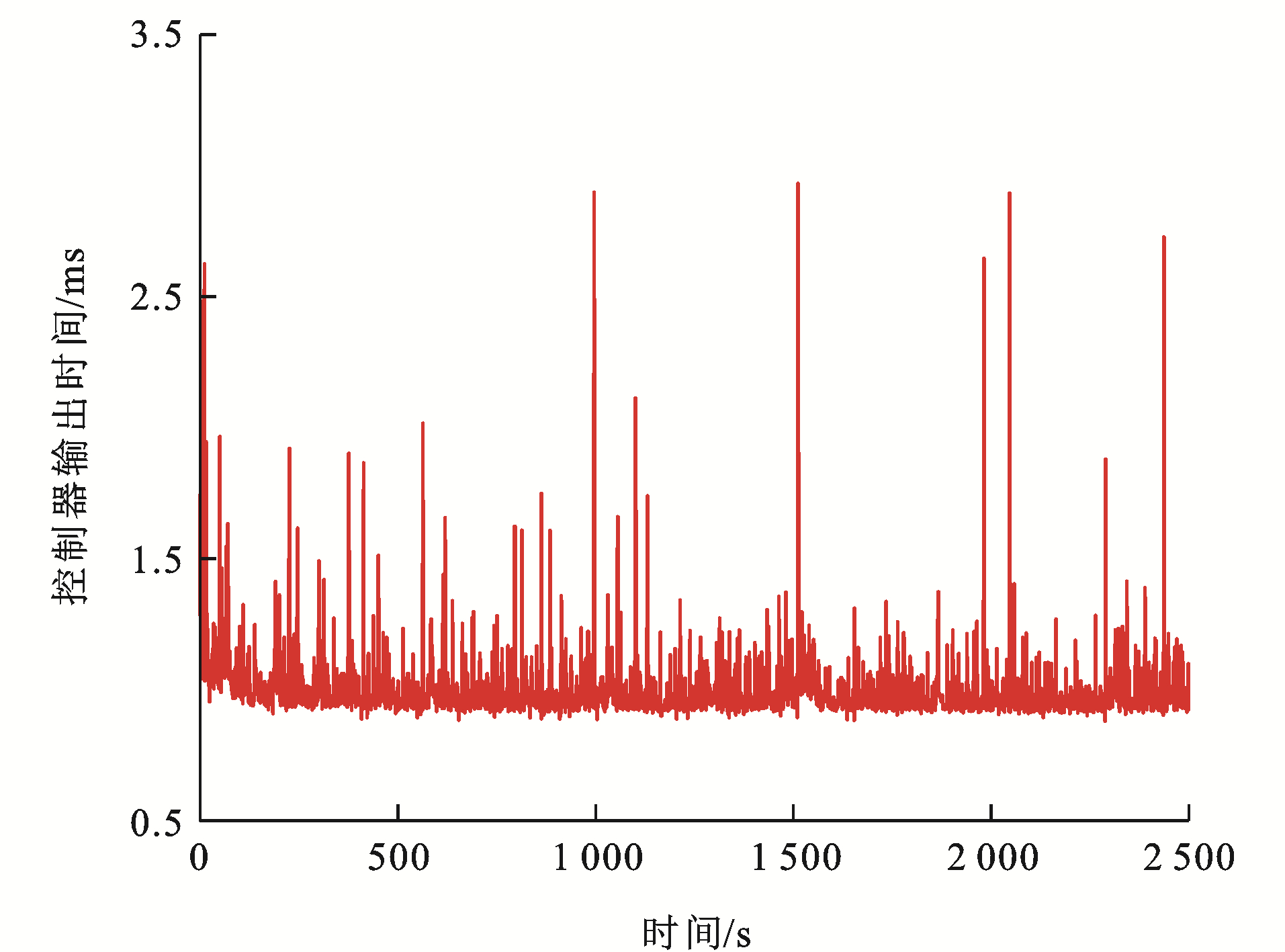
如图 23~25为各单元列车控制器在每个采样时刻的计算仿真时长，可以看出：各单元列车的单位时刻仿真时长都能保证在3 ms内，且平均仿真时长约为1 ms。根据中国列车运行控制系统三级(CTCS-3))通信系统和高速列车控制系统的要求，高速列车运行过程的采样周期需不大于10 ms，这是为了保证控制输出与实际运行过程一致。显然，IMDMPC下采样时刻的平均计算时间远小于10 ms，满足在线调节和速度跟踪控制的实时要求，验证了算法的实时性。
5. 结语
(1) 针对虚拟编组列车的协同跟踪控制问题，采用双向拓扑连接的网络通信架构构建了虚拟编组列车双向拓扑模型；通过在性能指标函数中引入邻接列车状态信息，设计了一种改进的DMPC控制算法，并从理论上证明了系统的闭环稳定性，采用4列CRH380A单元列车组成的虚拟编组列车进行了半实物仿真分析。
(2) 在不同初始条件下，列车距离误差和速度误差均能在300 s后收敛，且在收到速度调整指令后，各单元列车仍然可以保持协同稳定运行；采用IMDMPC得到的虚拟编组列车速度均方根误差和距离均方根误差分别为3.32×10-8 km·h-1和6.11×10-7 m，控制跟踪性能优于CMPC方法和DMPC方法，且各单元列车的采样时刻仿真时长均能保证在3 ms内，满足高速列车控制系统的要求，证明在IMDMPC的控制下，虚拟编组列车系统可以保证较好的稳定性、优越性和实时性控制需求。
(3) 后续研究将进一步考虑通信时延[36]和不确定干扰[37]等因素对虚拟编组列车协同运行控制造成的影响，以提升系统的控制性能，并参考已有移动闭塞下多车协同弹性间隔调整控制[38]，设计虚拟编组列车动态间隔追踪控制算法。
-
图 5 CRH380A高速列车虚拟编组模拟试验台
Figure 5. Simulation test bench for CRH380A high-speed train virtual coupling
图 17 列车0与列车1速度误差对比
Figure 17. Comparison of velocity errors between train 0 and train 1
图 18 列车0与列车1距离误差对比
Figure 18. Comparison of distance errors between train 0 and train 1
图 19 列车1与列车2速度误差对比
Figure 19. Comparison of velocity errors between train 1 and train 2
图 20 列车1与列车2距离误差对比
Figure 20. Comparison of distance errors between train 1 and train 2
图 21 列车2与列车3速度误差对比
Figure 21. Comparison of velocity errors between train 2 and train 3
图 22 列车2与列车3距离误差对比
Figure 22. Comparison of distance errors between train 2 and train 3
表 1 系统参数
Table 1. System parameters
参数 取值 单元列车质量m/t 480 单元列车车长L/m 100 基本运行阻力系数c0/(N·kg-1) 0.755 0 基本运行阻力系数c1/(N·h·kg-1·km-1) 0.006 36 基本运行阻力系数c2/(N·h2·kg-1·km-2) 0.000 115 最大加速度Umax(t)/(m·s-2) 1 最小加速度Umin(t)/(m·s-2) 1 
下载: 导出CSV
表 2 测试参数
Table 2. Test parameters
试验编号 初始速度误差/(km·h-1) 初始距离误差/m ev0, 1(0) ev1, 2(0) ev2, 3(0) es0, 1(0) es1, 2(0) es2, 3(0) 1 -5 10 -5 10 20 10 2 5 -10 10 15 25 10 3 -10 5 5 -5 10 -20 4 10 -5 -5 -10 5 10
下载: 导出CSV
表 3 列车性能调整比较
Table 3. Comparison of train performance adjustment
试验编号 性能 初始状态 稳定状态 1 各单元列车速度/(km·h-1) v0(t) 280 280 v1(t) 285 280 v2(t) 275 280 v3(t) 280 280 各单元列车间距/m es0, 1(t) 110 100 es1, 2(t) 120 100 es2, 3(t) 110 100 2 各单元列车速度/(km·h-1) v0(t) 280 280 v1(t) 275 280 v2(t) 285 280 v3(t) 275 280 各单元列车间距/m es0, 1(t) 115 100 es1, 2(t) 125 100 es2, 3(t) 110 100 3 各单元列车速度/(km·h-1) v0(t) 280 280 v1(t) 290 280 v2(t) 285 280 v3(t) 280 280 各单元列车间距/m es0, 1(t) 95 100 es1, 2(t) 110 100 es2, 3(t) 80 100 4 各单元列车速度/(km·h-1) v0(t) 280 280 v1(t) 270 280 v2(t) 275 280 v3(t) 280 280 各单元列车间距/m es0, 1(t) 90 100 es1, 2(t) 105 100 es2, 3(t) 110 100
下载: 导出CSV
表 4 算法性能指标对比
Table 4. Comparison of algorithm performance indexes
算法 Mev/(km·h-1) Mes/m W/(m2·s-4) CMPC 1.08×10-3 0.140 2 5.959 2 DMPC 8.12×10-6 2.80×10-4 3.772 5 IMDMPC 3.32×10-8 6.11×10-7 3.579 4
下载: 导出CSV
-
[1] DI MEO C, DI VAIO M, FLAMMINI F, et al. ERTMS/ETCS virtual coupling: proof of concept and numerical analysis[J]. IEEE transactions on intelligent transportation systems, 2019, 21(6): 2545-2556. [2] FLAMMINI F, MARRONE S, NARDONE R, et al. Towards railway virtual coupling[C]//IEEE. 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles and International Transportation Electrification Conference (ESARS-ITEC). New York: IEEE, 2018: 1-6. [3] 曹源, 温佳坤, 马连川. 重大疫情下的列车动态编组与调度[J]. 交通运输工程学报, 2020, 20(3): 120-128. doi: 10.19818/j.cnki.1671-1637.2020.03.011CAO Yuan, WEN Jia-kun, MA Lian-chuan. Dynamic marshalling and scheduling of trains in major epidemics[J]. Journal of Traffic and Transportation Engineering, 2020, 20(3): 120-128. (in Chinese) doi: 10.19818/j.cnki.1671-1637.2020.03.011 [4] BOCK U, BIKKER G. Design and development of a future freight train concept—"virtually coupled train formations"[J]. IFAC Proceedings Volumes, 2000, 33(9): 395-400. doi: 10.1016/S1474-6670(17)38176-4 [5] STÄNDER T, DREWES J, BRAUN I, et al. Operational and safety concepts for railway operation with virtual train-sets[J]. IFAC Proceedings Volumes, 2006, 39(12): 261-266. doi: 10.3182/20060829-3-NL-2908.00046 [6] DUAN Hua-yu, SCHMID F. Optimised headway distance moving block with capacity analysis[C]//IEEE. 2018 International Conference on Intelligent Rail Transportation (ICIRT). New York: IEEE, 2018: 1-5. [7] 刘岭. 基于虚拟耦合的列车群体智能控制技术研究及展望[J]. 铁路通信信号工程技术, 2020, 17(2): 1-9. doi: 10.3969/j.issn.1673-4440.2020.02.001LIU Ling. Research and prospect of intelligent control technology for virtually coupled train formation[J]. Railway Signalling and Communication, 2020, 17(2): 1-9. (in Chinese) doi: 10.3969/j.issn.1673-4440.2020.02.001 [8] KAVATHEKAR P, CHEN Y Q. Vehicle platooning: a brief survey and categorization[C]//ASME. Proceedings of ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Washington DC: ASME, 2011: 829-845. [9] 刘亚飞. 干扰条件下虚拟编组列车队形稳定的控制方法[D]. 北京: 北京交通大学, 2022.LIU Ya-fei. Stable platoon control for virtually coupled train set under interference conditions[D]. Beijing: Beijing Jiaotong University, 2022. (in Chinese) [10] NAUS G J L, VUGTS R P A, PLOEG J, et al. String-stable CACC design and experimental validation: a frequency-domain approach[J]. IEEE Transactions on Vehicular Technology, 2010, 59(9): 4268-4279. doi: 10.1109/TVT.2010.2076320 [11] KNORN S, DONAIRE A, AGÜERO J C, et al. Passivity-based control for multi-vehicle systems subject to string constraints[J]. Automatica, 2014, 50(12): 3224-3230. doi: 10.1016/j.automatica.2014.10.038 [12] 朱旭, 张泽华, 闫茂德. 含输入时延与通信时延的车辆队列PID控制系统稳定性[J]. 交通运输工程学报, 2022, 22(3): 184-198. doi: 10.19818/j.cnki.1671-1637.2022.03.015ZHU Xu, ZHANG Ze-hua, YAN Mao-de. Stability of PID control system for vehicle platoon with input delay and communication delay[J]. Journal of Traffic and Transportation Engineering, 2022, 22(3): 184-198. (in Chinese) doi: 10.19818/j.cnki.1671-1637.2022.03.015 [13] FELEZ J, KIM Y, BORRELLI F. A model predictive control approach for virtual coupling in railways[J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(7): 2728-2739. doi: 10.1109/TITS.2019.2914910 [14] LIU Ya-fei, ZHOU Yang, SU Shuai, et al. An analytical optimal control approach for virtually coupled high-speed trains with local and string stability[J]. Transportation Research Part C: Emerging Technologies, 2021, 125: 102886. doi: 10.1016/j.trc.2020.102886 [15] 张友兵, 刘岭. 基于虚拟编组的列车控制系统研究[J]. 铁道工程学报, 2022, 39(3): 94-100.ZHANG You-bing, LIU Ling. Research on the train control system based on virtual[J]. Journal of Railway Engineering, 2022, 39(3): 94-100. (in Chinese) [16] 宋志丹, 徐效宁, 李辉, 等. 面向虚拟编组的列控技术研究[J]. 铁道标准设计, 2019, 63(6): 155-159.SONG Zhi-dan, XU Xiao-ning, LI Hui, et al. Study on virtual-coupling-orientated train control technique[J]. Railway Standard Design, 2019, 63(6): 155-159. (in Chinese) [17] SU Shuai, LIU Wen-tao, ZHU Qing-yang, et al. A cooperative collision-avoidance control methodology for virtual coupling trains[J]. Accident Analysis and Prevention, 2022, 173: 106703. doi: 10.1016/j.aap.2022.106703 [18] SU Shuai, SHE Jiang-feng, WANG Di, et al. A stabilized virtual coupling scheme for a train set with heterogeneous braking dynamics capability[J]. Transportation Research Part C: Emerging Technologies, 2023, 146: 103947. doi: 10.1016/j.trc.2022.103947 [19] XUN Jing, LI Yan-yan, LIU Rong-hui, et al. A survey on control methods for virtual coupling in railway operation[J]. IEEE Open Journal of Intelligent Transportation Systems, 2022, 3: 838-855. doi: 10.1109/OJITS.2022.3228077 [20] WU Qing, GE Xiao-hua, HAN Qing-long, et al. Railway virtual coupling: a survey of emerging control techniques[J]. IEEE Transactions on Intelligent Vehicles, 2023, 8(5): 3239-3255. [21] WANG Xi, HU Ming-yao, WANG Hong-wei, et al. Formation control for virtual coupling trains with parametric uncertainty and unknown disturbances[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2023, 70(9): 3429-3433. [22] LIU Yu, OU Dong-xiu, YANG Yuan-xiang, et al. A method for maintaining virtually coupled states of train convoys[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 2023, 237(2): 243-252. [23] WANG Hong-wei, ZHAO Qian-qian, LIN Si-yu, et al. A reinforcement learning empowered cooperative control approach for ⅡoT-based virtually coupled train sets[J]. IEEE Transactions on Industrial Informatics, 2021, 17(7): 4935-4945. [24] XUN Jing, YIN Jia-teng, LIU Rong-hui, et al. Cooperative control of high-speed trains for headway regulation: a self-triggered model predictive control based approach[J]. Transportation Research Part C: Emerging Technologies, 2019, 102: 106-120. [25] CHEN Ming-liang, XUN Jing, LIU Ya-fei. A coordinated collision mitigation approach for virtual coupling trains by using model predictive control[C]//IEEE. 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC). New York: IEEE, 2020: 1-6. [26] SU Shai, SHE Jiang-feng, LI Kai-cheng, et al. A nonlinear safety equilibrium spacing-based model predictive control for virtually coupled train set over gradient terrains[J]. IEEE Transactions on Transportation Electrification, 2021, 8(2): 2810-2824. [27] XUN Jing, CHEN Ming-liang, LIU Ya-fei, et al. An overspeed protection mechanism for virtual coupling in railway[J]. IEEE Access, 2020, 8: 187400-187410. [28] 杨辉, 张芳, 张坤鹏, 等. 基于分布式模型的动车组预测控制方法[J]. 自动化学报, 2014, 40(9): 1912-1921.YANG Hui, ZHANG Fang, ZHANG Kun-peng, et al. Predictive control using a distributed model for electric multiple unit[J]. Acta Automatica Sinica, 2014, 40(9): 1912-1921. (in Chinese) [29] 李中奇, 金柏, 杨辉, 等. 高速动车组强耦合模型的分布式滑模控制策略[J]. 自动化学报, 2020, 46(3): 495-508.LI Zhong-qi, JIN Bai, YANG Hui, et al. Distributed sliding mode control strategy for high-speed EMUs with strong coupling model[J]. Acta Automatica Sinica, 2019, 46(3): 495-508. (in Chinese) [30] 赵凯辉, 邱鹏旗, 张昌凡, 等. 高速列车分布式速度协同跟踪控制方法研究[J]. 电子测量与仪器学报, 2022, 36(9): 12-20.ZHAO Kai-hui, QIU Peng-qi, ZHANG Chang-fan, et al. Research on distributed speed coordinated tracking control for high-speed train[J]. Journal of Electronic Measurement and Instrument, 2022, 36(9): 12-20. (in Chinese) [31] 赵超轮, 戴邵武, 赵国荣, 等. 基于分布式模型预测控制的无人机编队控制[J]. 控制与决策, 2022, 37(7): 1763-1771.ZHAO Chao-lun, DAI Shao-wu, ZHAO Guo-rong, et al. Formation control of multi-UAV based on distributed model predictive control algorithm[J]. Control and Decision, 2022, 37(7): 1763-1771. (in Chinese) [32] 陈龙, 何德峰, 李壮. 约束非线性车辆队列分布式多目标模型预测控制[J]. 控制与决策, 2022, 37(12): 3122-3128.CHEN Long, HE De-feng, LI Zhuang. Distributed multi-objective model predictive control for constrained nonlinear vehicle platoons[J]. Control and Decision, 2022, 37(12): 3122-3128. (in Chinese) [33] 戴邵武, 赵超轮, 李飞, 等. 一种多约束下无人机编队的模型预测控制算法[J]. 控制与决策, 2023, 38(3): 706-714.DAI Shao-wu, ZHAO Chao-lun, LI Fei, et al. An algorithm of model predictive control for formation control of a multi-UAV system considering multiple constraints[J]. Control and Decision, 2023, 38(3): 706-714. (in Chinese) [34] LIU Ya-fei, LIU Rong-hui, WEI Chong-feng, et al. Distributed model predictive control strategy for constrained high-speed virtually coupled train set[J]. IEEE Transactions on Vehicular Technology, 2021, 71(1): 171-183. [35] 李中奇, 周靓, 杨辉, 等. 基于预测控制的动车组迭代学习控制方法[J]. 交通运输工程学报, 2023, 23(1): 280-290. doi: 10.19818/j.cnki.1671-1637.2023.01.021LI Zhong-qi, ZHOU Liang, YANG Hui, et al. Iterative learning control method for EMUs based on predictive control[J]. Journal of Traffic and Transportation Engineering, 2023, 23(1): 280-290. (in Chinese) doi: 10.19818/j.cnki.1671-1637.2023.01.021 [36] LIU Ya-fei, ZHOU Yang, SU Shuai, et al. Control strategy for stable formation of high-speed virtually coupled trains with disturbances and delays[J]. Computer-Aided Civil and Infrastructure Engineering, 2023, 38(5): 621-639. [37] 罗啸林, 唐涛, 林炳跃, 等. 一种缩短虚拟编组列车追踪间距的鲁棒模型预测控制方法[J]. 铁道学报, 2023, 45(8): 68-76.LUO Xiao-lin, TANG Tao, LIN Bing-yue, et al. A robust model predictive control method to shorten the tracking distance of virtual marshalling trains[J]. Journal of the China Railway Society, 2023, 45(8): 68-76. (in Chinese) [38] SHANGGUAN Wei, LUO Rui, SONG Hong-yu, et al. High-speed train platoon dynamic interval optimization based on resilience adjustment strategy[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 23(5): 4402-4414. -
下载:
点击查看大图
计量
- 文章访问数: 347
- HTML全文浏览量: 105
- PDF下载量: 27
- 被引次数: 0
