0.   引言

航海模拟器作为经济、高效的仿真平台, 对培训船舶驾驶人员起着重要作用, 而航海模拟器的行为真实感^[1]主要取决于船舶运动数学模型的精准性与可靠性。当前中国航海模拟器所采用的船舶运动数学模型大部分依赖进口软件生成, 为提高中国航海模拟器的国产化水平及自主可控性, 同时满足国际海事组织(International Maritime Organization, IMO)对船舶操纵性能的要求^[2], 建立高精度、适用性强的波浪中船舶运动数学模型对航海模拟器具有重要的工程意义。

任俊生等^[3]采用经验公式计算了船舶水动力系数, 并建立了高速水翼双体船在规则波浪中的垂荡纵摇运动模型; 张秀凤等^[4]基于傅汝德-克雷洛夫(Froude-Krylov, F-K)力假设, 初步为航海模拟器建立了规则波浪中船舶六自由度运动数学模型; 钱小斌等^[5]基于F-K力假设, 建立了波浪中船舶1、2阶波浪力数值计算模型, 但是文献[3]~[5]都对复杂的船舶几何形状进行了简化处理, 较大地限制了船舶运动模型的数值预报精度及船型适用范围。

由于计算机性能的飞速提高, 基于三维时域理论对波浪中船舶水动力及运动建模已经成为当前的重要研究方向, 相对于二维理论^[6]及三维频域理论^[7]来说, 三维时域理论在解决船舶的瞬态、非线性及操纵问题上具有较强优势, 可有效满足航海模拟器对船舶运动数学模型的要求。在势流理论范畴内, Liapis等^{[8, 9]}基于瞬时自由面格林函数^{[10, 11]}建立了静水中有航速船舶的三维时域线性水动力分析模型, 并在船体平均湿表面上计算其辐射力; King等^{[12, 13, 14, 15]}进一步利用脉冲响应函数法研究了三维时域线性绕射问题, 避免了在不同频率入射波浪下重新求解扰动速度势边界积分方程。由于瞬时自由面格林函数在近自由液面处具有强烈振荡增幅特性, 扰动势边界积分方程中的水线项不能有效提高水动力系数的数值精度。在船舶大幅度摇荡时, 船体湿表面积发生较大变化, 此时线性理论已不能完全准确地数值预报波浪中船舶的水动力及运动。

Lin等^[16]基于物面非线性理论, 采用瞬时自由面格林函数法建立了扰动速度势在自由液面下的瞬时船体湿表面积分方程。由于扰动势速度求解需要在每个时间步长调用瞬时自由面格林函数, 并求解数目庞大的矩阵方程, 耗时巨大, 严重降低了航海模拟器的实时性。由于F-K力及静恢复力非线性对船舶运动有显著影响^[17], F-K力与静恢复力在船舶瞬时湿表面上精确、高效的计算成为预报波浪中船舶运动的有效方法^[18]。Singh等^{[19, 20]}采用干-湿网格判断法生成船舶瞬时湿表面网格, 细分整个船体(包括水线面以上船体部分), 其中计算F-K力与静恢复力所需细网格的面元面积为计算扰动力所需粗网格面元面积的1/4~1/8, 船舶瞬时湿表面生成方法效率较高, 但是当面元尺寸比面元中心点与入射波面之间的相对距离大时, 相邻2个时间步长内面元与波面的相交情况可能发生突变, F-K力的数值计算极易发生波动; Sengupta等^[21]采用瞬时网格截取法划分船舶瞬时湿表面网格, 其计算F-K力与静恢复力的面元尺度与计算扰动力粗网格的面元尺度一样, 所生成的船舶瞬时湿表面网格与波面吻合良好, 由于在求解面元与瞬时波面的交点坐标时采用了迭代法, 每一时间步都需要更新面元位置信息, 计算较为繁琐, 且当入射波波幅和波长比较大时, 面元与波面的相交情况不易判断; Rodrigues等^{[22, 23]}对整个船体表面进行了网格划分, 其中瞬时湿表面面元尺度仍与计算流体扰动力粗网格的面元尺度一样, 采用四叉树划分法对与波面相交面元进一步细分, 并合并每层相邻子面元, 其子面元合并处理比较复杂, 并未有效修正波面条件, 且船体表面所受F-K力与静压力的合压力在未扰动自由液面处发生跳跃。采用频时域转换法计算扰动力时, 高频区域水动力系数数值计算容易产生较大误差, 造成船舶运动预报精度的下降。

为建立高精度、适用性强的船舶运动数学模型, 本文基于三维F-K力非线性法建立规则波浪中船舶运动的数学模型; 为计入F-K力和静恢复力的非线性, 研究一种基于四叉树划分对船体瞬时湿表面进行动态网格生成的方法, 并进一步修正静压力与入射波压力; 在三维线性时域理论范畴内采用瞬时自由面格林函数法求出船体所受的扰动力, 并分析水线项对船舶水动力的影响; 对Wigley Ⅰ型船^[24]进行数值计算, 将数值计算结果与试验数据及其他文献结果进行充分比对, 以验证本文建立的规则波浪中船舶运动数学模型的可靠性与精准性。

1.   数学模型

1.1   流域与坐标系定义

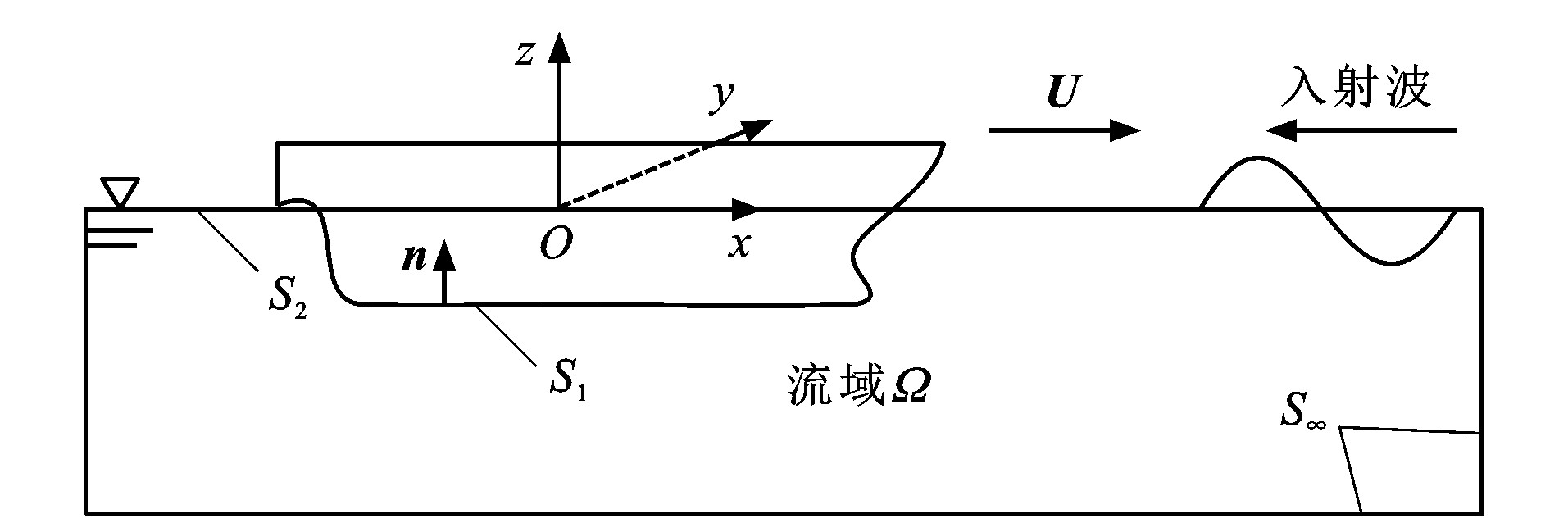
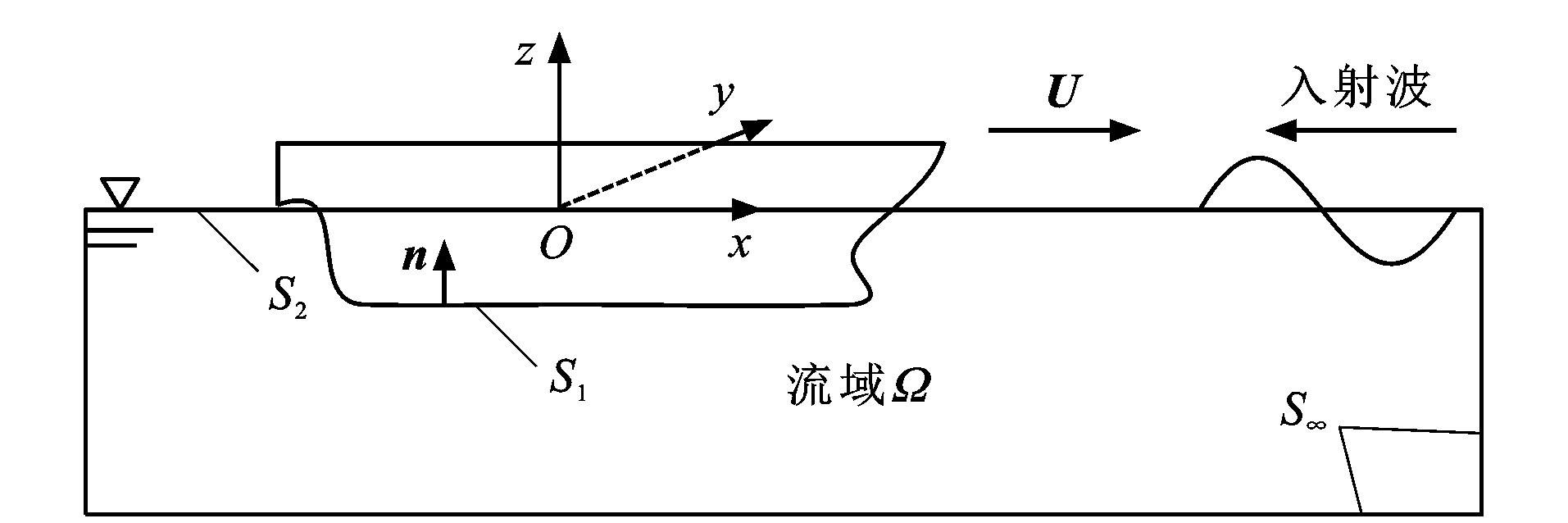
流域和坐标系定义见图 1, 采用参考坐标系Oxyz研究波浪中以定常航速U前进的船舶, 定常航速U与x轴(指向船首)平行; 参考坐标系Oxyz随船舶以定常航速U一起运动; 原点O位于船中, xOz面与未扰动自由液面(z=0, z为垂向)重合, y轴指向左舷; 流域Ω的表面由船体平均湿表面S₁、线性自由液面S₂及无穷远处控制面S_∞组成; 单位法线矢量n指向船体内部。

图  1  流域和坐标系定义

Figure  1.  Definitions of fluid domain and coordinate system

下载: 全尺寸图片 幻灯片

1.2   扰动速度势满足的初边值条件

势流理论范畴内, 假定流体不可压缩、无黏性及流动无旋。在参考坐标系Oxyz下流场总速度势Φ₁基于线性理论^[12]可以分解为

$\begin{array}{l}\Phi {}_1=-Ux+\Phi {}_2(x,y,z)+\text{ϕ}{}_0(x,y,z,t)+\\ {\displaystyle \sum _{k=1}^7\text{ϕ}}{}_k(x,y,z,t)(1)\end{array}$

式中: t为当前时刻; Φ₂(x, y, z)为定常兴波速度势; ϕ₀(x, y, z, t)为入射波速度势; ϕ_k(x, y, z, t)为不定常速度势, 其中ϕ₁(x, y, z, t)、ϕ₂(x, y, z, t)、…、ϕ₆(x, y, z, t)为辐射速度势, ϕ₇(x, y, z, t)为绕射速度势。

不定常速度势ϕ_k(x, y, z, t)需要满足流域Ω内的Laplace方程以及S₁、S₂和S_∞的边界条件与初始条件^[12]。可采用瞬时自由面格林函数G(x₁, y₁, z₁, x₂, y₂, z₂, t, τ)求解上述初边值定解问题^{[11, 25, 26, 27]}, 其中: (x₁, y₁, z₁)和(x₂, y₂, z₂)分别为场点P和源点Q的坐标; τ为过去某一时刻。不定常速度势ϕ_k(x₁, y₁, z₁, t)所满足的边界积分方程为^[12]

式中: t₀为初始时刻; G₀(x₁, y₁, z₁, x₂, y₂, z₂)和G₁(x₁, y₁, z₁, x₂, y₂, z₂, t, τ)分别为G(x₁, y₁, z₁, x₂, y₂, z₂, t, τ)的瞬时部分和波动部分; S为船体表面积分面积变量; γ为S₁与S₂的交线, 即船舶水线; n_Q为源点Q处单位法线矢量; g为重力加速度。

1.3   辐射问题与绕射问题求解

结合式(2), 基于脉冲响应函数法, 由k(k=1, 2, …, 6)模态运动所引起的j(j=1, 2, …, 6)模态辐射力F_jk(t)可以表示为^[26]

$\begin{array}{l}F{}_{jk}(t)=-a{}_{jk}\stackrel{\cdot \cdot }{{\displaystyle \zeta }}{}_k(t)-b{}_{jk}\stackrel{\cdot }{{\displaystyle \zeta }}{}_k(t)-c{}_{jk}\zeta {}_k(t)-\\ {\displaystyle {\int }_0^t\text{d}}\tau \kappa {}_{jk}(t-\tau )\stackrel{\cdot }{{\displaystyle \zeta }}{}_k(\tau )(3)\end{array}$

式中: a_jk为k模态运动引起的j模态下与船体几何形状有关的系数; b_jk、c_jk均为k模态运动引起的j模态下与航速和船体几何形状相关的系数; κ_jk(t)为k模态运动引起的j模态下与船体几何形状、时间及航速相关的系数; ζ_k(t)为船舶运动的k模态分量。

三维频域内的附加质量A_jk(ω)(ω为波浪圆频率)与阻尼系数B_jk(ω)可由傅里叶变换^[28]得到, 则在参考坐标系Oxyz下, 入射波波面升高η(t)为

$\begin{array}{l}\eta (t)=\eta {}_0\text{e}{}^{\text{i}\omega {}_{\text{e}}t}(4)\\ \omega {}_{\text{e}}=\omega -U{\rm K}\cos (\alpha )(5)\end{array}$

式中: η₀为入射波波幅; ω_e为遭遇频率; α为浪向角, 迎浪方向为π; K为波数。

则场点P的入射波速度势ϕ₀(x₁, y₁, z₁, t)可以表示为

$\text{ϕ}{}_0(x{}_1,y{}_1,z{}_1,t)=\frac{\text{i}\eta {}_{0}g}{\omega }\text{e}{}^{{\rm K}\{z{}_1-\text{i}[x{}_1\cos (\alpha )+y{}_1\sin (\alpha )]\}}\text{e}{}^{\text{i}\omega {}_{\text{e}}t}(6)$

入射波波面升高η(t)可以作为线性时域系统的输入, 令W(x₁, y₁, z₁, t)为入射波速度势所产生的速度场的脉冲响应函数, 则入射波速度势的速度场∇ϕ₀(x₁, y₁, z₁, t)^[8]可表示为

∇ϕ₀(x₁, y₁, z₁, t)=∫ ${}_{-\infty }^{+\infty }$ dτW(x₁, y₁, z₁, t-τ)η(τ) (7)

基于脉冲响应函数法及傅里叶变换, 结合式(2)、(6)和(7)可求得绕射势ϕ₇(x₁, y₁, z₁, t)的脉冲响应函数φ(x₁, y₁, z₁, t)^[13]。则j模态绕射力F_j7(t)的脉冲响应函数W_j7(t)为

$\begin{array}{l}W{}_{j7}(t)=\rho {\displaystyle \underset{S{}_1}{\iint }\text{ϕ}}{}_7(x{}_1,y{}_1,z{}_1,t)m{}_j\text{d}S-\\ \rho {\displaystyle \underset{S{}_1}{\iint }\frac{\partial \text{ϕ}{}_7(x{}_1,y{}_1,z{}_1,t)}{\partial t}}n{}_j\text{d}S(8)\end{array}$

式中: ρ为流体密度; n_j(j=1, 2, …, 6)为广义法线向量的j模态分量; m_j为恒定速度产生的j模态梯度。

则j模态绕射力F_j7(t)为

$F{}_{j7}(t)={\displaystyle \int }{}_{-\infty }^{+\infty }\eta (\tau )W{}_{j7}(t-\tau )\text{d}\tau (9)$

1.4   F-K力与静恢复力求解

参考坐标系Oxyz下场点P(x₁, y₁, z₁)(z₁≤0)处的静压力p_H(x₁, y₁, z₁, t)与入射波压力p_I(x₁, y₁, z₁, t)分别为

$\begin{array}{l}p{}_{\text{Η}}(x{}_1,y{}_1,z{}_1,t)=-\rho gz{}_1(10)\\ p{}_{\text{Ι}}(x{}_1,y{}_1,z{}_1,t)=\rho g\eta {}_0\text{e}{}^{{\rm K}z{}_1}\cos [\omega {}_{\text{e}}t-\\ {\rm K}x{}_1\cos (\alpha )-{\rm K}y{}_1\sin (\alpha )](11)\end{array}$

则场点P的入射波压力p_I(x₁, y₁, z₁, t)与静压力p_H(x₁, y₁, z₁, t)的合压力p(x₁, y₁, z₁, t)为

$p(x{}_1,y{}_1,z{}_1,t)=\rho g\eta (t)\text{e}{}^{{\rm K}z{}_1}-\rho gz{}_1(12)$

为满足入射波面上的压力为0且沿吃水方向压力连续分布, 需要进一步修正式(12)^[29]。当η(t)≥0时, 场点P的合压力p(x₁, y₁, z₁, t)为

$p(x{}_1,y{}_1,z{}_1,t)=\{\begin{array}{cc}\rho g\eta (t)-\rho gz{}_1\hfill & 0\le z{}_1\le \eta (t)\hfill \\ \rho g\eta (t)\text{e}{}^{{\rm K}z{}_1}-\rho gz{}_1\hfill & z{}_1<0\hfill \end{array}(13)$

当η(t) < 0时, 为满足总压力在波面上为0的条件, 需要修正波谷, 求解非线性方程η(t)e^₁Kz-ρgz₁=0时采用迭代法, 波谷经过修正后可得z₁=η(t)e^₁Kz, 则场点P的合压力p(x₁, y₁, z₁, t)为

$p(x{}_1,y{}_1,z{}_1,t)=\{\begin{array}{cc}0\hfill & \eta (t)\text{e}{}^{{\rm K}z{}_1}\le z{}_1\le 0\hfill \\ \rho g\eta (t)\text{e}{}^{{\rm K}z{}_1}-\rho gz{}_1\hfill & z{}_1<\eta (t)\text{e}{}^{{\rm K}z{}_1}\hfill \end{array}(14)$

j模态F-K力F_jI(t)及静恢复力F_jH(t)分别为

$\begin{array}{l}F{}_{j\text{Ι}}(t)={\displaystyle \underset{S(t)}{\iint }p}{}_{\text{Ι}}(x{}_1,y{}_1,z{}_1,t)n{}_j\text{d}S(15)\\ F{}_{j\text{Η}}(t)={\displaystyle \underset{S(t)}{\iint }p}{}_{\text{Η}}(x{}_1,y{}_1,z{}_1,t)n{}_j\text{d}S(16)\end{array}$

式中: S(t)为t时刻船体瞬时湿表面。

1.5   运动微分方程求解

将F_jk(t)、F_jI(t)、F_j7(t)及F_jH(t)代入船舶运动方程, 则规则波浪中船舶运动方程可以写为^[26]

$\begin{array}{l}{\displaystyle \sum _{k=1}^6}[({\rm M}{}_{jk}+a{}_{jk})\stackrel{\cdot \cdot }{{\displaystyle \zeta }}{}_k(t)+b{}_{jk}\stackrel{\cdot }{{\displaystyle \zeta }}{}_k(t)+c{}_{jk}\zeta {}_k(t)+\\ {\displaystyle {\int }_0^t\text{d}}\tau \kappa {}_{jk}(t-\tau )\stackrel{\cdot }{{\displaystyle \zeta }}{}_k(\tau )]=F{}_{j\text{Ι}}(t)+\\ F{}_{j\text{Η}}(t)+F{}_{j7}(t)(17)\end{array}$

式中: M_jk为广义质量矩阵的元素。

式(17)可采用四阶Runge-Kutta法求解, 并在初始短时间内对式(17)右端作用力应用平滑函数^[14], 以避免初始扰动造成运动时间历程的数值发散。

2.   数值实现

2.1   不定常速度势边界积分方程数值求解

采用常数面元法求解式(2), 其步骤为: 将船体平均湿表面S₁划分为一定数目的粗网格面元; 将船舶水线γ划分为一定数目的线元; 每块面元上的不定常速度势和每段线元上的扰动速度势均为常值, 并与相邻面元上的扰动速度势相等; G₀(x₁, y₁, z₁, x₂, y₂, z₂)在平面四边形上的面元积分可采用Hess-Smith法^[25]计算, G₁(x₁, y₁, z₁, x₂, y₂, z₂, t, τ)在平面四边形上的面元上积分采用高斯积分求得; 在对时间进行积分时, 时间步长Δt设为定值, 并采用向前欧拉方法进行积分; 对式(2)中的卷积积分部分采用梯形法则进行数值计算。为减小由瞬时自由面格林函数剧烈振荡增幅引起的水动力计算数值误差, 舍去了船舶水线γ的积分项。

2.2   船舶瞬时湿表面上的F-K力数值积分

首先将船体全部划分(包括水线面以上部分)为一定数量的粗网格面元。图 2为船体表面面元划分种类示意。根据其与波面的相对位置可将船体表面划分为湿面元、干面元与部分湿面元3种。

图  2  面元与瞬时波面的相对位置

Figure  2.  Relative positions between panel and instantaneous wave profile

下载: 全尺寸图片 幻灯片

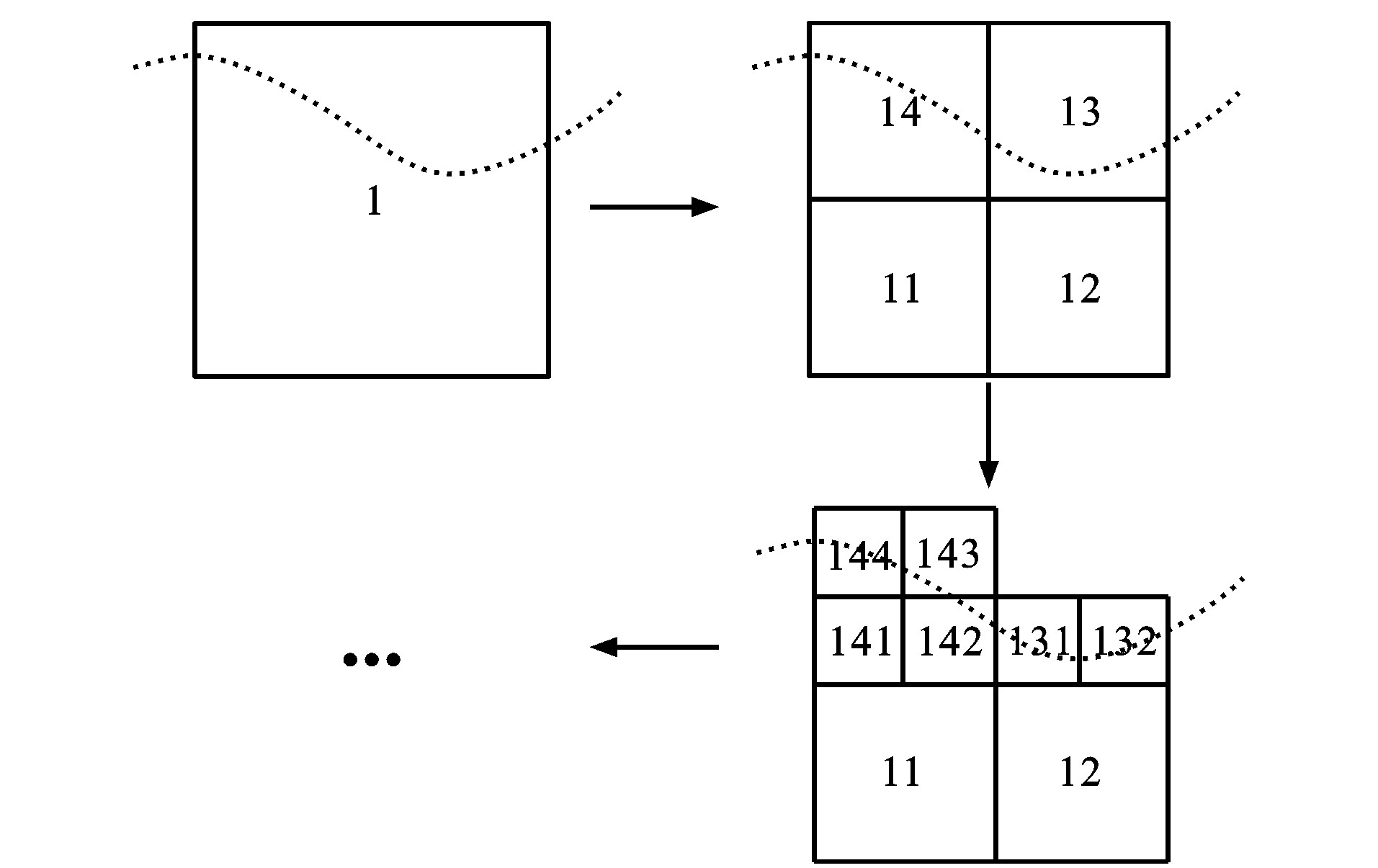
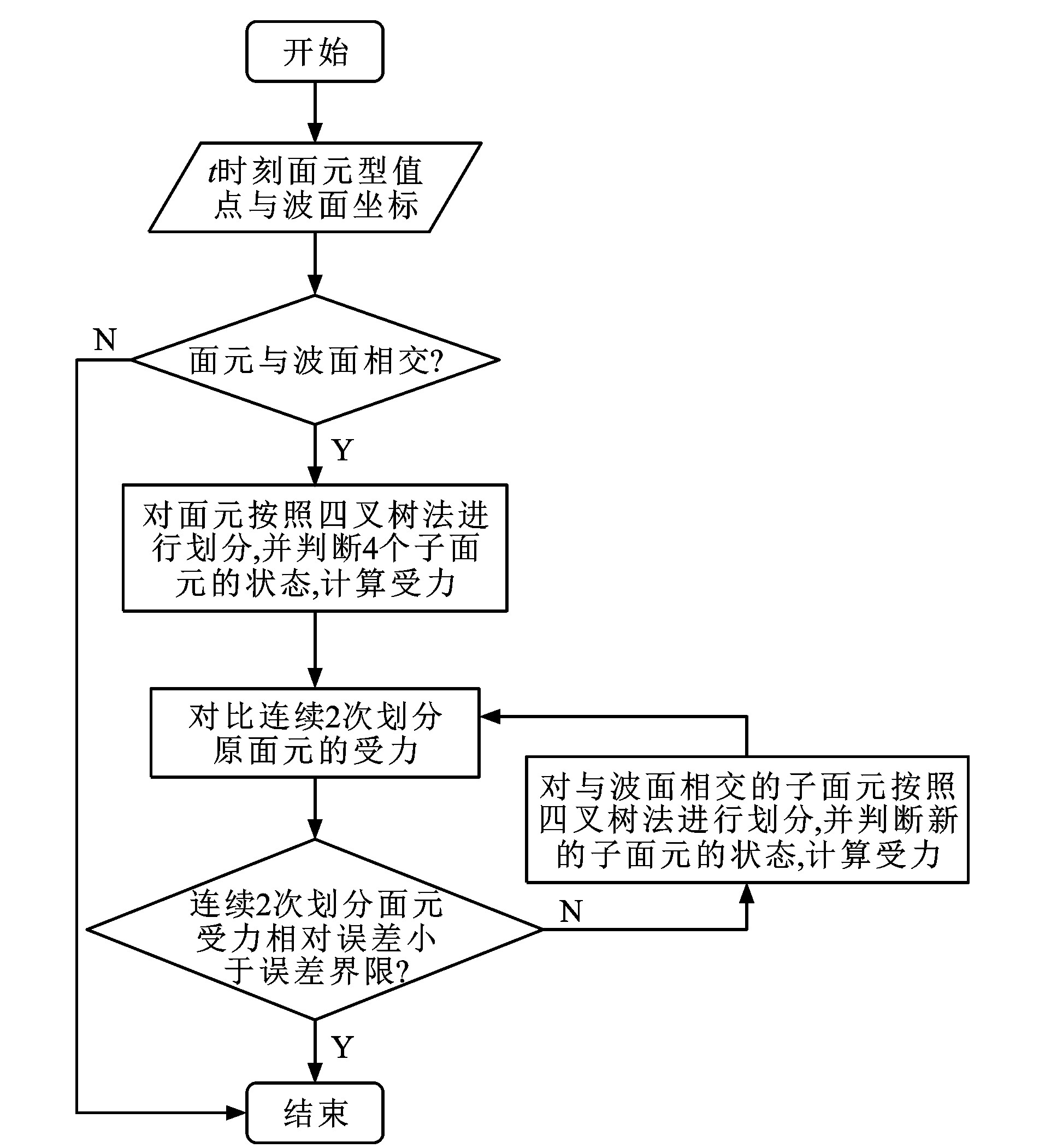
图 3为与波面相交部分湿面元的四叉树划分示意。对于湿面元, 面元上受到的F-K力可由入射波压力进行2×2高斯积分数值求解得到; 对于干面元, 入射波产生的F-K力为0;对于部分湿面元, 由于F-K力的变化比其他面元大(图 3), 采用高斯积分并结合四叉树划分法对F-K力进行高精度数值计算; 对于新生成的子面元, 如果子面元中心位于瞬时入射波下, 其F-K力计算与湿面元相同, 反之则与干面元相同。图 4为部分湿面元受力计算流程, 根据实际工程需要可对图 4中的误差界限进行调整, 本文采用的误差界限为10^-5 N。

图  3  面元的四叉树划分

Figure  3.  Panel subdivision by quad-tree

下载: 全尺寸图片 幻灯片

图  4  面元受力计算流程

Figure  4.  Calculation process of forces acting on panel

下载: 全尺寸图片 幻灯片

3.   数值模拟结果分析

3.1   计算仿真对象

考虑到船舶运营经济性, 一般远洋航行的船舶傅汝德数小于0.3。由于Wigley Ⅰ型船舶在傅汝德数为0.2时, 纵摇运动出现共振现象, 本文取傅汝德数0.2来验证所建立的规则波浪中船舶运动模型的可靠性。波浪参数设定为浪向角α=π。Wigley Ⅰ型船舶面元划分如图 5所示, 其主要参数如表 1所示。

图  5  Wigley Ⅰ型船舶面元分布

Figure  5.  Panel distribution of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

表  1  Wigley Ⅰ型船舶参数

Table  1.  Parameters of Wigley Ⅰ hull

参数	船长L/m	船宽/m	吃水/m	排水体积/m3	纵摇惯性半径	重心与基线距离/m	方形系数
数值	3	0.3	0.187 5	0.094 6	0.25L	0.17	0.56

下载: 导出CSV 

| 显示表格

3.2   辐射问题分析及验证

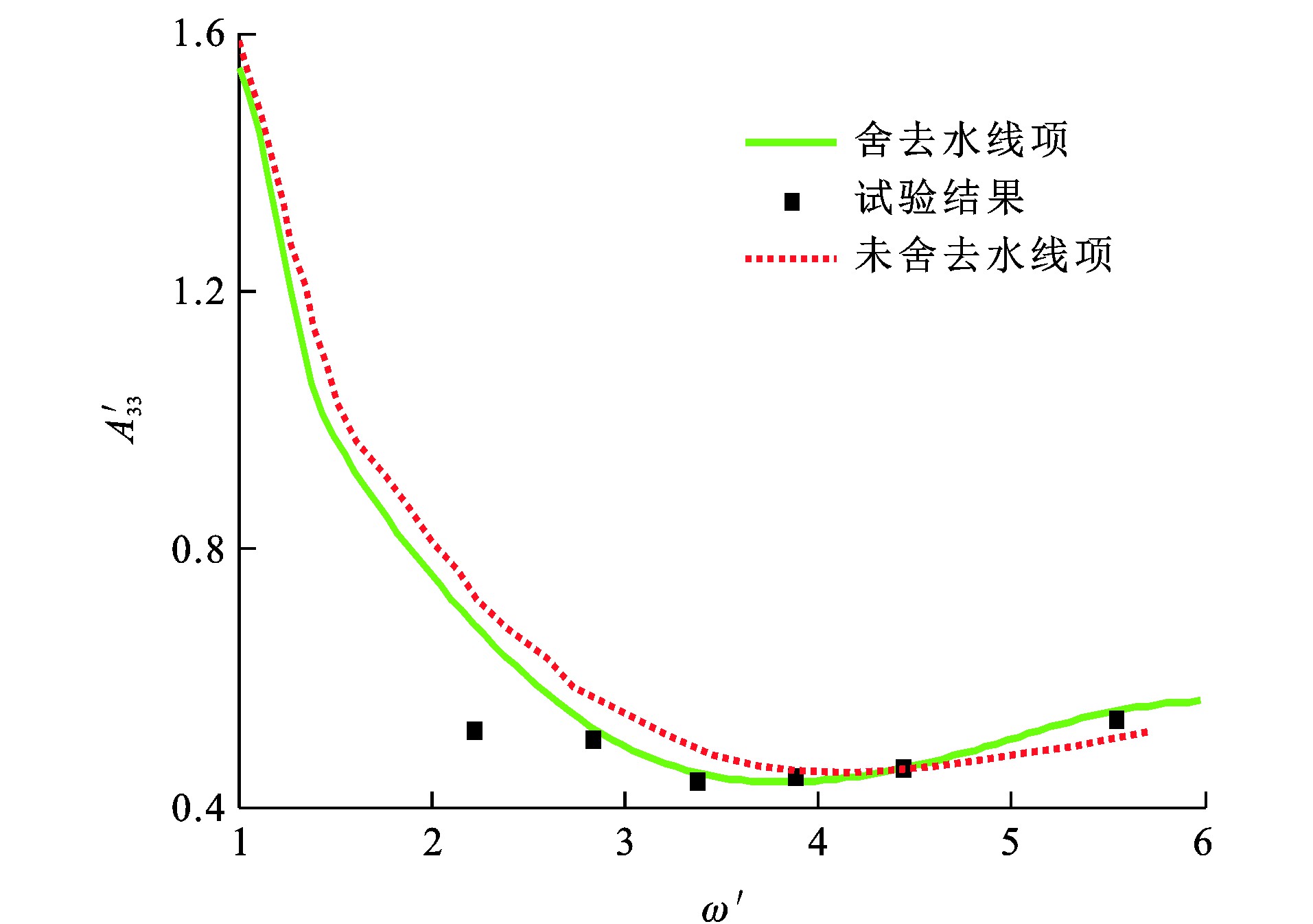
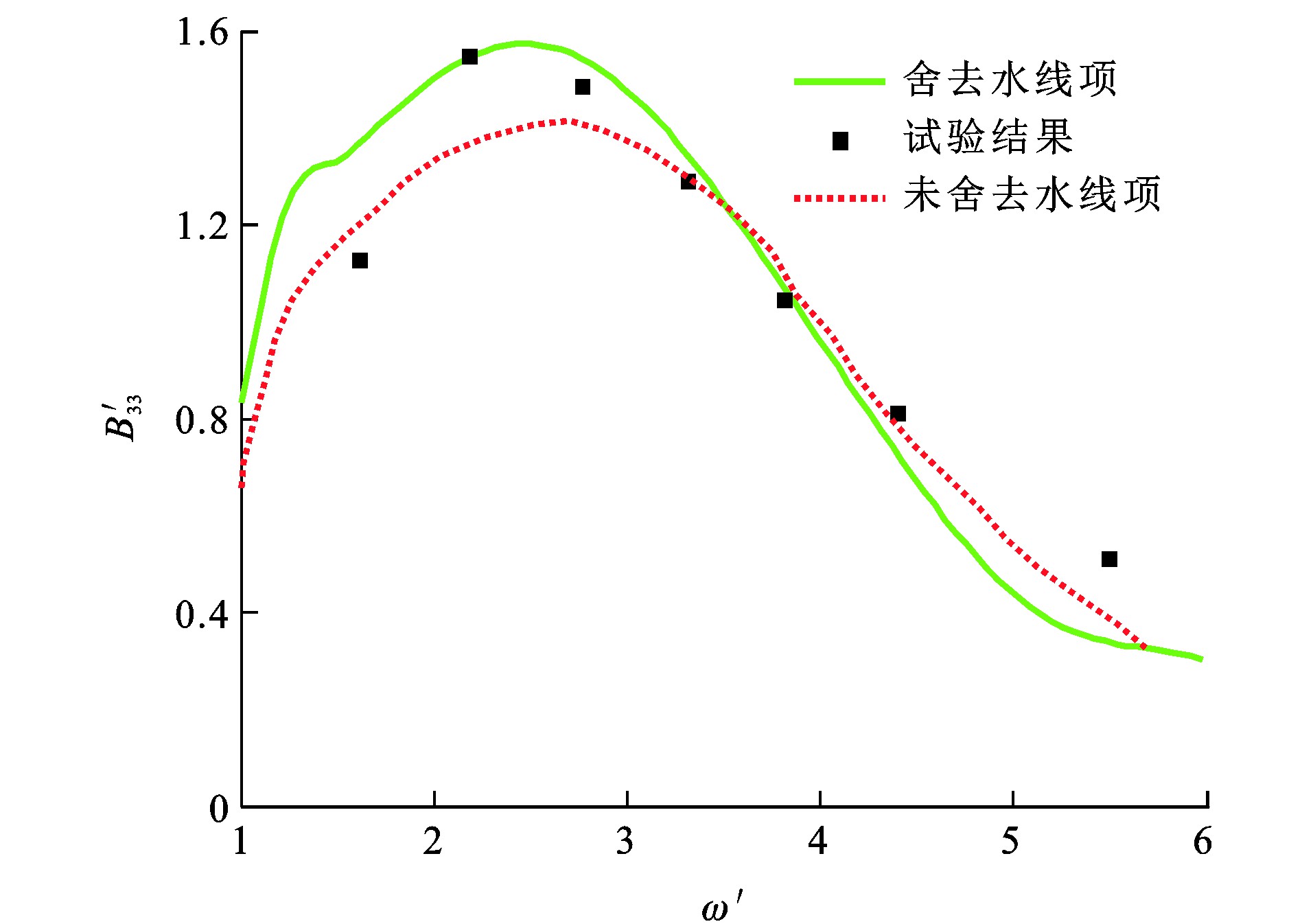
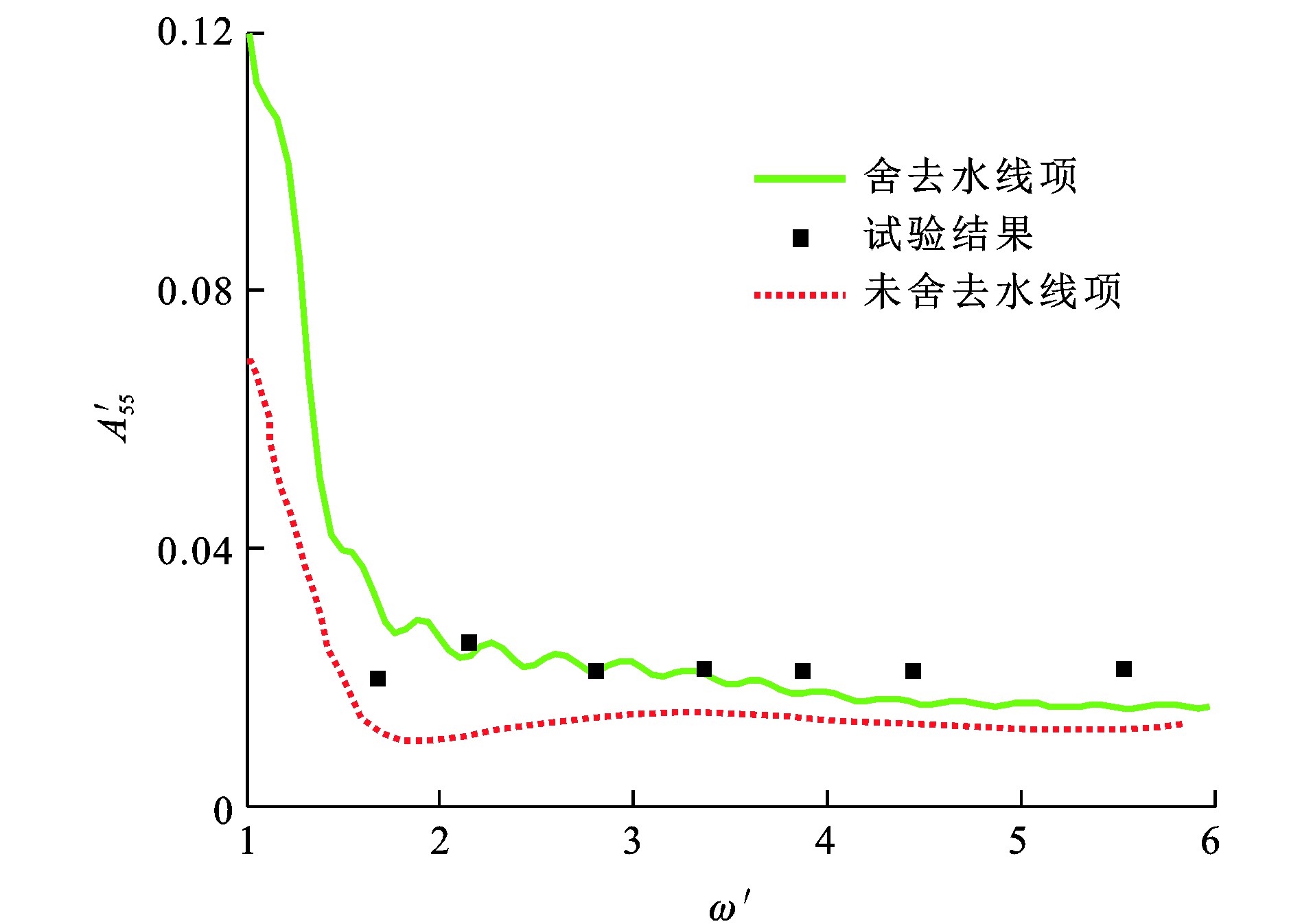
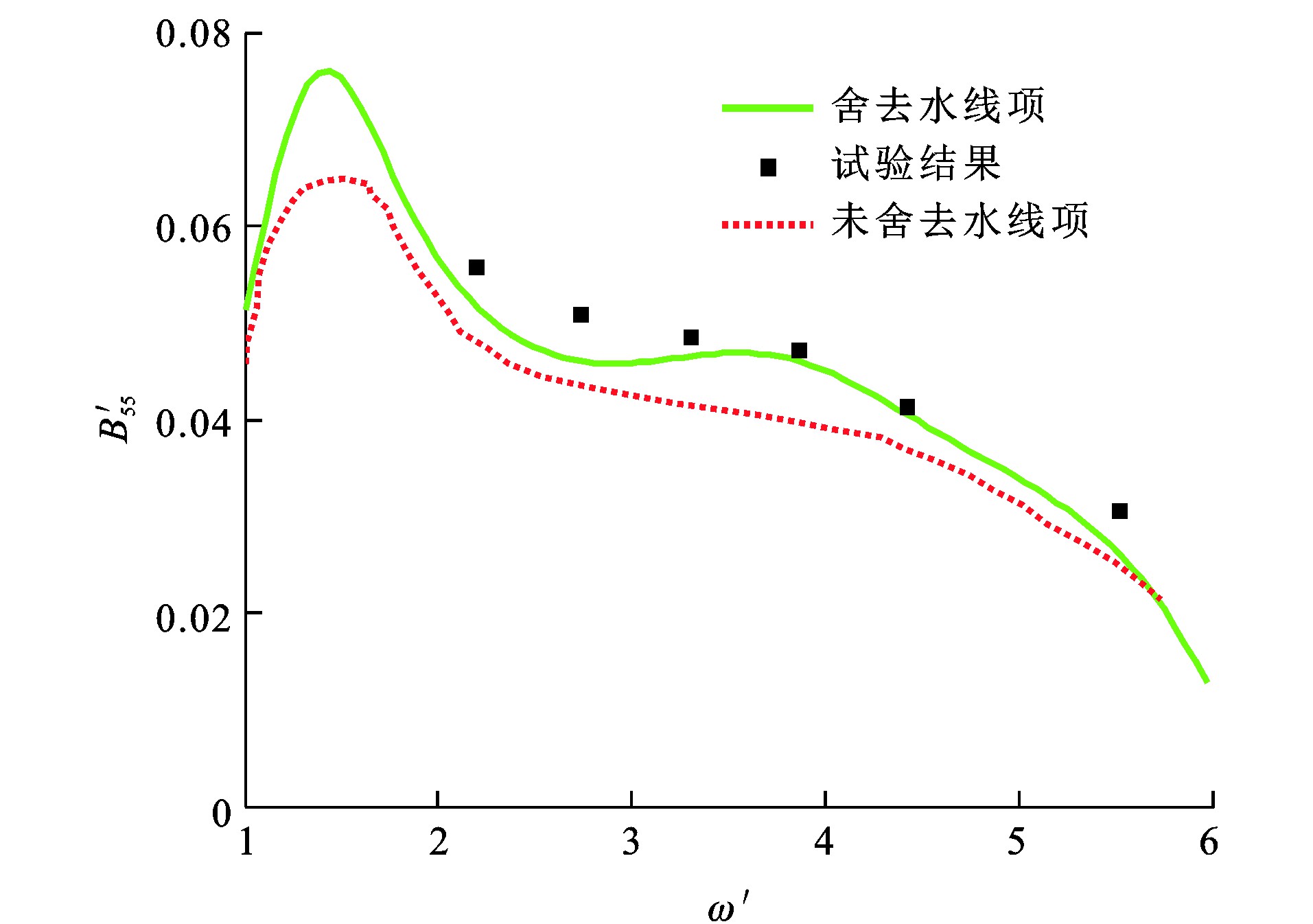
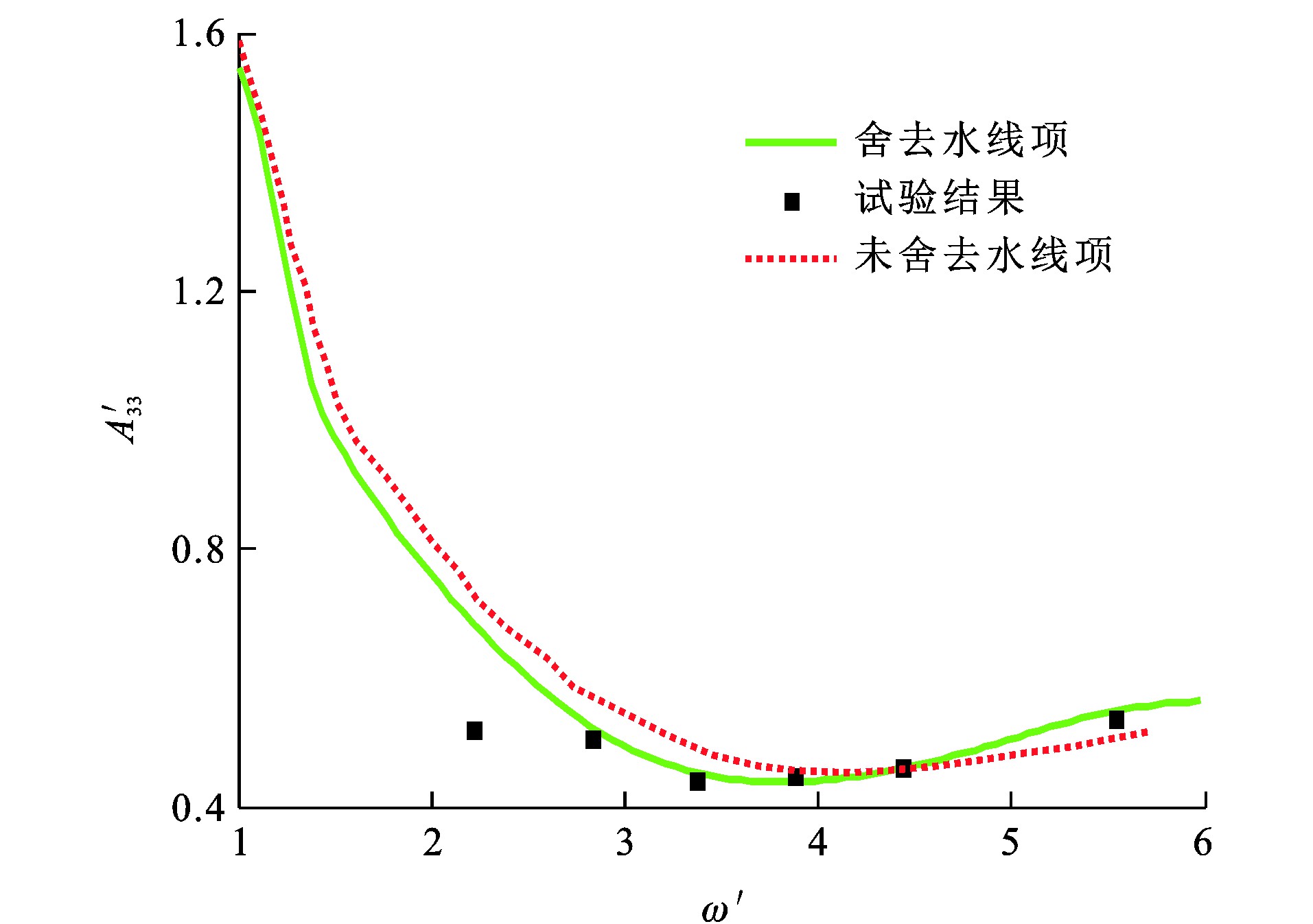
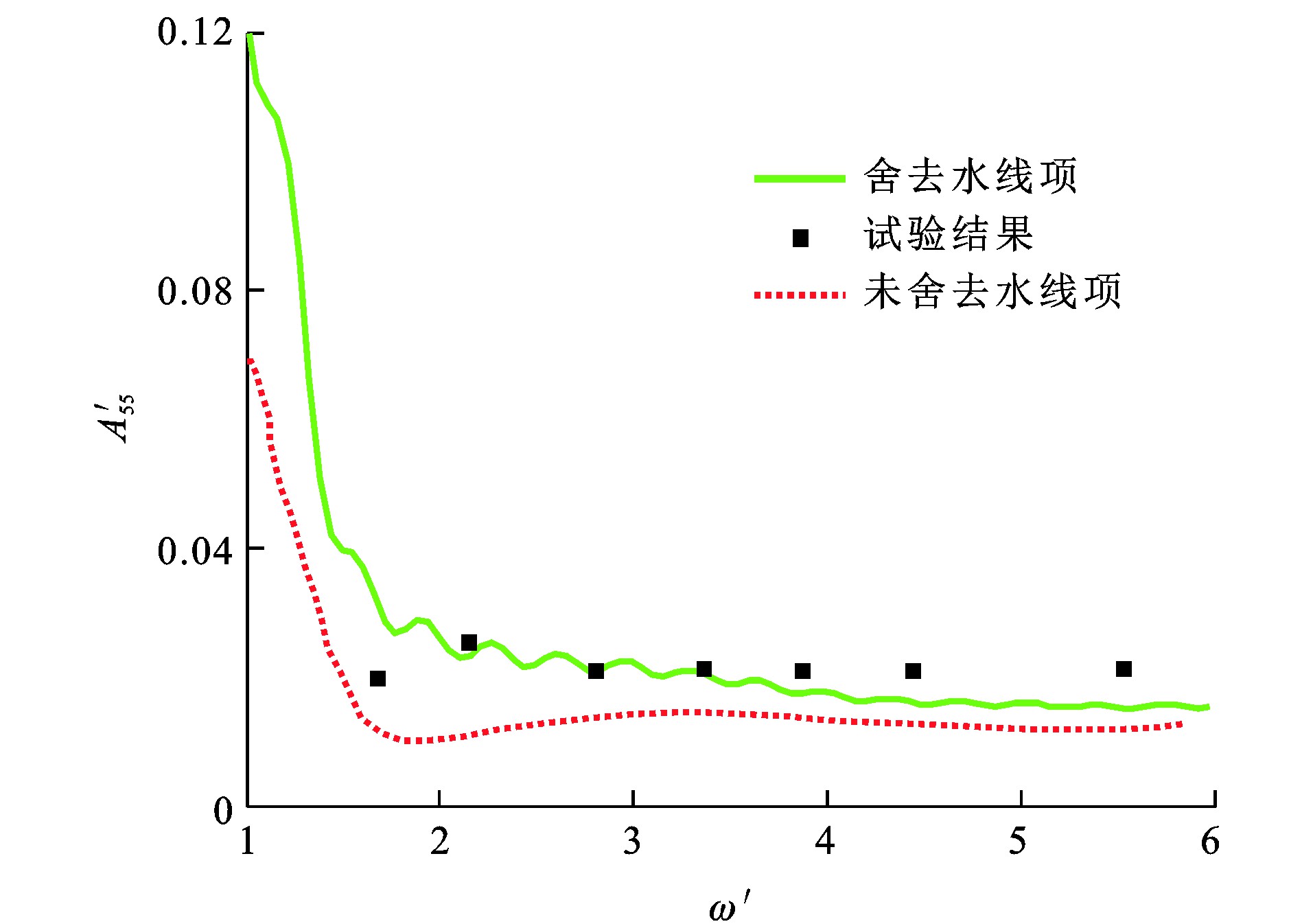
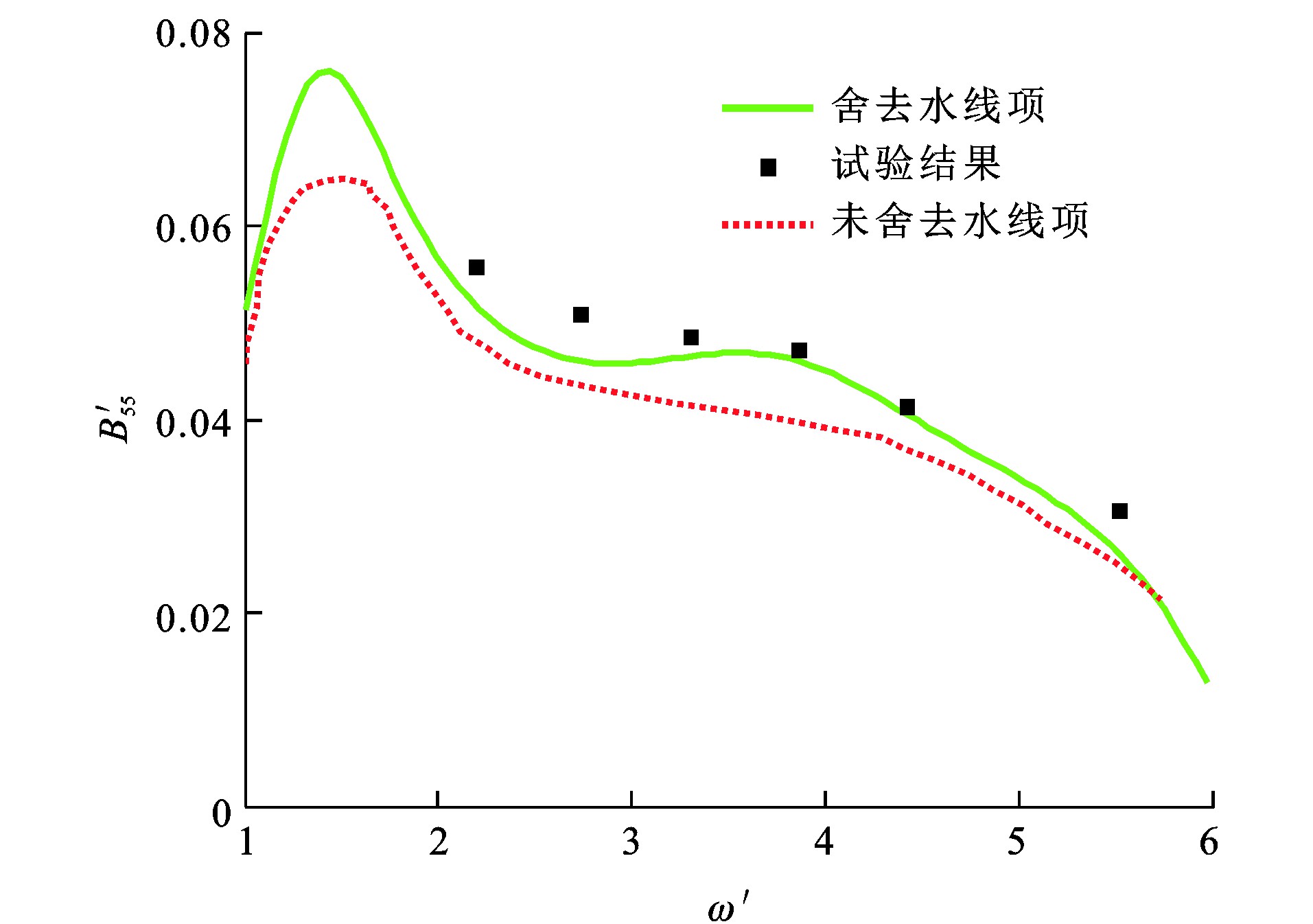
为研究船舶水线项对其扰动力的影响, 对影响船舶水动力性能较大的水动力系数(附加质量和阻尼系数)A₃₃、A₅₅和B₃₃、B₅₅进行充分比对。A₃₃、A₅₅、B₃₃、B₅₅和ω的量纲一形式分别为A′₃₃、A′₅₅、B′₃₃、B′₅₅及ω′^[26]。图 6~9为Wigley Ⅰ型船舶量纲一水动力系数, 本文方法舍去水线项, 而Magee等^[30]采用的方法未舍去水线项, 可知: 由于临界频率的影响^[26], ω′≈1.7处水动力系数与试验结果^[24]有较大偏差, 舍去水线项计算所得量纲一垂荡附加质量比试验值低44.0%;在其他频率处, 舍去水线项计算所得水动力系数与试验值的最大相对误差最大为33.4%, 未舍去水线项计算所得水动力系数与试验值的最大相对误差为54.8%;在大部分频率范围内, 舍去水线项的数值计算结果比未舍去水线项时更接近试验结果。原因在于, 瞬时自由面格林函数在自由液面处具有剧烈的振荡增幅特性, 计算水线项积分时容易造成较大数值误差, 而实际上流体具有一定的黏性, 瞬时自由面格林函数在自由液面不可能无限地振荡增幅, 且船体几何形状一般是细长的, 舍去水线项可以改善水动力系数的预报性能。

图  6  Wigley Ⅰ型船舶量纲一垂荡附加质量

Figure  6.  Non-dimensional heave added masses of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

图  7  Wigley Ⅰ型船舶量纲一垂荡阻尼系数

Figure  7.  Non-dimensional heave damping coefficients of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

图  8  Wigley Ⅰ型船舶量纲一纵摇附加质量

Figure  8.  Non-dimensional pitch added masses of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

图  9  Wigley Ⅰ型船舶量纲一纵摇阻尼系数

Figure  9.  Non-dimensional pitch damping coefficients of Wigley Ⅰ hull

下载: 全尺寸图片 幻灯片

3.3   面元所受F-K力数值计算与船体瞬时湿表面生成

本文在计算F-K力时, 将整个船体剖分成80×8个粗网格面元, 并对与瞬时波面相交的粗网格面元进行四叉树划分(图 3), 称为方案1;Singh等^[19]对粗网格面元进一步细分, 将整个船体划分为160×16个面元, 称为方案2;对方案1中的粗网格面元不断划分, 直到作用在面元上的作用力在指定误差10^-5 N内, 作为方案1、2的参考, 称之为方案3。

波浪参数设定: 波长λ船长比λ/L为1.5, 入射波波幅η₀为0.054 m。在t=0时刻, 选取A、B、C与D这4块与瞬时波面相交的面元, 其中心在参考坐标系Oxyz中的坐标分别为(-1.462 5, -0.008 4, -0.023 4)、(-1.387 5, -0.024 4, -0.023 4)、(-1.312 5, -0.039 1, -0.023 4)和(-0.112 5, -0.149 2, 0.070 3)。由方案3可得作用在A、B、C及D上的F-K力分别为-0.397 44、-0.389 72、-0.333 55及0.235 59 N。表 2为采用方案1计算的面元上的F-K力, 可知: 当面元划分次数不小于4时, 入射波在面元上的压力积分不再发生变化, 此时方案1与方案3的计算结果都在误差精度10^-5 N内。当划分次数为1时, 对粗网格只进行一次划分, 相当于方案2的处理效果, 此时面元上的F-K力较方案3存在较大误差, 甚至达到100%。

表  2  采用方案1对F-K压力在面元上的积分结果

Table  2.  F-K pressures integration results on panels by scheme 1  N

面元划分次数	面元A	面元B	面元C	面元D
1	-0.433 70	-0.332 26	-0.239 42	0.000 00
2	-0.422 23	-0.351 28	-0.336 21	0.490 38
3	-0.397 04	-0.382 73	-0.328 53	0.235 59
4	-0.397 44	-0.389 72	-0.333 55	0.235 59
5	-0.397 44	-0.389 72	-0.333 55	0.235 59

下载: 导出CSV 

| 显示表格

由于波面F-K力较大且波动较为剧烈, 仅对部分湿面元进行一次划分是不够的, 因此, 本文提出的方案1能更好地计算部分湿面元上的F-K力。表 3为采用3种方案计算的面元上的F-K力。在t=0时, 选取a、b、c与d这4块完全位于波面下的面元, 其面元中心在参考坐标系Oxyz中的坐标分别为(0.937 0, -0.026 9, -0.164 1)、(0.937 5, -0.066 3, -0.117 2)、(0.937 5, -0.086 3, -0.070 3)和(0.937 5, -0.096 0, -0.023 4)。方案1中采用粗网格面元, 由于面元位于波面下, 入射波波动性较弱, 不需要进一步划分。方案2对粗网格面元进行一次划分, 将1个粗网格面元细分为4个细网格面元, 并采用高斯积分计算F-K力。

表  3  采用不同方案对F-K压力在面元上积分的结果

Table  3.  F-K pressures integration results on panels adopting different schemes  N

方案编号	a	b	c	d
1	0.599 12	0.479 36	0.471 82	0.483 95
2	0.599 12	0.479 36	0.471 82	0.483 95
3	0.599 12	0.479 36	0.471 82	0.483 95

下载: 导出CSV 

| 显示表格

表 3为方案1、2及3对面元a、b、c及d上F-K压力积分结果。以面元a为例, 采用方案1、2、3进行面元F-K力数值计算的时间分别为0.000 332、0.001 079和0.014 522 s, 其计算结果见表 3, 可知: 方案1、2、3的数值计算结果相同, 但方案1的耗时是方案2的1/3, 有效地提高了计算效率。

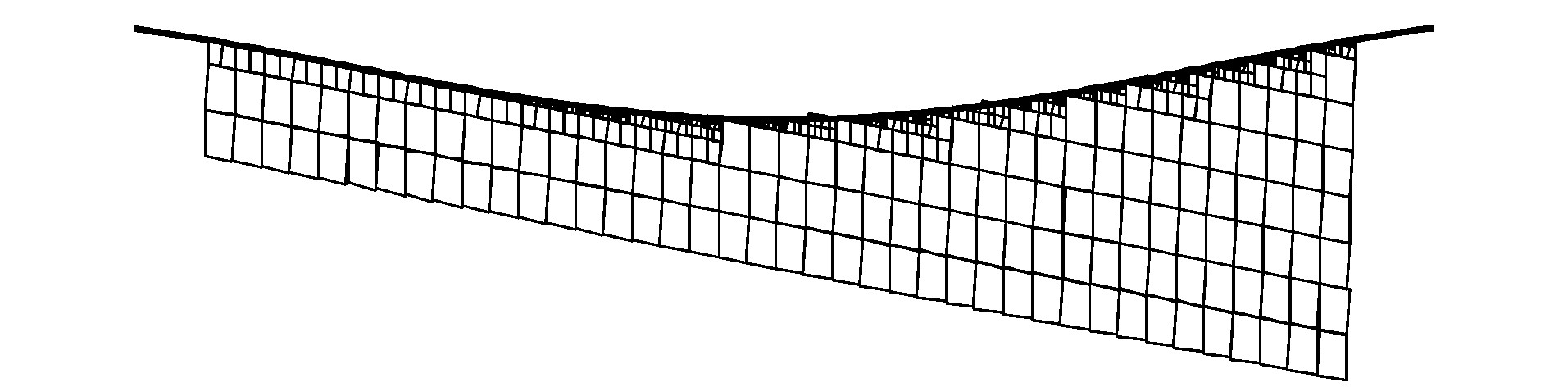
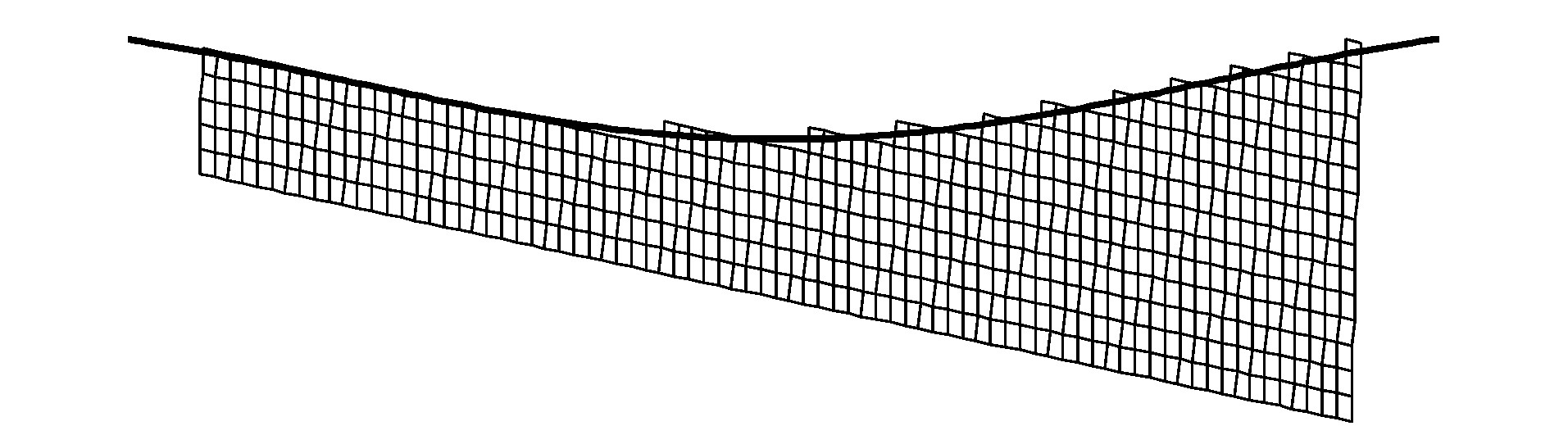
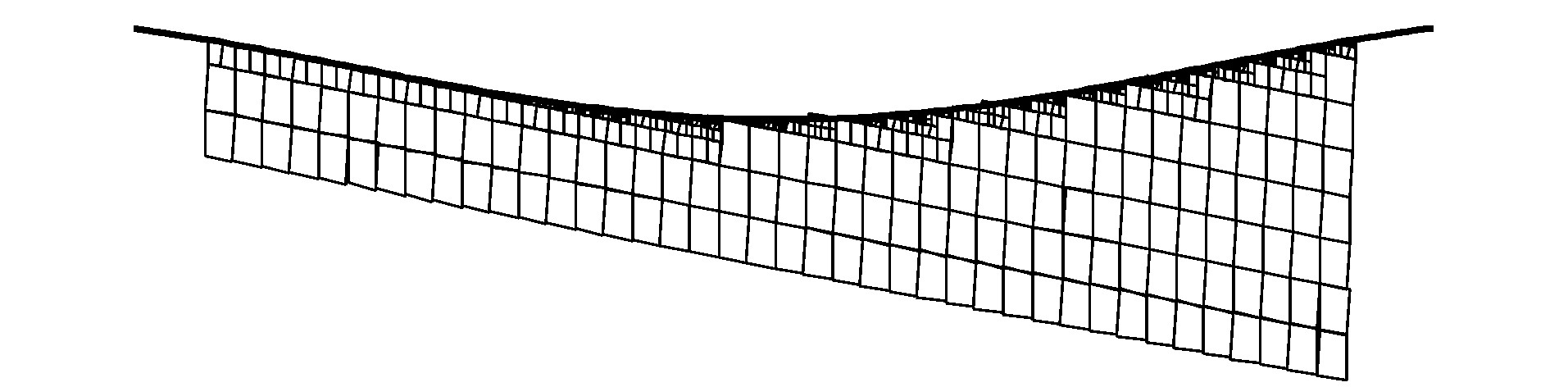
图 10、11为t=1.81 s时瞬时入射波波面下船舶湿表面网格划分示意, 可知: 采用方案2生成的船舶瞬时湿表面在入射波波面上的面积部分更为明显, 表明方案1生成的船舶瞬时湿表面与入射波波面吻合更好。

图  10  采用方案1时瞬时入射波波面下的船体面元划分

Figure  10.  Panel division of hull under instantaneous incident wave profile when using scheme 1

下载: 全尺寸图片 幻灯片

图  11  采用方案2时瞬时入射波波面下的船体面元划分

Figure  11.  Panel division of hull under instantaneous incident wave profile when using scheme 2

下载: 全尺寸图片 幻灯片

3.4   F-K力时历与船舶运动仿真

为将本文方法与Journée^[24]的试验结果及其他文献计算结果对比, 数值仿真Wigley Ⅰ型船舶垂荡与纵摇2个自由度的F-K力及运动状态。

3.4.1   F-K力与运动时历

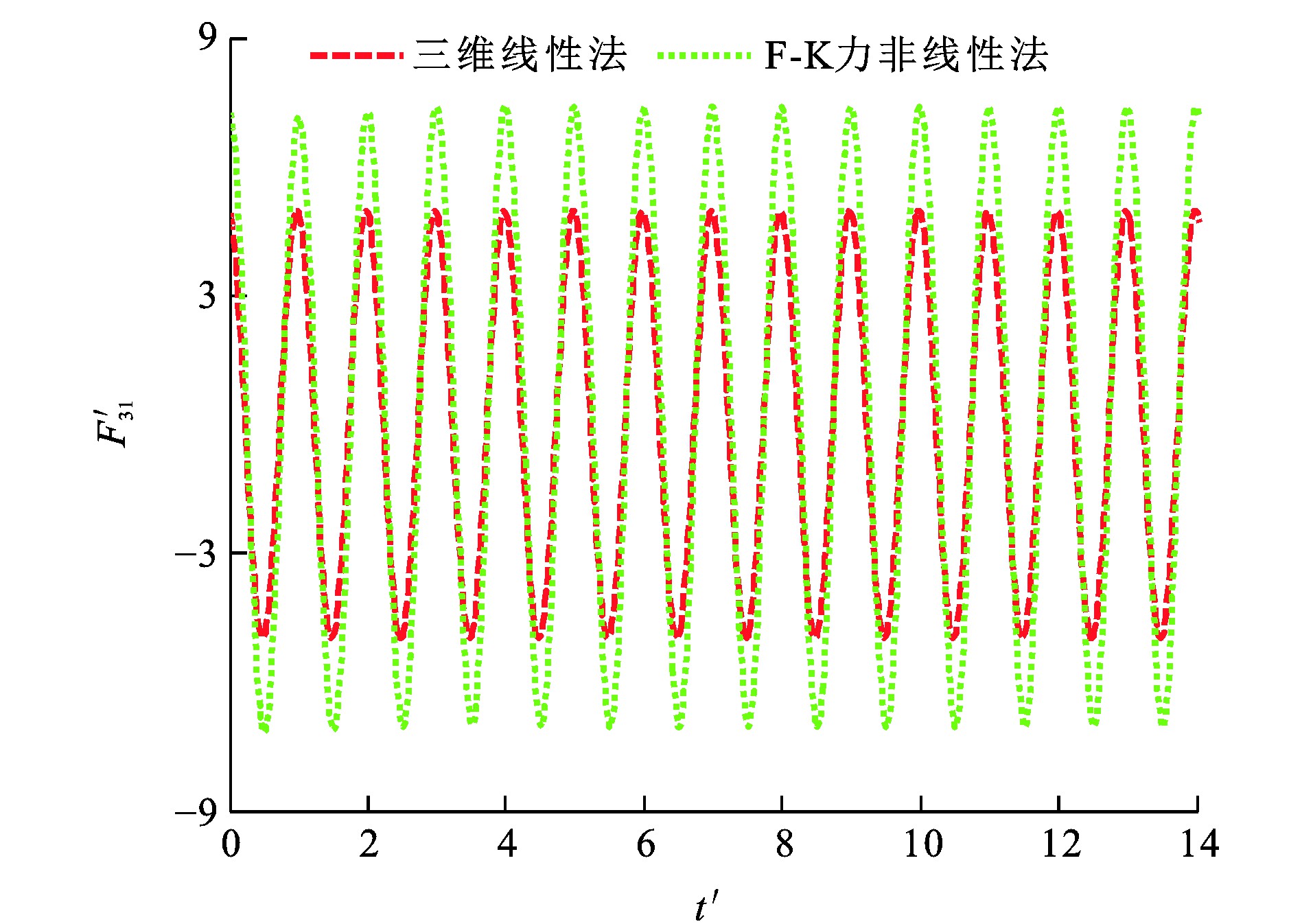
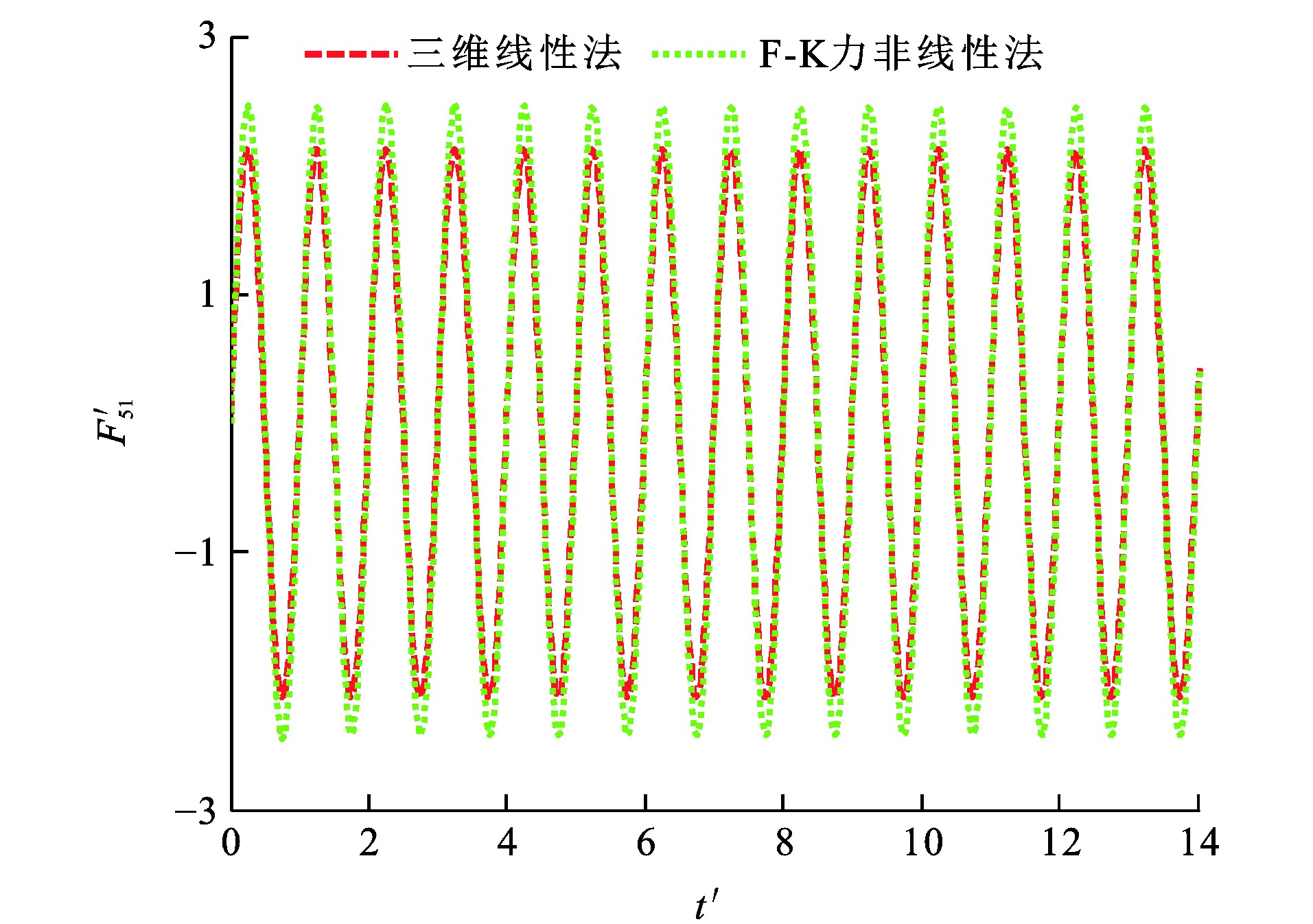
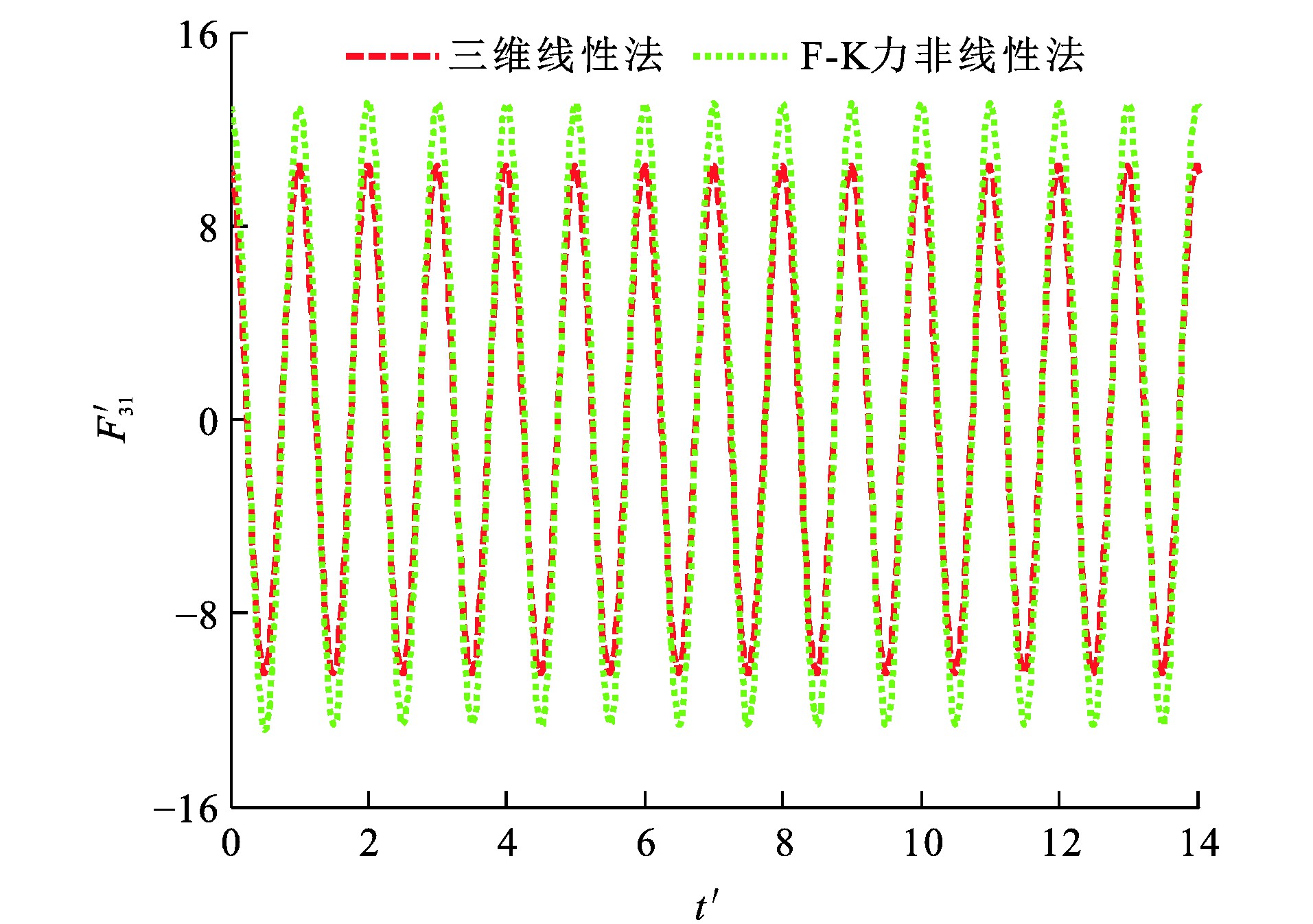
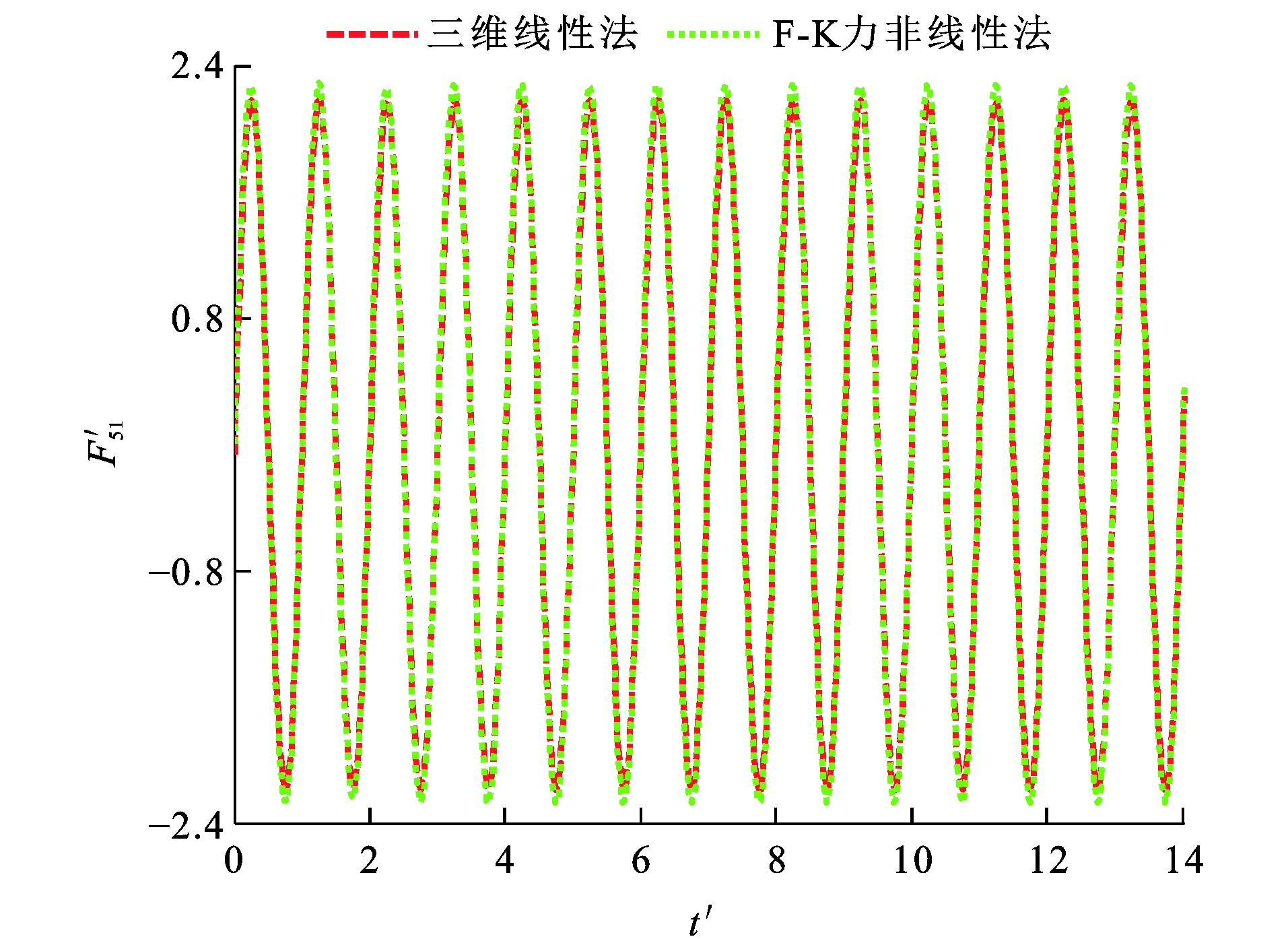
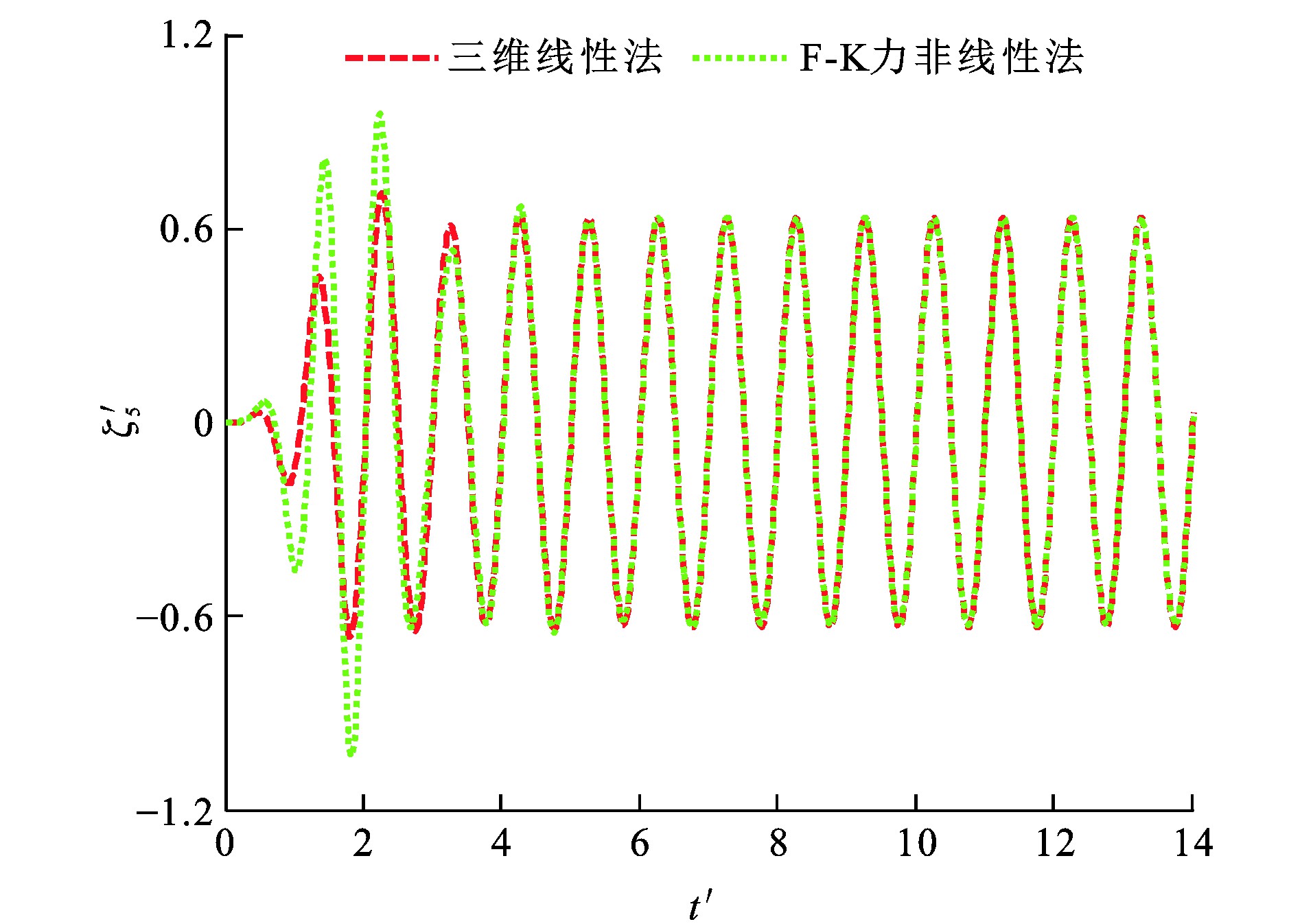
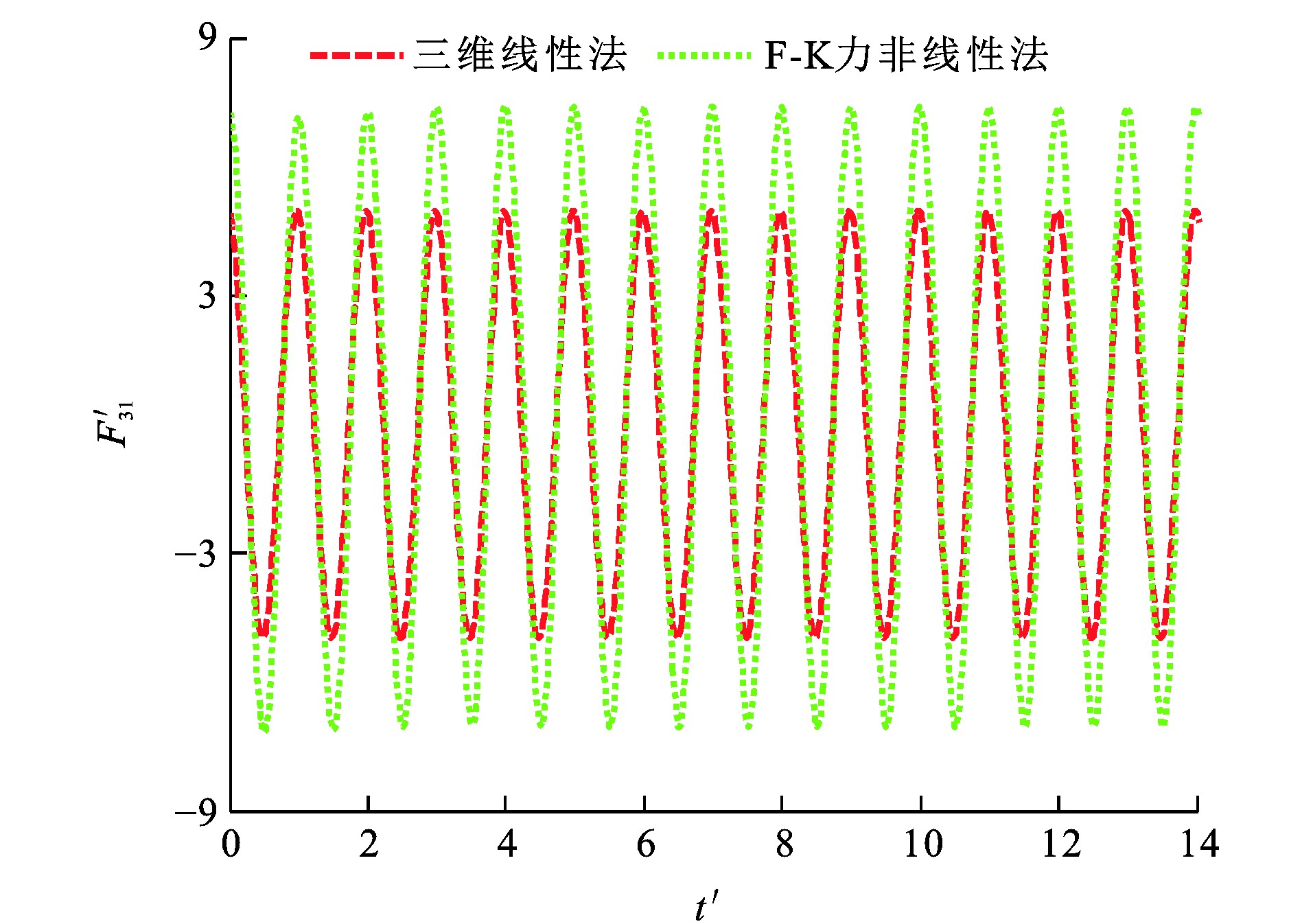
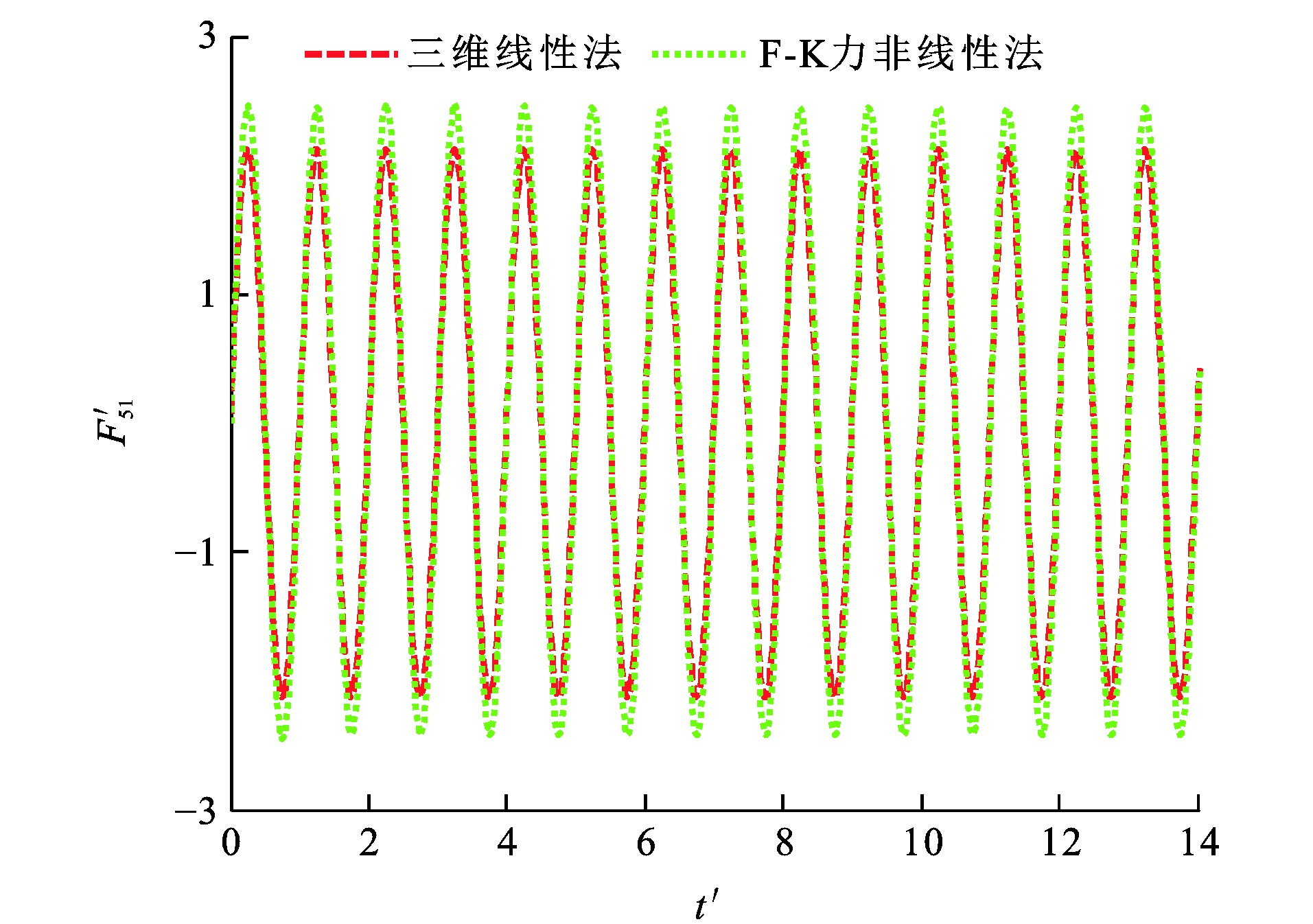
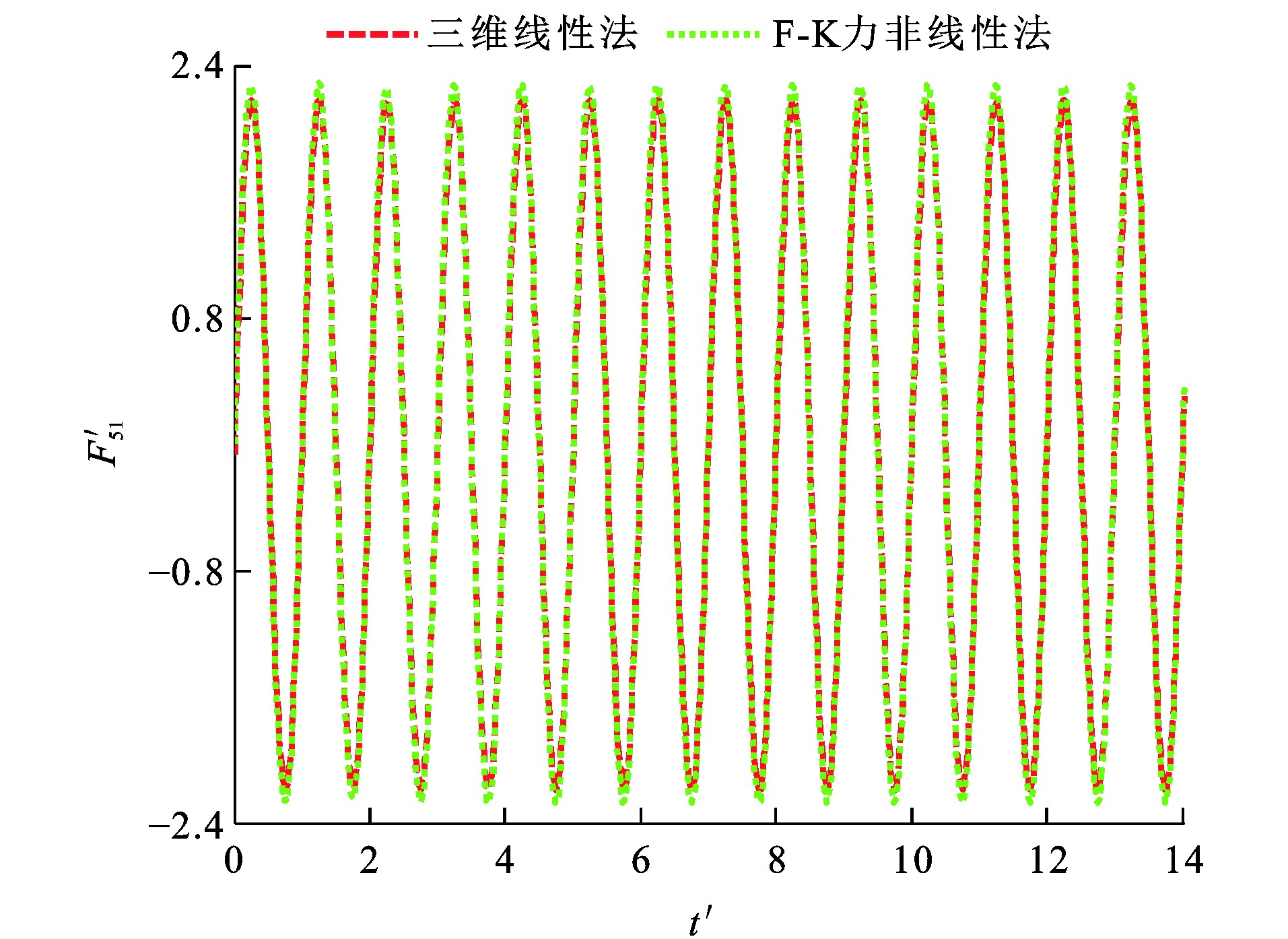
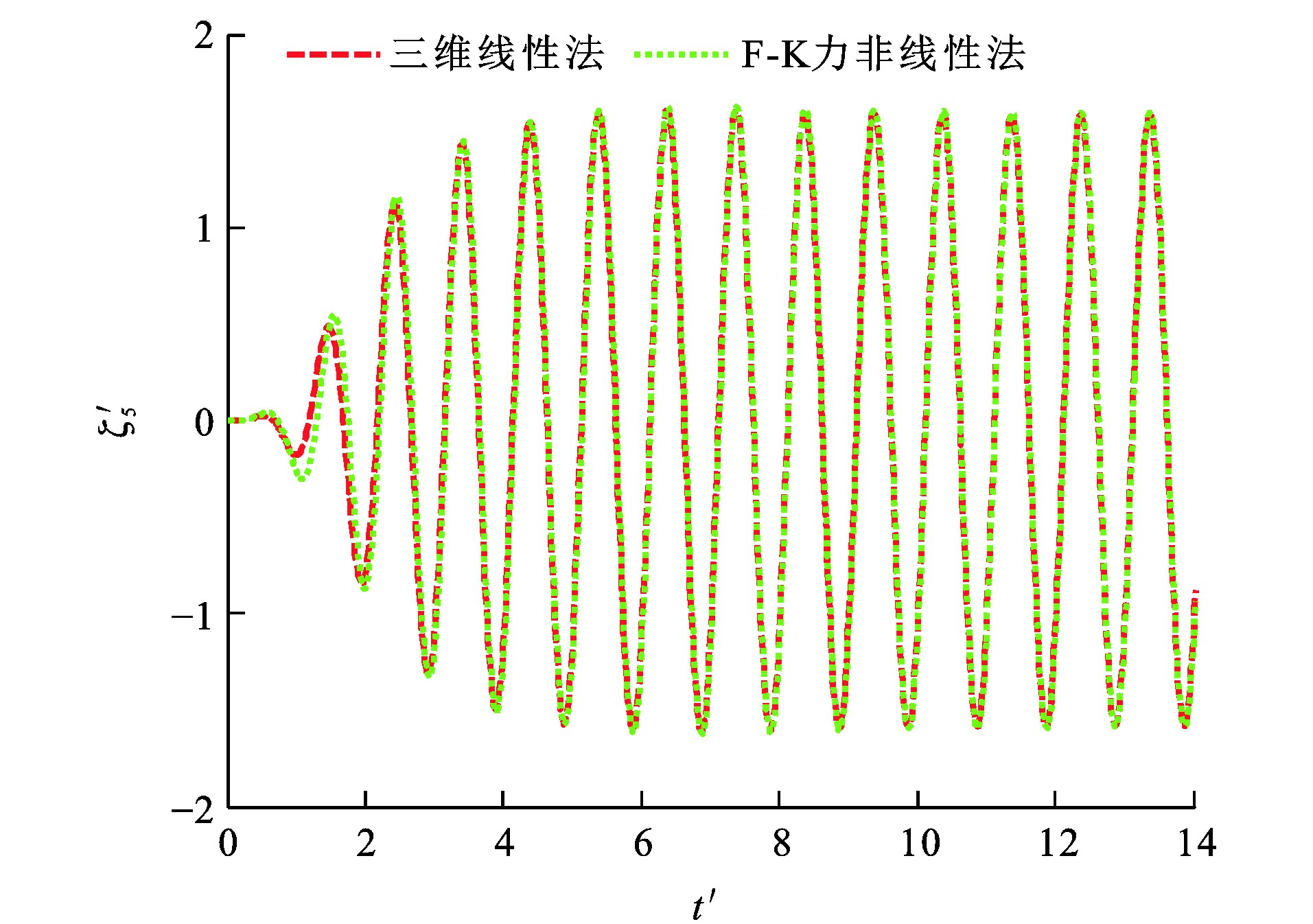
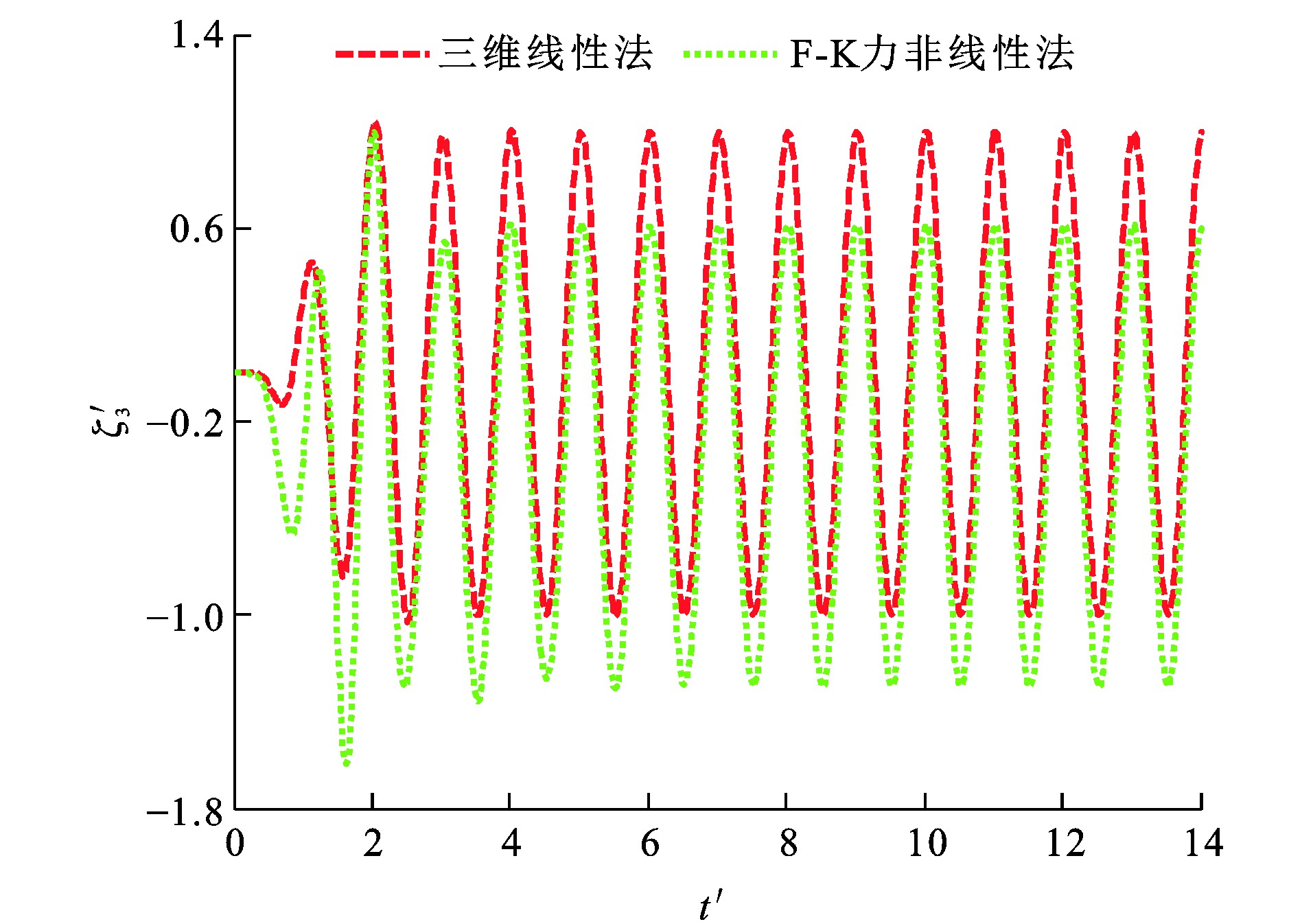
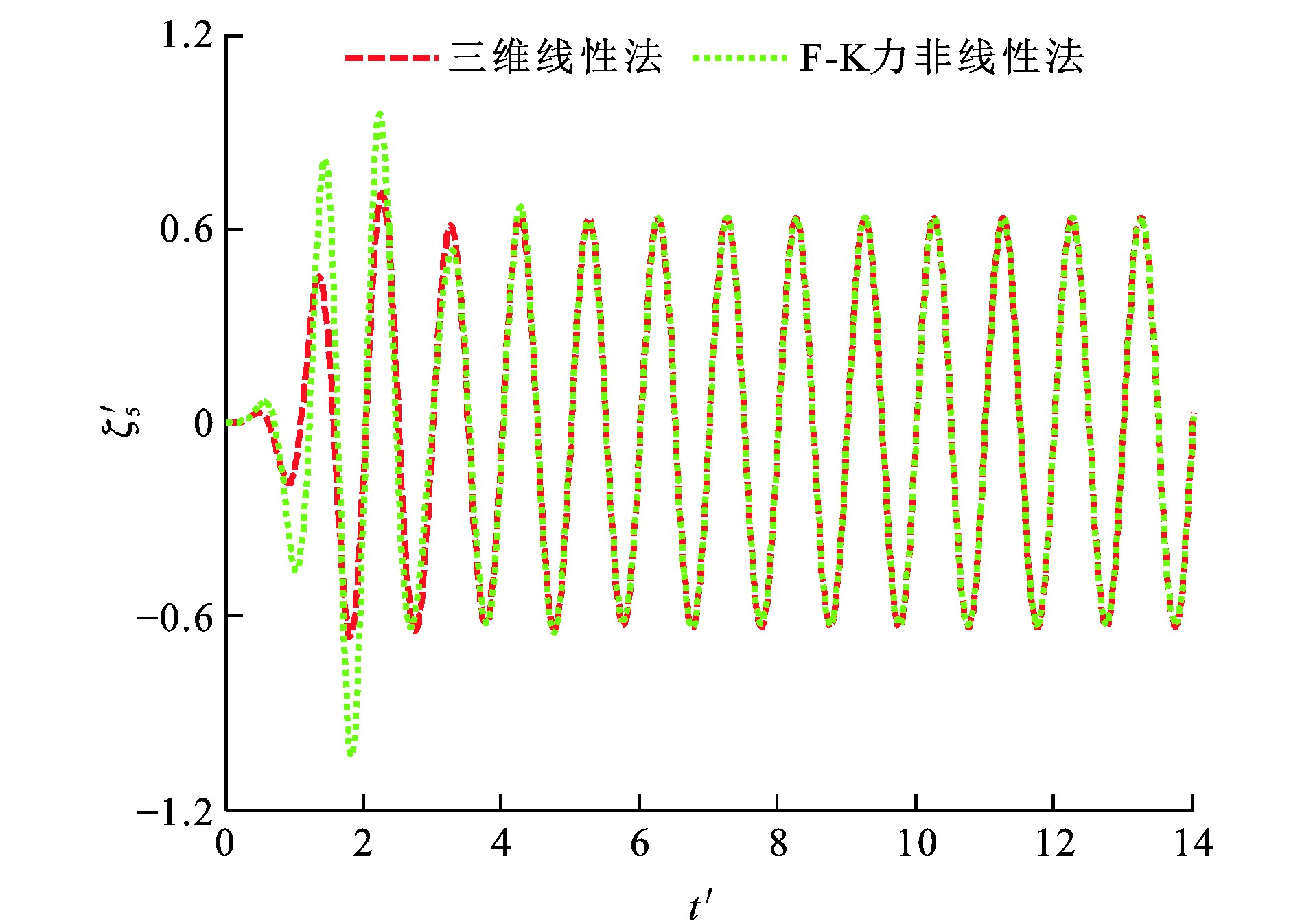
垂荡F-K力F_3I、纵摇F-K力F_5I、垂荡位移ζ₃、纵摇位移ζ₅和时间t的量纲一形式分别为F′_3I、F′_5I、ζ′₃、ζ′₅及t′^[29]。波浪参数设定: η₀为0.018 m; λ/L分别为1.25和2.00, 图 12~15为船舶垂荡与纵摇量纲一F-K力时历, 可知: 当λ/L为1.25时, 采用三维线性法所得垂荡F-K力幅值比F-K力非线性法的计算结果小33.8%, 而2种方法计算所得纵摇F-K力幅值相差小于1%;当λ/L为2.00时, 三维线性法所得垂荡F-K力幅值与纵摇F-K力幅值分别比F-K力非线性法的计算结果小19.1%与3.9%。

图  12  λ/L为1.25时的量纲一垂荡F-K力时历

Figure  12.  Time histories of non-dimensional heave F-K force when λ/L is 1.25

下载: 全尺寸图片 幻灯片

图  13  λ/L为1.25时的量纲一纵摇F-K力时历

Figure  13.  Time histories of non-dimensional pitch F-K force when λ/L is 1.25

下载: 全尺寸图片 幻灯片

图  14  λ/L为2.00时的量纲一垂荡F-K力时历

Figure  14.  Time histories of non-dimensional heave F-K force when λ/L is 2.00

下载: 全尺寸图片 幻灯片

图  15  λ/L为2.00时的量纲一纵摇F-K力时历

Figure  15.  Time histories of non-dimensional pitch F-K force when λ/L is 2.00

下载: 全尺寸图片 幻灯片

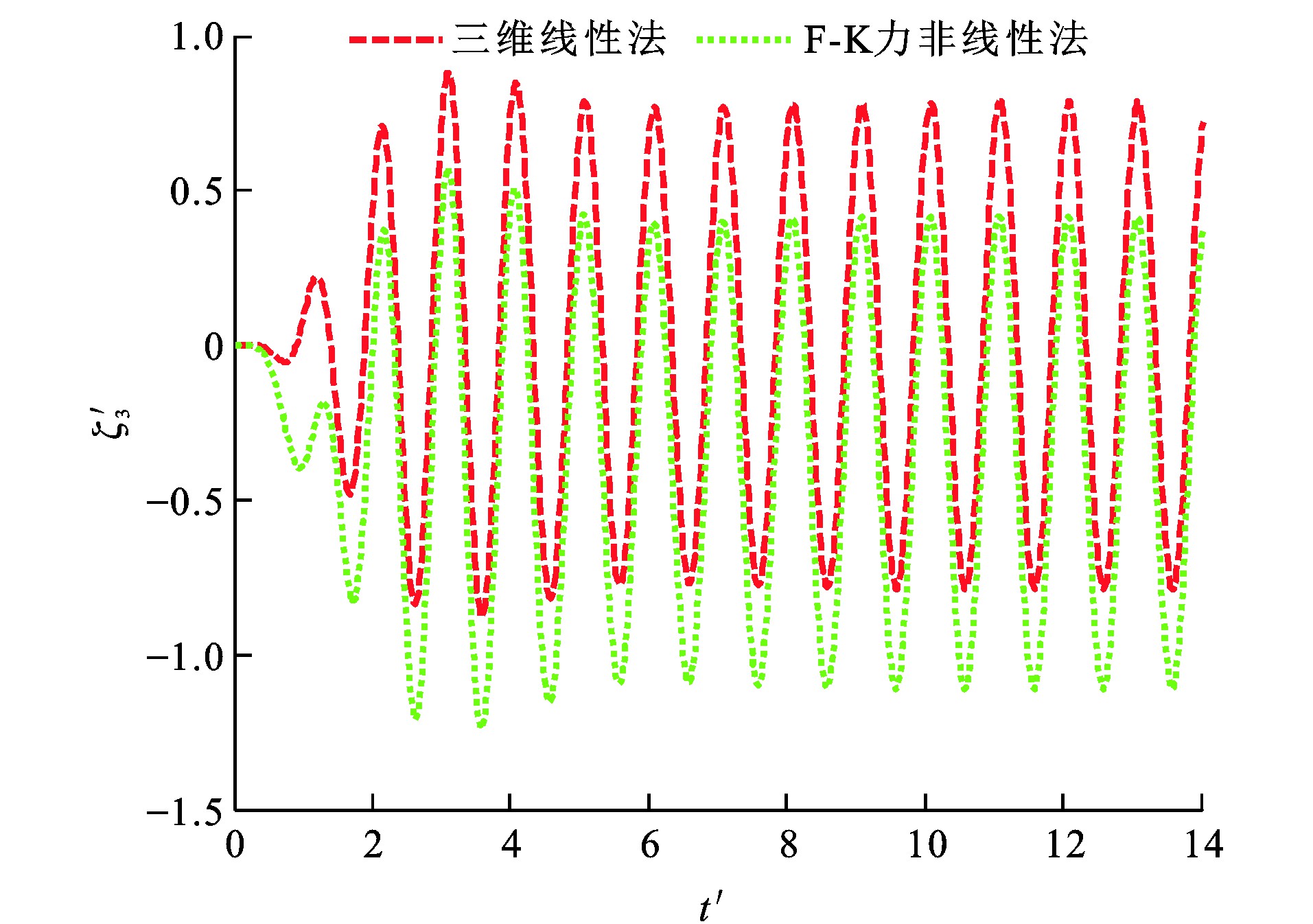
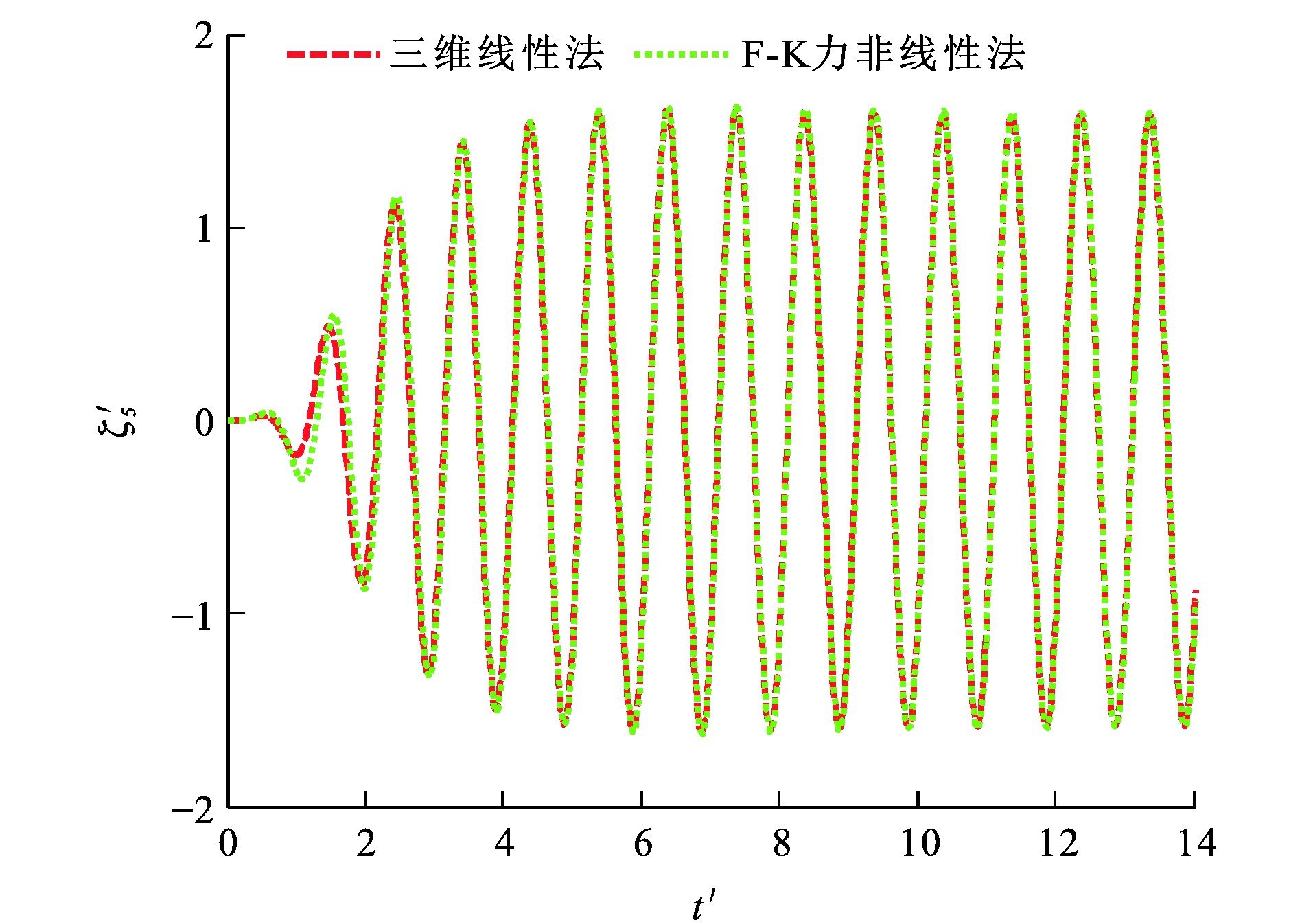
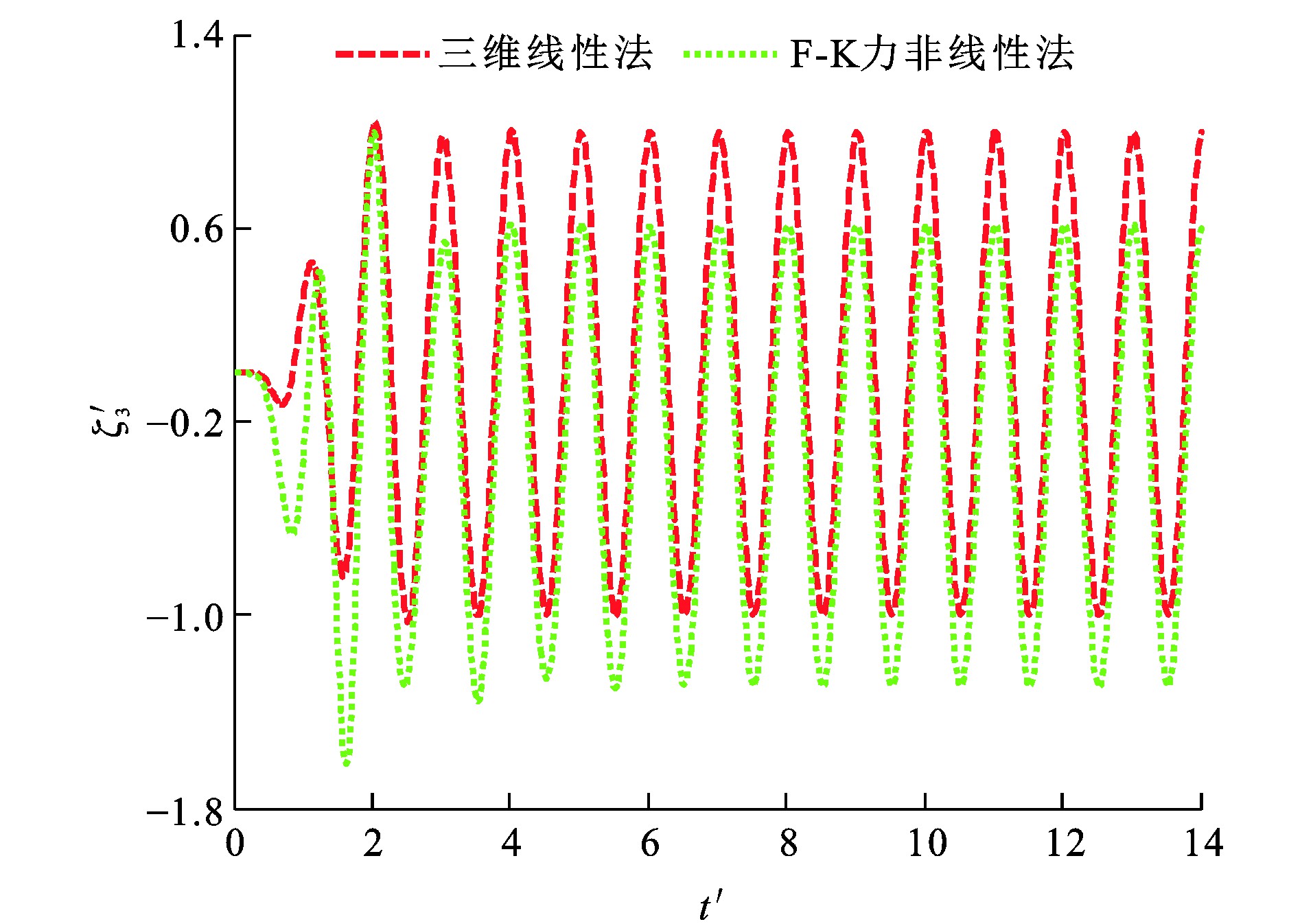
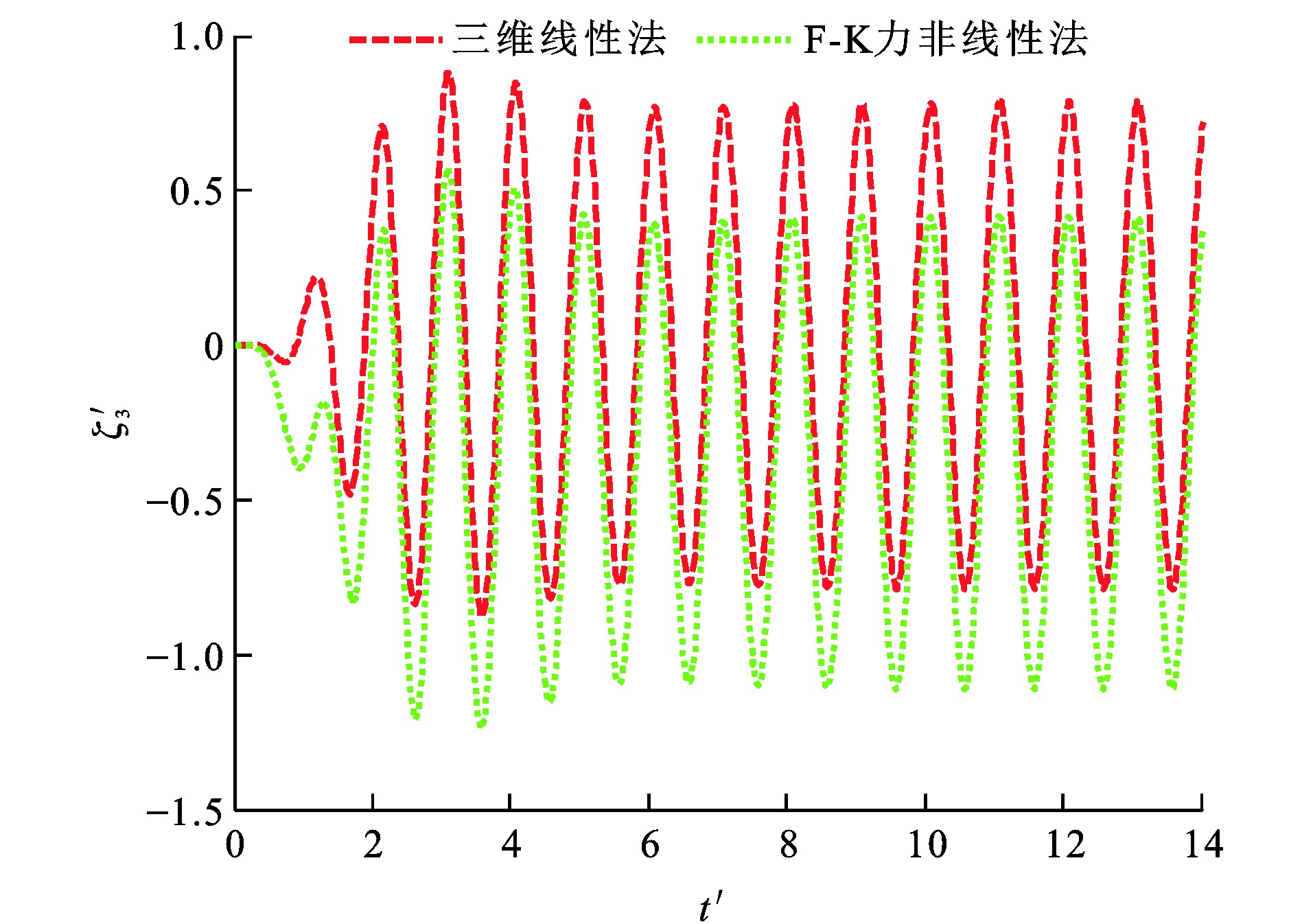
由于F-K力非线性法在船舶瞬时湿表面上计算F-K力, 而三维线性法在船舶平均湿表面上计算F-K力, 造成F-K力非线性法与三维线性法所得垂荡F-K力幅值计算结果相差较大。图 16~19为船舶垂荡、纵摇运动模态位移时历, 可知: 当λ/L为1.25时, 采用F-K力非线性法所得垂荡运动平衡位置较三维线性法向下移动约0.006 3 m; 当λ/L为2.00时, 采用F-K力非线性法所得垂荡运动平衡位置较三维线性法向下移动约0.006 0 m。

图  16  λ/L为1.25时量纲一垂荡运动时历

Figure  16.  Time histories of non-dimensional heave motion when λ/L is 1.25

下载: 全尺寸图片 幻灯片

图  17  λ/L为1.25时量纲一纵摇运动时历

Figure  17.  Time histories of non-dimensional pitch motion when λ/L is 1.25

下载: 全尺寸图片 幻灯片

图  18  λ/L为2. 00时量纲一垂荡运动时历

Figure  18.  Time histories of non-dimensional heave motion when λ/L is 2.00

下载: 全尺寸图片 幻灯片

图  19  λ/L为2. 00时量纲一纵摇运动时历

Figure  19.  Time histories of non-dimensional pitch motion when λ/L is 2.00

下载: 全尺寸图片 幻灯片

因为船体几何形状并不关于水线面对称, 且F-K力在船舶瞬时湿表面上进行数值计算, 引入物面及入射波引起的F-K力非线性因素影响, F-K力非线性法所得垂荡运动平衡位置相对于三维线性法向下移动一定距离。

3.4.2   船舶运动响应

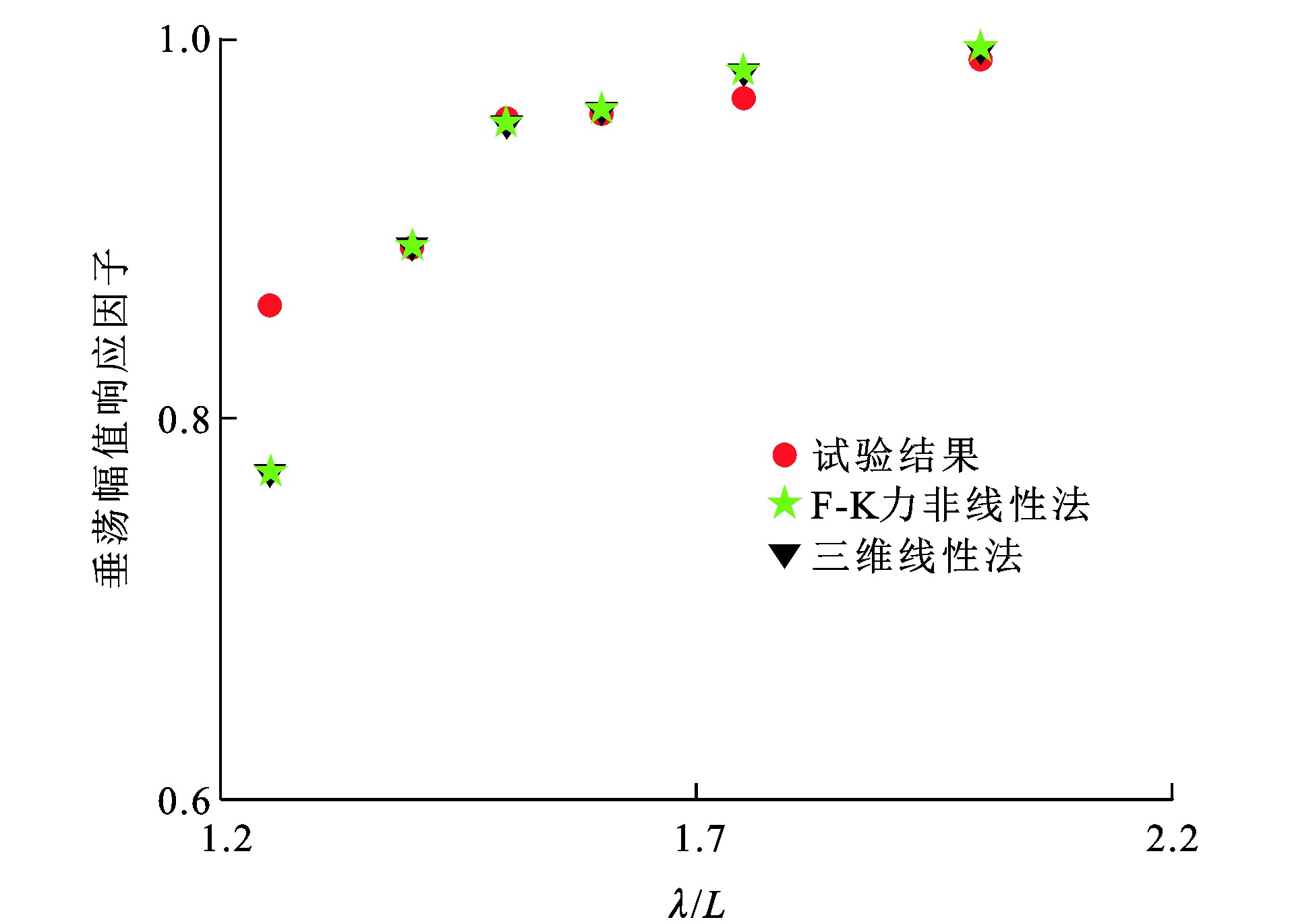
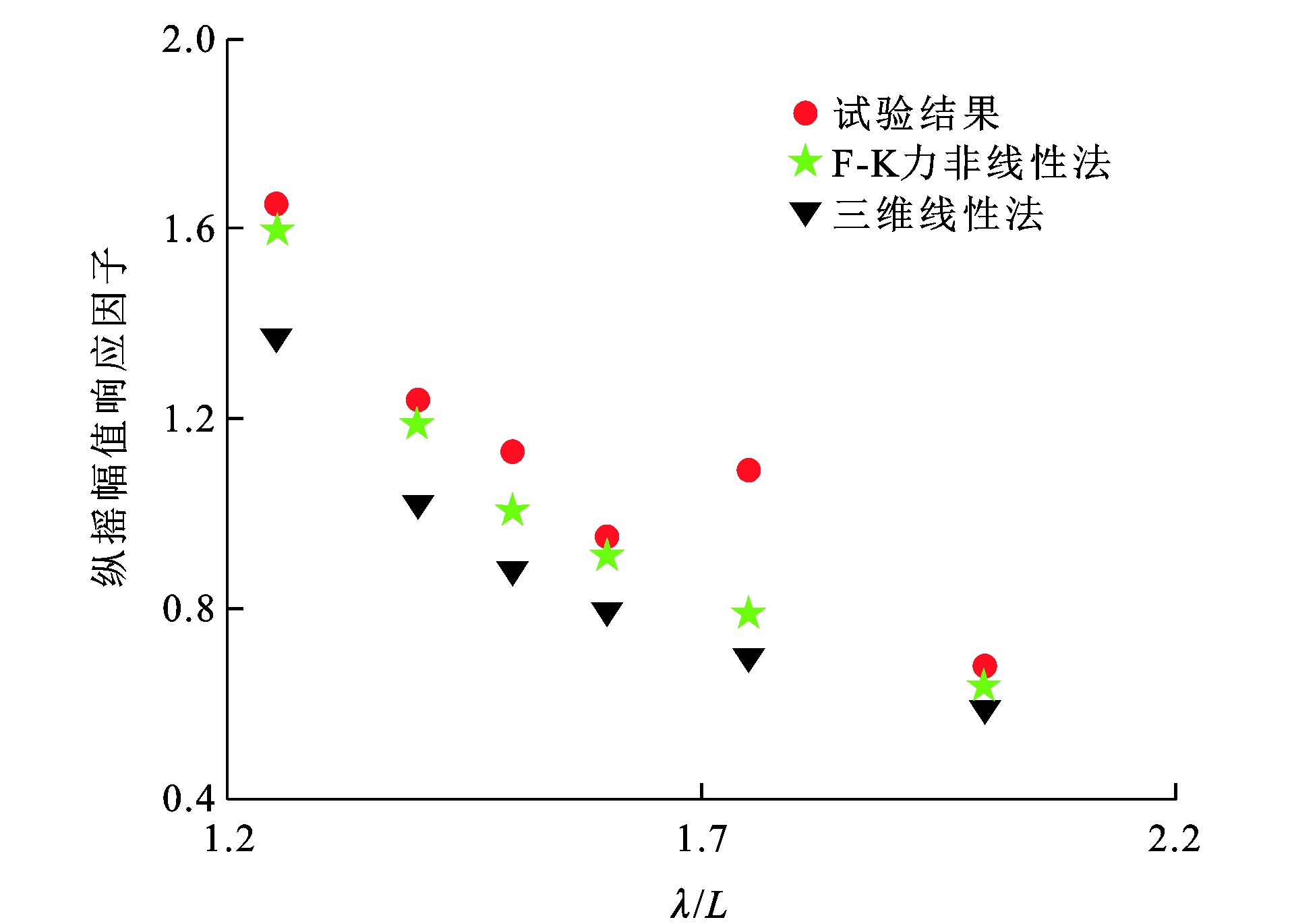
垂荡位移ζ₃的幅值响应因子为ζ_3a/η₀(ζ_3a为垂荡位移幅值), 纵摇位移ζ₅的幅值响应因子为ζ_5aL/(2πη₀)(ζ_5a为纵摇位移幅值)。图 20、21分别为Wigley Ⅰ型船舶垂荡与纵摇幅值响应因子, 可知: 对于垂荡幅值响应因子, F-K力非线性法与三维线性法^[31]所得计算结果与试验结果的相对误差都在10.4%以内; 而对于纵摇幅值响应因子, 除了λ/L≈1.75处, F-K力非线性法和三维线性法的计算结果与试验结果的相对误差分别在10.9%和22.0%以内, F-K力非线性法比三维线性法更接近试验结果, 且F-K力非线性法与三维线性法的垂荡幅值响应因子均与试验结果吻合较好; 对于纵摇幅值响应因子的数值预报, F-K力非线性法比三维线性法更接近试验结果; 对于纵摇幅值响应因子, 当入射波较长时, 其数值预报结果小于试验结果, 尤其当λ/L接近1.75时, F-K力非线性法与试验结果的相对误差为27.7%, 三维线性法与试验结果的相对误差为35.9%, F-K力非线性法和三维线性法均与试验结果相比有较大误差, 在该λ/L附近试验船舶运动响应幅值因子较大, 因为该频率与船舶的纵摇运动固有频率较为接近, 容易引起共振, 最终导致F-K力非线性法与三维线性法出现较大的计算误差。

图  20  垂荡幅值响应因子

Figure  20.  Heave response amplitude operators

下载: 全尺寸图片 幻灯片

图  21  纵摇幅值响应因子

Figure  21.  Pitch response amplitude operators

下载: 全尺寸图片 幻灯片

综上所述, F-K力非线性法较三维线性法对船舶运动建模具有更强的适用性。

4.   结语

(1) 针对经验公式、二维理论及三维线性理论对船舶运动数学模型建模适用性不强的问题, 在三维时域范畴内, 基于F-K力非线性法为航海模拟器建立了实用高效的规则波浪中船舶运动数学模型。

(2) 为减少由于瞬时自由面格林函数在自由液面处剧烈振荡增幅带来的计算误差, 舍去扰动速度势边界积分方程中的水线项, 除量纲一频率ω′≈1.7处, 舍去水线项计算所得水动力系数与试验值的最大相对误差为33.4%, 而未舍去水线项计算所得水动力系数与试验值的最大相对误差为54.8%, 舍去水线项计算所得水动力系数更接近试验结果。

(3) 由Wigley Ⅰ型船舶运动时历的计算结果可知, F-K力及船体几何形状非线性对船舶垂荡运动影响显著, 当λ/L为1.25时, 采用F-K力非线性法所得垂荡运动平衡位置较三维线性法向下移动约0.006 0 m。

(4) 对于纵摇幅值响应因子, 除了λ/L≈1.75处, F-K力非线性法和三维线性法所得计算结果与试验结果的相对误差分别在10.9%和22.0%以内, F-K力非线性法比三维线性法更接近试验结果, 因此, 本文所构建的规则波浪中船舶运动数学模型能极大地提高航海模拟器的行为真实感。

(5) 本文仅在规则波浪中基于F-K力非线性法对船舶运动进行建模, 下一步应将F-K力非线性法扩展到不规则波浪中船舶的运动建模研究, 为航海模拟器建立适用性更强的船舶运动数学模型。