-
摘要: 介绍了不完全驱动系统及其意义, 建立了船舶港内自动靠离泊模型和海上航运控制模型。以船舶在大洋航行或长距离转向点间航行中经常发生的直线轨迹跟踪为例, 运用输入-输出线性化设计方法, 给出了一个具有渐近跟踪能力的控制律。将该控制律应用于一个实例, 并用Matlab语言进行了计算机仿真, 结果表明该控制器可以解决船舶的不完全控制问题。Abstract: The underactuated system and its meaning were introduced. The automatic berthing control model and straight-line tracking control model for underactuated surface vessels were de-veloped. A state feedback controller that forces an underactuated ship to asymptolically track a straight-line was presented using the input-output linearization technique. This controller was ap-plied to an example, its control was simulated with Matlab software. The results show that this control strategy can resolve the control problems of underactuated ships.
-
船舶运动控制可概括为以下几种: ①船舶在航行中的自动导航问题, 包括航向控制、航迹跟踪控制等; ②船舶自动靠离泊问题, 涉及船舶在浅水中的低速运动, 风、浪、流干扰相对增大, 系统信息量增多, 控制难度极大; ③船舶自动避碰问题; ④船舶动力定位、高速船控制、船舶减摇鳍设计及舵阻摇控制等。由于船舶运动呈现大惯性、长时滞、非线性等特点, 且易受模型参数摄动及风、流、浪等外界干扰的影响, 又常常具有非完整约束和不完全驱动的特性, 不适用线性控制方法, 采用传统的控制策略更不能满足要求。常用的船舶运动控制策略包括: ①PID控制; ②自适应控制; ③变结构控制; ④具有自适应、自学习、自优化、自整定能力的智能控制, 其中又可分为神经网络控制、模糊逻辑控制、混合智能控制等。而许多文献中采用的这些方法大多针对线性系统, 有些虽然用于非线性系统, 但所得效果都不很理想。因此, 如何拓展其应用范围, 探索新的非线性控制策略, 已成为近年来船舶控制领域高度关注的一个焦点。
本文主要阐述了当前船舶运动非线性控制的不完全驱动系统控制器的设计, 介绍了非完整系统概念、不完全驱动系统的概念及其控制意义; 基于MMG分离建模思想提出了船舶自动靠离泊和航迹控制两种在不同情况下的不完全驱动船舶操纵运动数学模型, 为该类问题的后续研究打下基础; 并以船舶在大洋航行或转向点间航行中存在的直线轨迹跟踪实际问题为例, 基于重定义输出变量思想[1], 运用输入-输出线性化设计方法提出一种渐近跟踪控制律, 具体说明船舶在不完全驱动情况下的一种控制器设计方法; 同时以大连海事大学远洋实习船“育龙”轮为例, 利用Matlab语言进行了计算机仿真研究, 对本文所提出的控制器进行了验证。
1. 不完全驱动系统及其意义
1.1 完整约束和非完整约束[2]
定义1假定系统位形由q1、q2、…、qn, n个广义坐标规定, 并且存在k个独立的约束方程[2]

可以用这种方式表示的约束称为“完整约束”。如果系统受约束, 且约束方程都具有形如式(1)的完整形式, 则该系统称为“完整系统”。
定义2考察受有m个约束的系统, 如果这些约束为不可积分的微分表达式

式中: a为q和t的函数。这种约束称为“非完整约束”, 受有非完整约束的系统称为“非完整系统”。
对于非完整系统, 由于其微分方程的不可积性质, 不满足著名的Brockett必要条件[3], 不能转换成线性控制问题, 因而不能通过设计连续的时不变纯状态反馈控制律将其镇定到期望位姿上。对非完整系统控制方法[4]主要有3类: 光滑或者分段光滑的时变状态反馈控制器; 非连续的时不变状态反馈控制律; 混合控制律。
1.2 不完全驱动系统
定义3如果用于控制一个系统的控制向量所构成的空间维数少于该系统位形的空间维数, 则称这个系统为不完全驱动系统[5]。
简单地说, 不完全驱动系统就是指用于输入控制量数目少于系统本身自由度的系统。该类系统具有两个显著属性: 具有不可积的加速度约束关系和动态特性; 不能通过坐标变换转化成没有漂移的系统形式。因此, 具有二阶非完整约束则是对不完全驱动系统的另一常见描述(注: 一阶非完整约束是指对系统速度的约束; 二阶非完整约束是指对系统加速度的限制)[6]。
可见, 不完全驱动系统都受有非完整约束, 属于非完整系统。这要求在进行控制设计时, 要予以专门考虑, 探究新的控制策略, 才能达到预期的性能目标。研究对不完全驱动系统的控制问题, 不仅在理论研究上具有巨大的发展潜力, 在工程实际中更具有特殊的意义。首先, 一个不完全驱动系统实现了以较小数目的驱动器来完成复杂艰巨的任务, 不仅使成本大大降低, 重量减轻, 同时也会因控制设备的减少而降低机械故障的发生率, 使得系统运行更加稳定, 且易于维护。其次, 不完全驱动控制同时对完全驱动系统提供了一种备份控制技术。当一个完全驱动系统损坏时, 如果有预先备好的不完全驱动控制器随时可用, 那么就可以很从容地使失效系统很快恢复功能。对那些一旦控制器失灵便会导致灾难性后果的系统, 诸如飞机、宇宙飞船和大风浪中的水面船舶等, 这一点的意义非常重大。
正是由于上述原因, 对该课题的研究已经引起了控制界越来越多人们的关注。有关不完全驱动方面的文献最早见于1992~1995年针对机械手和航空器的控制设计; 1996、1997年开始被引用到船舶控制方面, 随后, 人们开始探索将各种技术应用于该领域[5~9], 其中最有代表性的文献[9], 提出了一种基于逻辑的混合控制策略, 解决了不完全驱动船舶自动靠泊难题; 而近期Jiang[1, 10, 11]等的成果又使不完全驱动船舶的控制研究取得了显著进展。
2. 不完全驱动船舶操纵运动数学模型
2.1 船舶港内自动靠离泊操纵数学模型
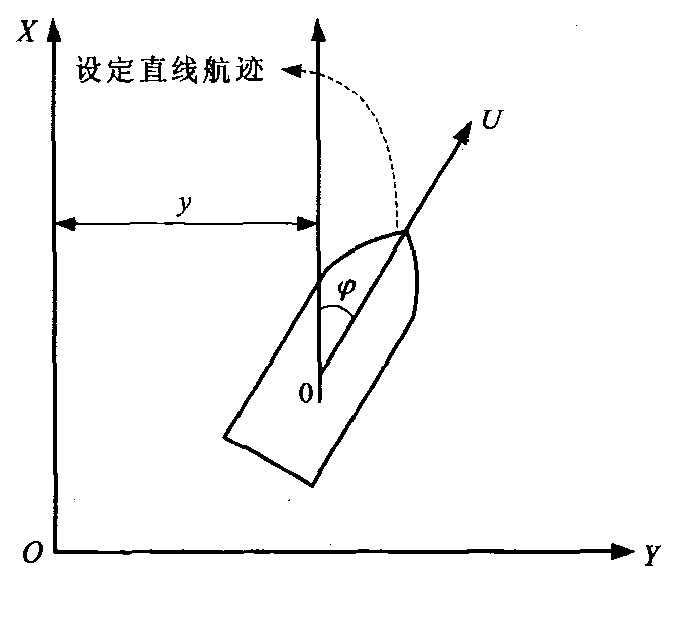
图 1为平面内船舶操纵运动坐标系统, 在这里作如下假设: ①随船坐标的原点与船舶重心重合; ②船体结构前后左右均对称; ③港内靠离泊操作一般都是在海况十分良好的条件下进行的, 故可以不考虑风、浪、流对船舶操纵的影响, 也暂不考虑锚、缆、船舶间相互作用等外力对船体的影响; ④由于船舶在港内靠离泊过程中处于低速运动状态, 舵已不能起到有效作用, 实际中采用拖轮、侧推器、锚、缆等来协助操船。本文假设在船舶前后对称位置装有两个侧推器, 且两个侧推器所产生的作用力大小相等, 方向相反, 并假定船舶在转船过程中不产生横移, 故侧推器只对船舶产生纯的转船力矩, 螺旋桨只在船舶纵向产生推力。由此引入平面内3自由度船舶运动数学模型[12]

式中: u、v、r分别为船舶的前进速度、横移速度和首摇角速度; x、y为船舶重心相对于固定(惯性)坐标系XOY中的坐标; φ为航向角; (x, y, φ)为系统的位形; m、mx、my、Izz、Jzz分别为船舶质量、附加质量、惯性矩和附加惯性矩; XH、YH、NH分别为作用于船体上的粘性流体动力和力矩; XP、YP、NP分别为螺旋桨产生的流体动力和力矩, 根据前述条件可知, YP、NP均为0;XST、YST、NST分别为侧推器产生的流体动力和力矩, 由前述推知, XST、YST为0。现将式(3)作如下变换

有关粘性流体动力和力矩的数学模型很多, 这里采用文献[12]中的线性模型

需要特别指出的是, (mx-my) uv为Munk力矩项, 仅为理论计算结果, 在船模试验时是不能分离出该项的, 体现在粘性力矩NH内。其他各项含义参见文献[12]。
将式(5)代入式(4), 得

式中:





最后, 经变换可得系统模型方程

从式(8)、式(9)不难发现子系统只有2个控制输入量, 且具有不可积的性质, 因此, 系统式(8)、式(9)是一个不完全驱动的、具有不可积约束的非完整系统。
2.2 船舶海上航迹控制数学模型
进行航迹控制时应同时考虑两方面: 航向控制和船位控制, 这里的船位控制是指对船舶偏离设定航迹线的横偏距离的控制。在大洋航行或长距离转向点航行中, 驾驶员的操船目标是使船舶尽可能沿着预先设定的直线航迹航行, 此时他们最关心的是横偏距离y和偏航角φ, 而不关心船舶沿航迹线的纵向位移x。为使问题简化, 本文假定航迹线与正北(X轴)重合, 见图 2。
在航迹控制过程中, 由于闭环反馈的控制作用使船舶运动变化在平衡状态附近, 此时船舶漂角较小, 作用于船舶上的流体力为线性的。不妨假设漂角可以忽略, 即有u > > 0, v≈0, 前进合速度



在实际中, 船舶直线运动经常呈现不稳定状态或临界稳定状态, 这时的船舶运动呈现非线性。本文考虑模型中非线性项的影响, 航向控制模型采用下列非线性动态模型[13]

式中: a1=1/T; a2=α/T, α为非线性项模型系数; b=K/T, K、T为船舶操纵性能指数。
根据上述分析, 将式(10)与式(11)组合, 略去式(10)中对船舶纵向位移x的考虑, 得到船舶直线航迹控制系统的非线性动态数学模型为

该系统同时具有非线性和不完全驱动的特性。
3. 实例分析
现在针对系统式(12), 设计出一个控制器δ使得(y, φ)趋近于零, 从而达到航迹控制目标。但是, 利用模型式(12)的一个明显困难是输出(y, φ)与控制输入不在一个通道, 仅仅通过状态变量及非线性状态方程式(12)与控制输入有关, 不易进行控制器设计。然而, 受文献[14]启发, 采用输入-输出线性化方法可以得到输入-输出的直接而简单的关系, 从而降低控制设计的困难。
为对系统式(12)进行输入-输出状态反馈线性化控制器设计, 需构造一个系统输出函数。这里定义z为y和φ的组合输出变量, 即

式中: k > 0, k为设计参数。为得到线性输入-输出关系, 对式(13)中输出函数z进行第一次微分

此时, 输入u没有出现, 需继续对ż进行微分

此时输入δ被导出。由此可以看到: 通过重定义输出变量式(13), 利用输入-输出线性化方法, 得到了输入-输出间的线性关系, 这时设计控制器就容易了。
为使系统式(15)稳定, 消去其中的非线性项和不稳定项, 取如下控制律

式中: k1、k2都是大于零的实数, 是由设计者选择的线性增益, 对其选择可以使下列方程

的根具有负实部。
将控制律式(16)代入式(15), 可得到闭环系统

由式(17)可见, 该闭环系统是稳定的。运用Lyapunov稳定性定理不难证明, 控制律式(16)是系统式(15)的全局渐近稳定(GAS)控制律。
由式(13)可以得φ=z-ky, 代入式(12)中的第一个方程, 得

取Lyapunov预选函数V=y2/2, 当控制律式(16)使z=0, 沿式(19)的轨迹对其求导

取k < 0.5π/|y0|, y0为初始横偏距离。在实际控制过程中, 开始时可能会因船舶的惯性而出现较小的“反横距”(在满舵时, 反横距约为船宽的1~1.5倍), 但必有|y| < 2|y0|, 则

因而有

当且仅当y=0时, ˙V=0。由Lyapunov稳定性理论可知, 系统式(22)是渐进稳定的。由于k的选取与初始值y0有关, 因而是局部渐进稳定(LAS)的, 从而y也是局部渐进稳定的。
以大连海事大学远洋实习船“育龙”号为例进行航迹控制设计。该船船长L为126 m, 船宽B为20.8 m, 满载吃水d为8.0 m, 方形系数Cb为0.681, 船速U为7.7 m/s; 通过计算得K=0.478, T=216;取α=30;各设计参数相应取为k=0.001, k1=0.002, k2=0.15时, 代入式(16)并经转换得船舶航迹控制律算法为

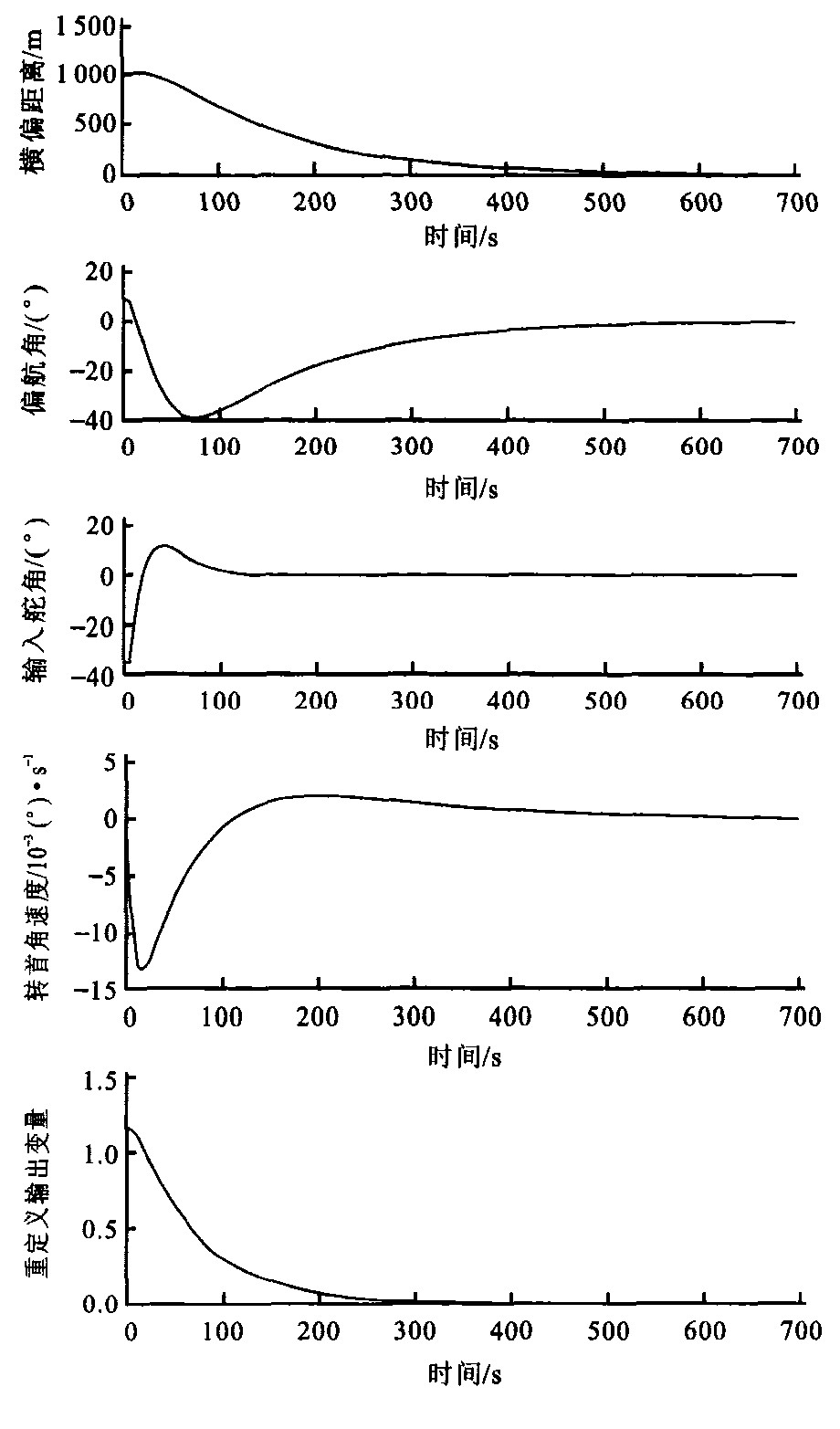
取初始值y0=1 000 m, φ0=10°, 用Matlab Simulink软件进行仿真, 结果见图 3。
从仿真结果图 3可以看出, 船舶的横偏距离y和偏航角φ在只有一个控制输入舵角δ的作用下, 是可以达到渐近稳定的。仿真结果表明, 本文针对不完全驱动系统式(12)所提出的控制器是十分切实有效的。
4. 结语
本文介绍了不完全驱动船舶的非线性控制问题, 建立了两个适于研究不完全驱动船舶的操纵数学模型——港内自动靠离泊模型和长距离直线航行中的航迹控制模型, 以船舶直线航迹控制的实际问题为例, 运用输入-输出线性化设计方法提出一个具有渐近跟踪能力的控制律, 具体说明了船舶在不完全驱动情况下的一种非线性控制设计方法; 并以大连海事大学远洋实习船“育龙”号为例, 进行了计算机语言仿真研究, 对本文所提出的控制器进行了验证, 结果表明, 该系统及所采用的控制策略可以适用于解决船舶不完全驱动控制问题。
-
[1] Do K D, Jiang Z P, Pan J. Underactuated ship global tracking under relaxed conditions[J], IEEE Transactions on Automatic. Control, 2002, 47(9): 1529-1536. doi: 10.1109/TAC.2002.802755 [2] [美]格林伍德. 经典动力学[M]. 北京: 科学出版社, 1982. [3] Ryan E P. On brockett's condition for smooth stabilizability and its necessity in a context of nonsmooth feedback[J]. Journal of Control Optimization, 1994, 32(6): 1597-1604. doi: 10.1137/S0363012992235432 [4] Kolmanovsky I V, McClamroch N H. Developments in non-holonomic control problems[J]. Control Systems Magazine, 1995, 15(6): 20-36. [5] Reyhanoglu M. Exponential stabilization of an underactuated autonomous surface vessel[J]. Automatica, 1997, 33(12): 2249-2254. doi: 10.1016/S0005-1098(97)00141-6 [6] Tsiotra P. Invariant manifold techniques for control of underactuated mechanical systems[R]. Proceedings of the American Control Conference, 1997. [7] Francesco Bullo, Naomi Ehrich Leonard. Control lability and motion algorithms for underactuated lagrangian systems on lie groups[J]. IEEE Transactions Automatic Control, 2000, 45 (8): 1437-1454. [8] Indiveri G, Aicardi M. Nonlinear time-invariant feedback control of an underactuated marine vehicle along a straight course[A]. Proc. of the IFAC Conference on Manoeuvring and Control of Marine Craft[C]. MCMC 2000, Aalborg, Denmark, 2000. [9] Tae-Han Kim, Tamer Basar, In-Joong Ha. Asymptotic stabilization of an underactuated surface vessel via logic-based con-trol[R]. Proceedings of the American Control Conference, 2002. [10] Jiang Z P. Global tracking control of underactuated ships by Lyapunov's direct method[J], Automatica, 2002, 38 (2): 301-309. doi: 10.1016/S0005-1098(01)00199-6 [11] Do K D, Jiang Z P. Robust global stabilization of underactuated ships on a linear course: state and output feedback[J]. International Journal of Control, 2003, 76(1): 1-17. [12] 贾欣乐, 杨盐生. 船舶运动数学模型[M]. 大连: 大连海事大学出版社, 1999. [13] 杨盐生. 不确定系统的鲁棒控制及其在船舶运动控制中的应用[D]. 大连: 大连海事大学, 2000. [14] Shankar Sastry. Nonlinear Systems: Analysis, Stability and Control[M]. New York: Springer-Verlag, 1999. -






 下载:
下载:



 下载:
下载: