Calculation model of maximum number for gathering passenger at railway passenger station
-
摘要: 考虑了旅客出行习惯和列车晚点, 建立了铁路客运站旅客最高聚集人数计算模型。在模型中, 在出行时, 乘坐6:00~9:00出发列车的旅客一般在列车出发前5~60 min到达客运站, 乘坐21:00以后出发列车的旅客一般在19:00~21:00达到客运站; 在晚点调整时等级越高的列车具有越高的优先权, 晚点时间与运行时间成正比。计算结果表明: 考虑出行习惯后, 计算的旅客高峰时段与实际调查结果相符, 考虑列车晚点后, 旅客最高聚集人数超出未晚点时的50%, 因此, 建议客运站的最高聚集人数设计系数为1.3~1.8, 并按行车密度从小到大取值。Abstract: Based on considering passenger trip habits and train delays, a computation model of maximum number for assembling passengers at railway passenger station was proposed. In the model, when trains' departure times were between 6:00-9:00, passengers reached railway passenger station in advance 5-60 min. When trains' departure times were after 21:00, passengers reached railway passenger station at 19:00-21:00. The higher train grade was, the higher its priority of delay adjustment was. The delay time was direct proportion to the running time. Computation result shows that under considering passenger trip habits, the computation period of time for maximum number of assembling passengers accords to the actual period of time. Under considering train delays, the maximum number of assembling passengers increases by above 50%. So, the design coefficient of the maximum number are suggested, its value should vary from 1.3 to 1.8 when the change of running density of trains varies from small to big.
-
0. 引言
铁路客运站旅客最高聚集人数是由于旅客在某一时间内集中到达而使客运站人数在某一时刻达到很大而产生的, 是铁路客运站设计的重要指标, 与站房规模、投资数量、各相关配套用房的设置紧密相关, 故其准确性十分重要。由旅客运输组织过程可知, 影响旅客最高聚集人数的因素有旅客列车在客运站上车人数、旅客列车开行列数、列车发车间隔、检票起始和结束时间以及旅客在客运站候车时间等。上述因素中除最后一个因素以外都可由铁路部门控制, 影响旅客在客运站候车时间的因素有很多, 其中主要为旅客出行习惯和列车晚点。马卫武等通过现场调研的方式对旅客候车时间进行专门研究, 但未考虑旅客在1 d内不同时段具有不同出行习惯[1]; 何宇强等主要从铁路部门可控因素着手对最高聚集人数和既有站旅客最高聚集人数计算进行研究, 在综合分析相关因素后提出模拟计算法、概率统计法和最坏情景法, 对一些参数的取值进行确定与说明, 并将结果与现实数据进行比对[2]; 张天伟等重点研究设计期客运站最高聚集人数预测模型, 通过实地调研分析旅客到达规律与出发规律, 进而形成聚集规律, 并利用研究结果对新广州站旅客最高聚集人数进行预测[3-4]。上述文献在计算旅客最高聚集人数时均未考虑旅客出行习惯和列车晚点, 对铁路旅客进行大量调查后认为旅客在不同时段具有不同出行习惯, 虽有提及, 但均未做深入探讨。
本文通过相关调研, 认为乘坐9:00之前出发列车的旅客考虑起床和早餐等因素后到达客运站一般较为密集, 而乘坐21:00以后出发列车的旅客考虑晚餐、到达客运站距离、城市公共交通状况等因素后到达客运站一般较为分散。列车晚点将导致旅客在客运站停留时间增加, 这将导致旅客在客运站实际候车时间增加, 影响旅客聚集人数。影响列车晚点因素较多, 如客运站通过能力、客运站到达与出发线路使用情况、施工天窗选取时间及长短、列车运行图抗干扰能力与晚点调整措施等[5-15], 故列车晚点具有很大随机性。本文在现有研究成果基础上, 重点研究考虑出行习惯和列车晚点的旅客最高聚集人数计算模型。
1. 计算模型
1.1 基于出行习惯的到达人数计算模型
设i为1 d内出发列车的序号; m为1 d内客运站出发列车总数; tzi为第i列列车在客运站的正点出发时刻, 取铁路实际运营时刻(精确到min) 0:00、0:01、0:02、…、23:59、24:00, 下文中有关时刻参数的说明均与此相同; 为计算方便, 特规定列车序号按照出发时刻由早到晚顺序排列, 若有出发时刻相同的列车, 按i、i+1、…排列; Ni为第i列列车在客运站的定员; αi为第i列列车在客运站的满座率, 一般在0.7~1.3之间; βi为第i列列车送客人数占上车人数的比例, 一般在0~0.3之间。
乘坐第i列列车的旅客应在时刻区间[tzi-Tfi, tzi-Tli]内到达客运站, 其中Tfi和Tli分别为乘坐第i列列车的第1名和最后1名旅客到达客运站时距离所乘坐列车正点出发时刻的时间段。k时刻乘坐第i列列车到达客运站的人数Aki为
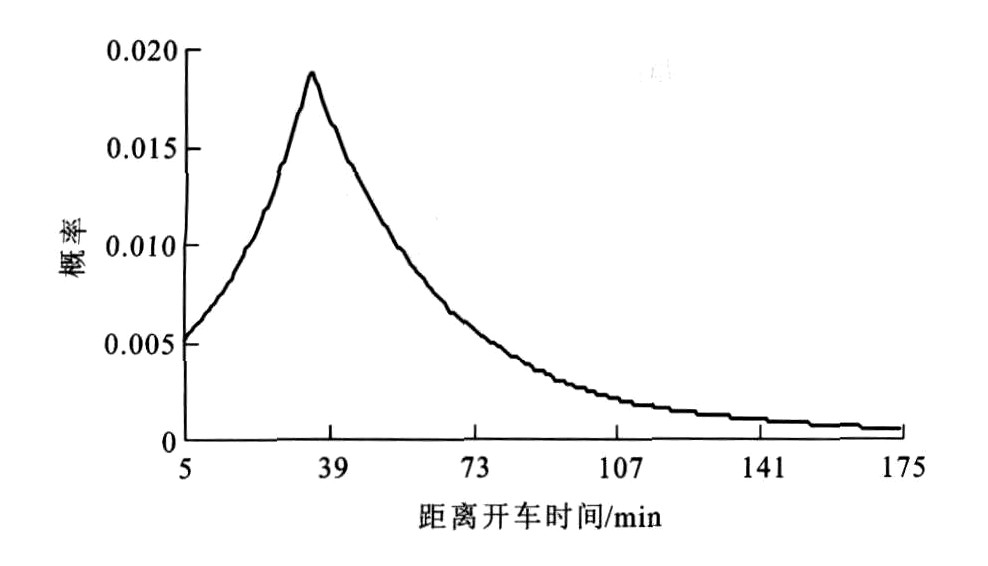
Aki={Νiαi(1+βi)∫Τfi-Τlitzi-Τli-kγg(Τ)dΤk∈[tzi-Τfi,tzi-Τli]0k∉[tzi-Τfi,tzi-Τli] (1) g(Τ)=0.001363e-[(Τ-34.45)/2.03]2+0.010350e-[(Τ-39.94)/14.12]2-0.0006494e-[(Τ-27.20)/5.50]2-0.004484e-[(Τ-45.89)/10.29]2+0.003125e-[(Τ-30.46)/25.00]2-0.001760e-[(Τ-40.89)/6.65]2+0.002001e-[(Τ-54.09)/101.90]2+0.005905e-[(Τ-43.26)/40.76]2 (2)
式中: γ为调整系数; g (T) 为旅客到达客运站的分布密度函数; T为旅客列达客运站的时刻距离列车开车时刻的时间段。
本文在文献[1]的基础上, 修正Tfi和Tli的取值。式(2) 反映的旅客到达概率分布见图 1。因现有列车定员一般不超过1 400人, 由于很多客运站都是在开车前5 min停止检票, 故本文对旅客到达也取到开车前5 min; 同时假定距离开车时间大于175 min时, g (T) 为0。
由图 1可知, 检票结束时, 仍有旅客到达, 即
∫1755g(Τ)dΤ=0.928<1
该分布不能保证所有旅客在规定时间内到达。通过调研, 本文认为乘坐6:00~9:00出发列车的Tfi和Tli可分别近似为60 min和5 min, 乘坐9:00~21:00出发列车的Tfi和Tli可分别近似为175 min和5 min, 乘坐21:00以后出发列车的Tfi和Tli分别为近似为大于175 min和5 min。尽管对时段的划分也是根据相关调研和旅客出行习惯选定, 但存在进一步细化的必要。由于
∫605g(Τ)dΤ=0.650
即该分布不能保证所有旅客在规定时间内全部达到, 修正γ取值, 建议为
γ={10.650tzi∈(6:00,9:00]10.928tzi∈(9:00,19:00]1.10.928tzi∈(19:00,21:00]10.928tzi∈(21:00,6:00] (3)
1.2 基于列车晚点的出发人数计算模型
由文献[3]可知: 在检票开始阶段, 由于旅客聚集较多, 一般以恒定速度通过检票口; 而后检票速度迅速下降, 且此后到达的旅客直接通过检票口, 很难形成旅客聚集, 所以本文对旅客离开客运站行为作匀速运动处理。
令tsi为1 d内第i列列车在客运站的实际出发时刻, 根据中国铁路实际情况, 大多存在tsi≥tzi; 令
ξi=tsi-tzi
为第i列列车晚点时间段, 其分布函数F (ξi) 为
F(ξi)={g0ξi=0g0+g1∫ξi0ne-ntdtξi∈(0,Τw)1ξi=Τw (4)Τw=δΤr (5)
式中: g0为列车正点到达概率; g1为晚点列车数占所有运行列车数的比例, 根据大数定律可知在列车数量很多的条件下, g1可以近似等于列车晚点概率, 故有g0+g1=1;t为时间; n为待定参数; Tw为列车到达客运站时理论最大晚点时间; Tr为列车从始发站正点运行到客运站时需要的时间长度, 一般认为始发列车不晚点, 实际由于车底套用使得始发列车晚点也时有发生, 故对列车晚点还需进一步研究; δ为比例参数, 建议根据列车等级取0~0.3。
由于式(4) 不能保证
g0+g1∫ξi0ne-ntdt=1
故Tw不可能为¥, 故在具体应用时需要对参数n进行合理取值, 以使式(4) 成立。
令Tji为第i列列车检票时刻距离列车实际出发时刻的时间段, 一般取20~30 min; 令tsi-Tji为第i列列车检票开始时刻。此时, 所有乘坐第i列列车的乘客中已经到达的人数为Api, 其中时刻为
p=min{tsi-Τji,tzi-Τli}
令vj为匀速检票速度, 第i列列车在区间[tsi-Τji,tsi-Τji+Apivj]内匀速检票, 考虑到检票过程中还有旅客到达客运站, 故将上述时刻区间修正为[tsi-Τji,tsi-Τji+Aqivj], 其中时刻为
q=min{tsi-Τji+Apivj,tzi-Τli}
令xki为0-1变量, 当k∈[tsi-Τji,tsi-Τji+Aqivj]时, xki=1, 否则xki=0。故在k时刻通过检票口从客运站出发的旅客人数Dk为
Dk=m∑i=1xki(k-tsi+Τji)vj (6)
1.3 旅客最高聚集人数计算模型
在k时刻客运站的聚集人数Hk为
Ηk=m∑i=1Aki-Dk (7)
客运站旅客最高聚集人数H为
Η=λmaxk{Ηk} (8)
式中: λ为修正系数, 根据客流波动情况, 取1.2~1.7。
2. 计算结果分析
利用计算模型计算旅客最高聚集人数的难点在于i、m、tzi等变量的确定, 这些值在客运站修建之前不可能得到, 只有在列车运行图编制完毕后才能确定, 而且还会因运行图的差异而不同; 但设计期应有日出发列车数、最小发车间隔、始发列车定员、过路列车定员等参数估值, 可结合上述数据与一些经验取值计算, 文献[2, 3]就是使用该思路预测客运站旅客最高聚集人数。根据郑州火车站的实际情况, 结合文献[2, 3, 4]]和相关经验数据对相应参数取值如下: m为161列(郑州站实际发出列车数为231列, 但考虑0:01~5:59之间出发70列列车为过路列车, 定员较少, 不会形成旅客最高聚集人数, 故取161列)。按照最新列车运行时刻表可知, tz1为6:00, tz2为6:06, …, tz161为23:57;始发动车的定员和上座率分别为1 220人和0.8;始发特快列车的定员和上座率分别为1 200人和1.0;始发直通快速列车的定员和上座率分别为1 200人和1.0;始发管内快速列车的定员和上座率分别为1 200人和0.8;始发直通普快列车的定员和上座率分别为1 200人和1.0;始发管内普快列车的定员和上座率分别为1 200人和0.8;过路列车不分等级, 定员为管内400人、直通200人, 上座率均取1.0。由于郑州站未有直快、管内始发动车、管内始发特快与普慢列车, 本文未予考虑。所有列车β为0.3, λ为1.6;Tfi为60 min (i=1, 2, …, 28), Tji为175 min (i=29, 30, …, 161);Tli为5 min (i=1, 2, …, 161);vj为90人·min-1; Tj的取值分两种情况, 始发列车取30 min, 过路列车取20 min; δ按照车型取值, 动车取0, 特快列车取0.04, 快速列车取0.08, 普快列车取0.10。
2.1 考虑出行习惯的情况
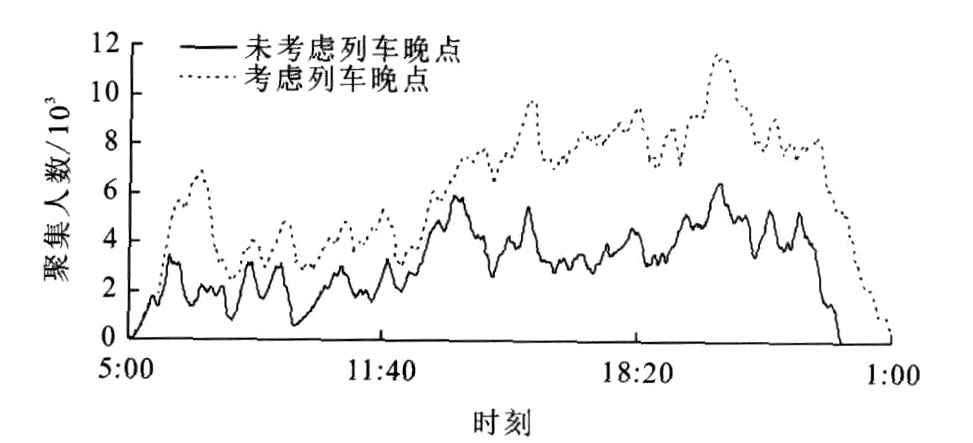
旅客出行习惯对旅客聚集的影响见图 2。由图 2可知, 未考虑出行习惯时乘坐6:00出发列车的第1名乘客在3:06到达客运站, 与实际情况不符; 相关数据为: H6:03为5 871人, H13:33为5 894人, H20:27为6 196人, 考虑客流波动后认为在20:27取得旅客最高聚集人数, 为9 914人, 但6:03出现的聚集高峰在实际调查时并未出现。考虑出行习惯后, 由计算结果可知最大值H20:24为6 481人, 此时旅客最高聚集人数为10 361人; 在6:00附近并未出现聚集高峰, 与实际调查情况符合。图 2中, 在8:38~16:23、20:43~23:41两个时段内两曲线重合, 认为考虑出行习惯后, 上述两个时段计算结果较符合实际。
考虑出行习惯后, 在6:00~9:00时段内旅客到达密集反而没有出现聚集高峰是因为在检票开始时到达客运站的旅客占所有旅客的比例不同, 未考虑出行习惯时, 始发与过路列车到达比例分别为
∫17531g(Τ)dΤ/0.928=0.736∫17521g(Τ)dΤ/0.928=0.875
考虑出行习惯之后, 两者比例分别为
∫6031g(Τ)dΤ/0.650=0.357∫6021g(Τ)dΤ/0.650=0.851其中∫3021g(Τ)dΤ/0.650=0.494 (9)
式(9) 表明近50%旅客在开车前21~30 min到达, 且检票开始后旅客数量将迅速下降, 而后到达客运站的旅客大多数直接通过检票口, 故很难形成聚集高峰; 尽管考虑出行习惯后过路列车在检票开始时到达比例为0.851, 由于过路列车定员较少, 故也很难形成聚集高峰。
2.2 考虑列车晚点的情况
由于列车晚点时间不同将带来不同组合, 本文仅计算εi=Tw/2时的情况。在考虑出行习惯的基础上, 列车晚点对旅客聚集的影响见图 3。
由图 3可见, 考虑列车晚点因素后旅客聚集最大值H20:20为11 699人, 此时旅客最高聚集人数为18 718人, 与未考虑列车晚点之前的10 361人相比增加了近80%。根据实际调研可知, 计算值18 718人偏大, 主要原因是对列车晚点采取了结果偏大的处理方式, 比如1352/1353次列车晚点为4.4 h, 共有41列列车晚点在1 h以上。这表明乘坐这些过路列车的旅客不得不额外在客运站停留1 h以上, 故使计算结果偏大; 若取ξi=Tw/3甚至更小则可有效降低最高聚集人数。
经过晚点处理后会出现同一方向列车出发时间不满足列车追踪间隔时间要求的情况, 考虑到过路列车定员较少且实际运营中不会出现; 仅计算6:00~24:00之间出发的列车, 考虑晚点后会出现这一时段实际出发的列车与运行图安排有所不同, 可能会带来计算结果的不同。但考虑到列车晚点后实际出发时刻进入这一时段的列车应为6:00之前出发的列车, 其定员较少, 不会对最终结果产生实质性的影响, 故本文计算时未详细讨论上述2种情况。
3. 结语
从对郑州火车站的最高聚集人数计算结果可知, 考虑出行习惯和列车晚点后将会导致实际旅客最高聚集人数增加, 根据实际情况建议客运站设计时可在原来基础上增加比例系数1.3~1.8, 按照行车密度从小到大对比例系数也从小到大取值; 因行车密度较小时旅客到达叠加不严重, 且列车晚点时较易调整, 行车密度较大时恰好相反。本文对旅客出行习惯以及列车晚点缺乏较深入的研究, 导致某些处理方式值得商榷。但在现有文献基础上, 考虑出行习惯和列车晚点因素后对旅客最高聚集人数计算模型进行研究, 拓宽了研究思路, 丰富了研究内容。从对郑州火车站所作的计算结果可知, 考虑上述2点因素后的计算结果更加符合实际。另外, 文中部分参数的取值也需根据铁路客运最新资料和发展方向做进一步修正。
-
[1] 马卫武, 刘小燕, 李立清, 等. 铁路客运站旅客候车时间研究[J]. 铁道学报, 2009, 31 (5): 104-107. doi: 10.3969/j.issn.1001-8360.2009.05.017MA Wei-wu, LIU Xiao-yan, Li Li-qing, et al. Research of waiting time of passengers at railway stations[J]. Journal of the China Railway Society, 2009, 31 (5): 104-107. (in Chinese) doi: 10.3969/j.issn.1001-8360.2009.05.017 [2] 何宇强, 毛保华, 陈绍宽, 等. 铁路客运站最高聚集人数计算方法研究[J]. 铁道学报, 2006, 28 (1): 6-11. doi: 10.3321/j.issn:1001-8360.2006.01.002HE Yu-qiang, MAO Bao-hua, CHEN Shao-kuan, et al. Research onthe methods of calculating the maximum assembling at railway passenger stations[J]. Journal of the China Railway Society, 2006, 28 (1): 6-11. (in Chinese) doi: 10.3321/j.issn:1001-8360.2006.01.002 [3] 张天伟. 铁路客运站旅客聚集规律研究[J]. 铁道学报, 2009, 31 (1): 31-34. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200901008.htmZHANG Tian-wei. Research on the assembling rule of passengers at railway passenger stations[J]. Journal of the China Railway Society, 2009, 31 (1): 31-34. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200901008.htm [4] 张天伟, 颜月霞, 王扬, 等. 铁路特大型客运站候车室面积和数量计算模型研究[J]. 铁道学报, 2010, 32 (2): 105-108. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201002020.htmZHANG Tian-wei, YAN Yue-xia, WANG Yang, et al. Research on the calculation models of area and number of waiting rooms at super-scale railway passenger stations[J]. Journal of the China Railway Society, 2010, 32 (2): 105-108. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201002020.htm [5] 汤波, 雷定猷, 张英贵, 等. 铁路车站咽喉通过能力计算方法[J]. 交通运输工程学报, 2010, 10 (6): 69-74. doi: 10.3969/j.issn.1671-1637.2010.06.012TANG Bo, LEI Ding-you, ZHANG Ying-gui, et al. Calculating method of carrying capacity for railway station bottleneck[J]. Journal of Traffic and Transportation Engineering, 2010, 10 (6): 69-74. (in Chinese) doi: 10.3969/j.issn.1671-1637.2010.06.012 [6] 史峰, 陈彦, 秦进, 等. 铁路客运站到发线运用和接发车进路排列方案综合优化[J]. 中国铁道科学, 2009, 30 (6): 108-113. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200906019.htmSHI Feng, CHEN Yan, QIN Jin, et al. Comprehensive optimization of arrival-departure track utilization and inboundoutbound route assignment in railway passenger station[J]. China Railway Science, 2009, 30 (6): 108-113. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK200906019.htm [7] NIE Lei, HUBi-song, FU Hui-ling, et al. Interaction analysis between night train operation and maintenance time on passenger dedicated railway line[J]. Journal of Transportation System Engineering and Information Technology, 2010, 10 (5): 66-72. doi: 10.1016/S1570-6672(09)60064-7 [8] LIEBCHEN C, SCHACHTEBECK M, SCHOBEL A, et al. Computing delay resistant railway timetables[J]. Computers and Operations Research, 2010, 37 (5): 857-868. doi: 10.1016/j.cor.2009.03.022 [9] DELORME X, GANDIBLEUX X, RODRIGUEZJ. Stability evaluation of a railway timetable at a station level[J]. European Journal of Operation Research, 2009, 195 (3): 780-790. [10] VANSTEENWEGEN P, VAN OUDHEUSDEN D. Developing railway timetable which guarantee a better service[J]. European Journal of Operation Research, 2006, 173 (1): 337-350. [11] GOVERDE R M P. Adelay propagation algorithm for largescale railway traffic networks[J]. Transportation Research Part C: Emerging Technologies, 2010, 18 (3): 269-287. [12] BURDETT R L, KOZAN E. A disjunctive graph model and framework for constructing new train schedules[J]. European Journal of Operation Research, 2010, 200 (1): 85-98. [13] BURDETT R L, KOZAN E. Techniques for inserting additional trains into existing timetable[J]. Transportation Research Part B: Methodological, 2009, 43 (8/9): 821-836. [14] CASTILLO E, GALLEGO I, URENA G J, et al. Timetabling optimization of a mixed double-and single-tracked railway network[J]. Applied Mathematical Modelling, 2011, 35 (2): 859-878. [15] CORMAN F, D'ARIANO A, PACCIARELLI D, et al. A tabu search algorithm for rerouting trains during rail operations[J]. Transportation Research Part B: Methodological, 2010, 44 (1): 175-192. -






 下载:
下载:



 下载:
下载: