0.   引言

跨座式单轨交通转弯半径小, 线路占地少, 爬坡能力强, 通过噪声小, 乘坐舒适, 视野开阔, 安全性好, 潜在地质灾害少, 造价低, 地形适应性强。这些特点决定其正成为山地城市、中小城市和海滨城市轨道交通首选型式之一^[1]。美国、日本和意大利等许多国家都修建了单轨系统, 其中日本建成线路最多。

但单轨车辆特殊结构造成了轮胎磨损严重, 突出表现在走行轮、导向轮和稳定轮构成的行驶系统虽然保障了运行不脱轨和小半径运行, 但又因其“超静定结构”造成轮胎磨损严重, 寿命低。据现场调查, 重庆市3号线走行轮和导向轮每10个月就需更换, 稳定轮每12个月需更换。按照3号线36列6辆车编组列车估算, 轮胎磨损造成的运营维护成本高达2 000~4 000万元。另外, 轮胎严重磨损还会造成轮胎附着能力大幅降低, 车辆驱动效率低, 制动距离长等问题, 严重影响车辆运行安全和运行节能。

目前, 国内外针对跨座式单轨车辆的研究主要围绕2个方向开展: 以轨道梁为研究对象, 将单轨车辆作为移动载荷, 分析移动载荷下轨道梁的动态响应特性。如Lee等分别进行的单轨车辆与轨道梁系统耦合动态响应分析^[2-4], 因主要研究轨道梁垂向动态响应特性, 因此, 研究中轨道梁模型较复杂, 对车辆动力学模型作了较大简化, 只考虑走行轮、导向轮与稳定轮垂向特性。以单轨车辆为主要研究对象, 通过多体动力学方法, 基于单轨车辆动力学模型, 对单轨车辆动力学性能进行仿真分析。如Goda等进行的单轨车辆动力学性能分析^[5-6], 建立的动力学模型考虑了轮胎垂向特性和侧偏特性, 由于主要关注车辆运行稳定性和舒适性, 为减小模型复杂度, 采用线性化轮胎模型建立单轨车辆动力学方程。

大量研究证实: 轮胎磨损量与轮胎与路面间作用的切向力密切相关, 车路系统动力学模型是研究轮胎磨损的基础。前期研究虽尚未涉及走行轮磨损的相关研究, 但前述学者建立的单轨车辆与轨道梁系统动力学模型可为本文研究提供坚实基础, 本文将参考国内外学者建立的单轨车辆动力学模型, 考虑走行轮、导向轮与稳定轮垂向特性、侧偏特性、纵向滑转特性与非线性刚度特性, 建立了适用于走行轮磨损分析的单轨车辆与轨道系统动力学模型, 针对单轨车辆曲线运行状态下, 从影响轮胎消耗的摩擦功的因素着手, 寻求降低轮胎磨损的最佳设计参数。

1.   轮胎磨损指标

1.1   轮胎磨损率

跨座式单轨车辆采用的是充氮气橡胶轮胎, 轮胎磨损机理异常复杂, 影响轮胎磨损的因素众多, 前期大量研究表明, 轮胎磨损大小取决于轮胎每转单位面积磨损率R^[7], 而轮胎磨损率与轮胎滚动过程中所消耗摩擦功E_F成正比

式中: γ为耐磨性系数。

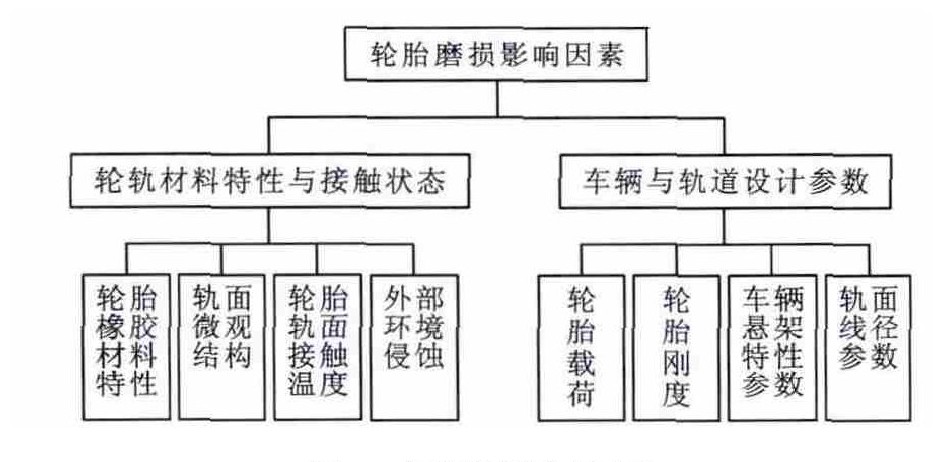
轮胎滚动过程中轮胎载荷、轮胎结构、车辆悬架特性、轮胎材料特性、路面结构、路面轮胎接触温度、雨雪、灰尘、泥土等与轮胎磨损量密切相关, 单轨轮胎磨损率影响因素见图 1。轮胎磨损量与影响因素间内在关系异常复杂, 但绝大多数复杂的影响因素都反映在耐磨系数上^[8]

图  1  轮胎磨损影响因素

Figure  1.  Influencing factors of tire wear

下载: 全尺寸图片 幻灯片

单轨车辆因内、外侧走行轮同轴支承, 在曲线行驶状态下, 轮胎磨损加剧, 本文从轮胎侧偏刚度对轮胎消耗摩擦功的影响着手, 固定轮胎载荷与轨面线径参数, 探讨在曲线行驶状态下, 单轨车辆轮胎性能参数对走行轮磨损率的影响。

1.2   轮胎摩擦功

轮胎磨损率与轮胎消耗摩擦功成正比, 轮胎摩擦功^[9]可定义为

式中: F_l为切向力; s为车辆行驶距离; dl为切向位移增量。

单轨车辆直线行驶时轮胎消耗的摩擦功为

式中: F_x为纵向力; dx为纵向(x向) 位移增量; s_x为纵向行驶距离。

车辆曲线运行时轮胎消耗摩擦功为

式中: F_y为横向力; dy为横向(y向) 位移增量; s_y为横向行驶距离。

路段轮胎消耗摩擦功为

如果车辆纵向速度为V_x, 横向速度为V_y, 纵向滑移率为ε, 则稳态条件(F_x、F_y不变) 下纵、横向轮胎消耗磨擦功依次为

式中: α为侧偏角; V为车辆行驶速度; T为行驶时间。

1.3   轮胎磨损量

轮胎磨损量与轮胎磨损率关系为^[10]

式中: W为轮胎磨损量; n为轮胎滚动转数; A为轮胎接地磨损面积。

车辆直线运行时轮胎磨损量为

式中: K_x为轮胎纵向刚度; F为法向力; F₀为参考法向力。

车辆曲线运行时轮胎磨损量为

式中: K_y为轮胎侧偏刚度。

由上述理论分析可知, 在曲线运行工况下, 当轮胎垂向载荷一定时, 横向力与侧偏刚度和侧偏角成正比, 轮胎磨损量与侧偏刚度和侧偏角平方成正比。但跨座式单轨车辆与轨道间接触形式独特, 走行轮除了与顶部轨面接触外, 导向轮与稳定轮在一定预压力作用下分别与两侧轨道黏着接触, 走行轮横向力和横向位移的大小除了与轮胎侧偏刚度有关外, 也受到两侧导向轮与稳定轮径向力的约束影响, 随着轮胎侧偏刚度的变化, 其横向力和横向滑移变化情况需深入研究。

2.   跨座式单轨车辆-轨面建模

2.1   单轨车辆结构拓扑关系

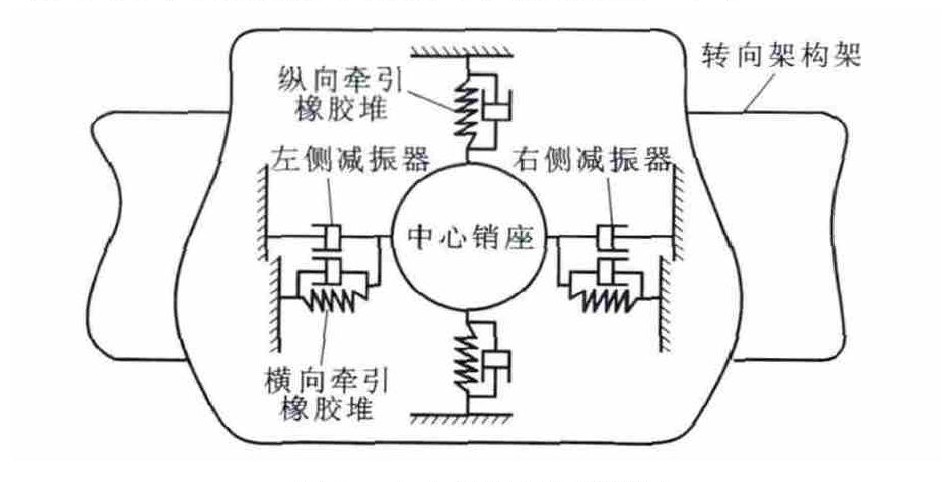
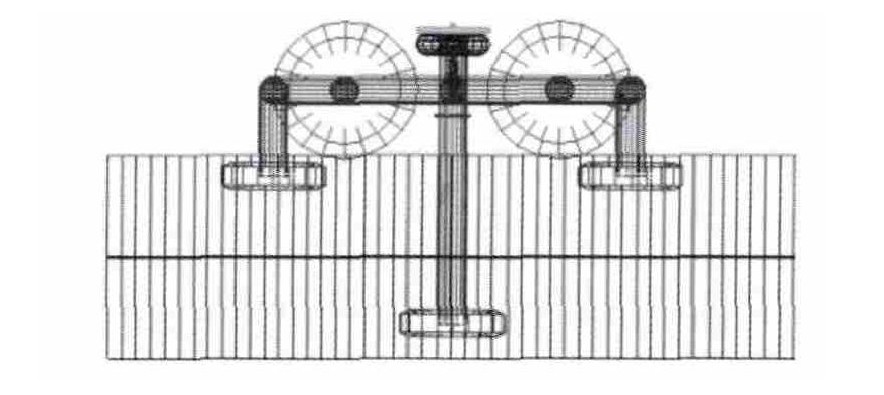
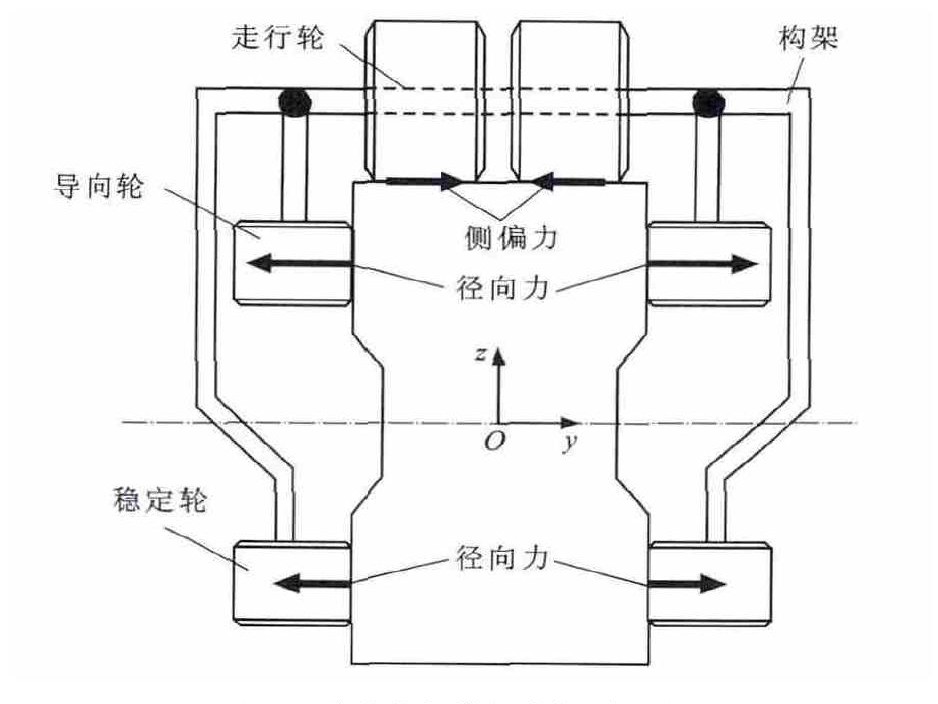
跨座式单轨车辆主要由4~6辆单车组成, 每辆单车由1个车体与前、后2个转向架组成。走行轮通过驱动轴刚性支撑, 与轨道梁顶部接触; 4个导向轮对称布置在转向架构架四角, 紧贴着轨道梁侧面滚动, 引导车辆沿轨道行驶; 2个稳定轮对称固定在构架中间两侧, 紧靠轨道梁侧面下部行驶, 起着稳定车辆运行状态的作用。单轨车辆结构特殊, 相比其他轨道车辆, 建模关键在于处理好单轨车辆中央悬挂装置建模及单轨车辆走行轮与顶部轨面和导向轮、稳定轮与侧部轨面三向轮轨附着接触建模。单轨车辆中央悬挂结构拓扑关系见图 2、3。

图  2  中央悬挂结构俯视图

Figure  2.  Top view of central suspension structure

下载: 全尺寸图片 幻灯片

图  3  中央悬挂结构正视

Figure  3.  Front view of central suspension structure

下载: 全尺寸图片 幻灯片

车体直接坐落在空气弹簧上。减振器45°斜装, 一端连接构架, 另一端连接中心销座。中心销上端固定在车体上, 下端与安装在转向架上的中心销座固连。

单轨车辆采用带橡胶堆的低横向刚度的空气弹簧来改善乘客的乘坐舒适性和提高车辆曲线通过性, 空气弹簧具有3个方向的刚度和阻尼, 采用轴套力模拟空气弹簧。

横向油压减振器以38°角安装在车体和转向架构架间, 在垂向、横向2个方向具有刚度和阻尼, 采用拉压弹簧阻尼力模拟。

为了防止运行过程中牵引力波动, 给牵引橡胶堆施加约为5kN预压力, 压缩到中心销座上, 而后固定于转向架构架上, 采用拉压弹簧阻尼力模拟其压缩性能。

横向止挡用于车辆通过轨道曲率很大且速度很高时防止车体滚摆角过大。当车辆直线行驶时, 横向止挡受力为0;当车辆进入弯道运行时, 由于离心力的作用, 内侧横向止挡不受力, 外侧横向止挡受力。2个横向止挡一端对称固定在转向架构架顶端中心面中心销的两侧, 另一端与中心销有10mm间隙。采用单边冲击力模拟横向止挡。单轨车辆动力学模型主要参数见表 1。

表  1  单轨动力学模型主要参数

Table  1.  Main parameters of monorail dynamics model

下载: 导出CSV 

| 显示表格

2.2   轮轨接触建模

跨座式单轨车辆与轨道间接触形式独特, 走行轮与顶部轨面黏着接触, 见图 4, 导向轮与稳定轮在一定预压力作用下分别与两轨道侧面黏着接触, 整个结构走行轮、导向轮与稳定轮与“3个方向轨面”黏着接触。

图  4  走行轮与顶部轨面接触

Figure  4.  Running wheel in contact with the top surface of track beam

下载: 全尺寸图片 幻灯片

走行轮与顶部轨面相互作用力^[11]为

式中: m₁为车身集中质量; m₂为转向架集中质量; g为重力加速度; l_x1为车身质心到前空气弹簧距离; l_x为前、后空气弹簧距离; k_z为走行轮垂向刚度; S为转向架质心垂向相对位移; c_z为走行轮垂向(z向) 阻尼; F_ry、F_rx、F_rz分别为走行轮与轨面间横向力、纵向力与垂向力; k_y为走行轮横向刚度; k_x为走行轮纵向刚度; θ_y为转向架点头角; θ_x为转向架侧倾角; H_z为轮轨接触处路面输入位移; l_x2为走行轮与转向架质心纵向距离; Z为转向架垂向位移; j=1时为前轮, j=2时为后轮。

按式(11) ~ (13) 轮轨接触建模要求, 建立能反映轮胎与轨面接触情况的轮胎模型和路面模型, 轮胎模型采用纯解析轮胎模型^[12]; 对于轨道面模型, 建立沿单轨车辆实际运行线路中心线, 以中心线为基准沿其法向拉伸成精度较高的四边形单元, 以此方法建立轨道梁顶部、两侧部共3个轨面, 3个轨面分别与走行轮、导向轮、稳定轮接触^[13], 见图 5、6。

图  5  走行轮、导向轮、稳定轮与侧部轨面接触

Figure  5.  Running wheels, steering wheels and stabilizing wheels in contact with side surface of track beam

下载: 全尺寸图片 幻灯片

图  6  走行轮与轨道梁顶部接触

Figure  6.  Running wheels in contact with top of track beam

下载: 全尺寸图片 幻灯片

2.3   轨道线路建模

考虑线路上缓和曲线、纵向坡度、曲线超高、轨道间接缝、进站时道岔结构特征等因素, 建立由直线段、曲线段、缓和曲线段组合而成的能反映实际轨道特征的典型轨道模型^[2]。轨道模型由3段组成: 前一段为100m直线段, 连接半径为100m、曲线起止夹角为60°、超高为40.8 mm的曲线段, 之后又是100m直线段, 见表 2。

表  2  轨道模型参数

Table  2.  Parameters of track beam model

下载: 导出CSV 

| 显示表格

2.4   导向轮与稳定轮预压力模拟

设置导向轮和稳定轮预压力为4.9kN, 在建模中, 将导向轮和稳定轮与路面接触面处相对路面每侧嵌入5mm, 模拟预压力^[14]。

3.   仿真结果分析

因轮胎磨损量与轮胎滚动所消耗的摩擦功成正比, 摩擦消耗功又正比于车辆曲线行驶时轮胎所受的横向力, 因此, 观察车辆运行过程中, 走行轮所受侧偏力与相应的侧偏角。

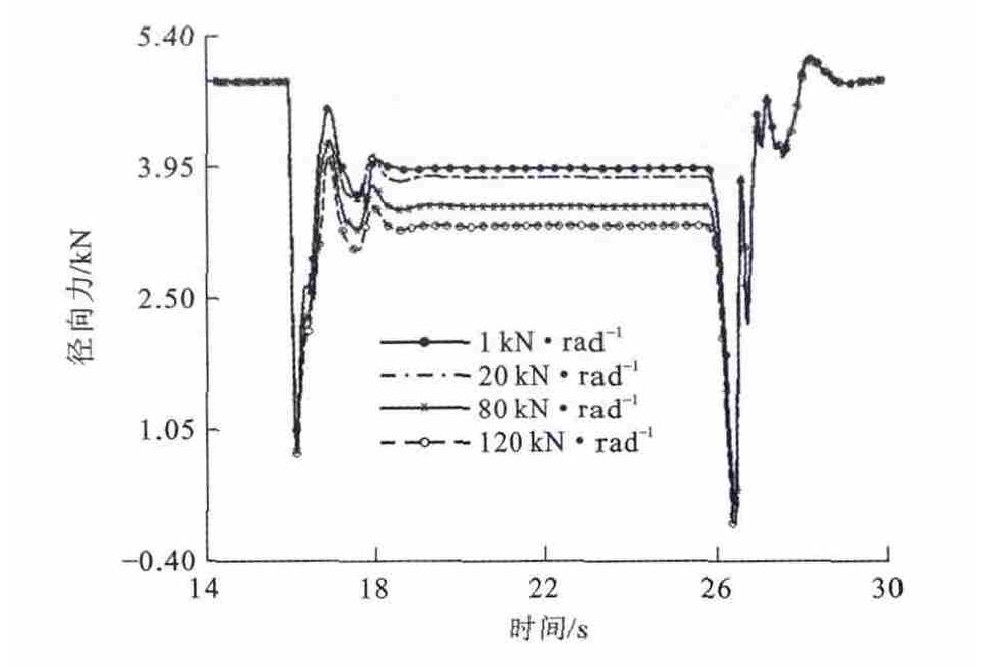
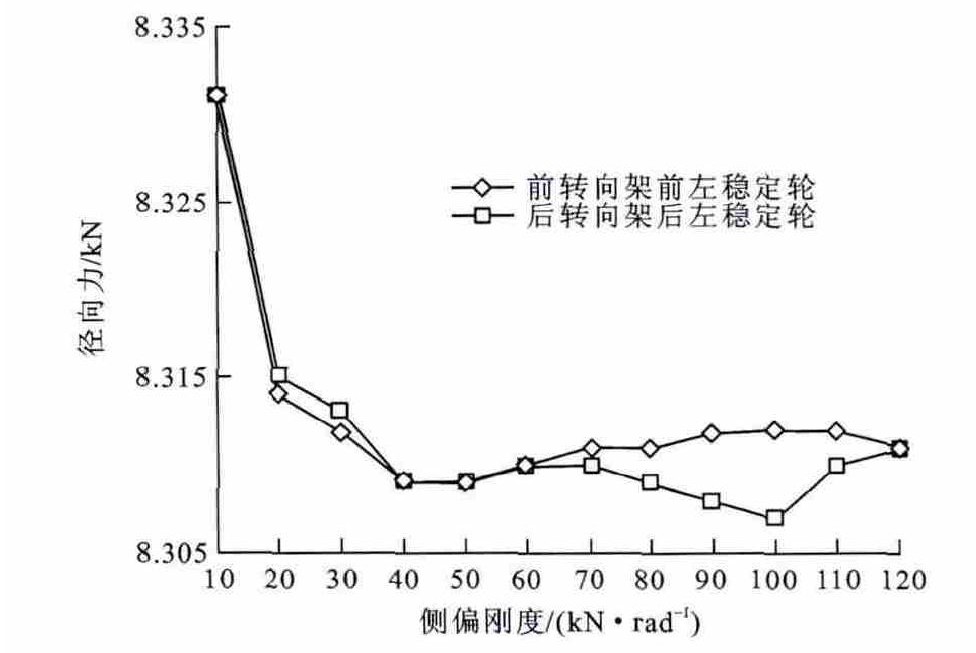
设定运行工况为: 从0时刻起步, 2s内加速至36km·h^-1, 保持该速度匀速行驶至终点。参考原始设计参数, 设定垂向刚度为1 180kN·m^-1, 走行轮初始侧偏刚度为1kN·rad^-1, 将侧偏刚度从1kN·rad^-1以1 kN · rad^-1的增量递增到120kN·rad^-1, 仿真得到单轨车辆轮轨接触处导向轮和稳定轮径向力与走行轮侧偏力。因数据较多, 抽取侧偏刚度为1、20、80、120kN·rad^-1, 前转向架前左导向轮径向力仿真结果对比见图 7, 前转向架前右导向轮径向力对比见图 8, 前转向架左、右稳定轮径向力对比见图 9, 前转向架前左、后右走行轮侧偏力对比见图 10。可以看出, 单轨车辆直线行驶时, 导向轮和稳定轮的径向力均为4.9kN, 这与导向轮与稳定轮的实际预压力相等; 车辆进入曲线段后, 导向轮与稳定轮径向力发生变化, 随着走行轮侧偏刚度增加, 前转向架左侧导向轮的径向力稳态值增加, 前转向架右侧导向轮径向力稳态值下降; 走行轮侧偏刚度的变化对左、右稳定轮径向力稳态值影响很小; 在直线段时走行轮侧偏力为0, 进入曲线段后, 随着走行轮侧偏刚度的增加, 前转向架前左和后右走行轮侧偏力稳态值朝相反的方向逐渐增加。

图  7  前转向架左侧导向轮径向力曲线

Figure  7.  Radial force curves of left steering wheel

下载: 全尺寸图片 幻灯片

图  8  前转向架前右导向轮径向力曲线

Figure  8.  Radial force curves of front-right steering wheel of front bogie

下载: 全尺寸图片 幻灯片

图  9  前转向架左、右稳定轮径向力曲线

Figure  9.  Radial force curves of left and right stabilizing wheels of front bogie

下载: 全尺寸图片 幻灯片

图  10  前转向架前左、后右走行轮侧偏力曲线

Figure  10.  Cornering force curves of front-left and rear-right running wheels of front bogie

下载: 全尺寸图片 幻灯片

为完整分析走行轮侧偏刚度对轮胎磨损的影响趋势, 将单轨车辆在曲线段行驶时, 各导向轮、稳定轮径向力稳态值与走行轮侧偏力和侧偏角稳态值随走行轮侧偏刚度变化绘制成曲线, 为看清其趋势变化, 将转向架右侧导向轮径向力值统一乘以负号, 见图 11~14。从图 11、12可以看出, 当走行轮侧偏刚度在10~120kN·rad^-1间变化时, 单节车辆前、后转向架的前左、后右导向轮径向力逐渐增大, 前右、后左导向轮径向力逐渐减小, 但变化很小。从图 13可以看出, 当走行轮侧偏刚度在10~20kN·rad^-1间变化时, 前转向架前左、前右走行轮侧偏力逐渐增大, 后左、后右走行轮侧偏力则逐渐减小, 但其值都较小, 故走行轮磨损较小, 此时, 走行轮侧偏力方向相同, 说明转向架上的走行轮往同一个方向侧滑。当走行轮侧偏刚度在20~120kN·rad^-1间变化时, 随着侧偏刚度增大, 前、后走行轮侧偏力同时朝相反方向增大。从图 14可知, 随着走行轮侧偏刚度增大, 走行轮侧偏角也呈现微量变化。但经计算, 如果走行轮侧偏刚度超过120kN·rad^-1, 其侧偏角将急剧增大, 进入非线性区域。

图  11  单节车辆8个导向轮径向力曲线

Figure  11.  Radial force curves of eight guide wheels of a vehicle

下载: 全尺寸图片 幻灯片

图  12  前、后转向架左侧稳定轮径向力曲线

Figure  12.  Radial force curves of left stabilizing wheels of front and rear bogies

下载: 全尺寸图片 幻灯片

图  13  走行轮侧偏力与侧偏刚度关系曲线

Figure  13.  Relationship curves of cornering forces and cornering stiffnesses of running wheels

下载: 全尺寸图片 幻灯片

图  14  走行轮侧滑角与侧偏刚度关系曲线

Figure  14.  Relationship curves of side slip angles and cornering stiffnesses of running wheels

下载: 全尺寸图片 幻灯片

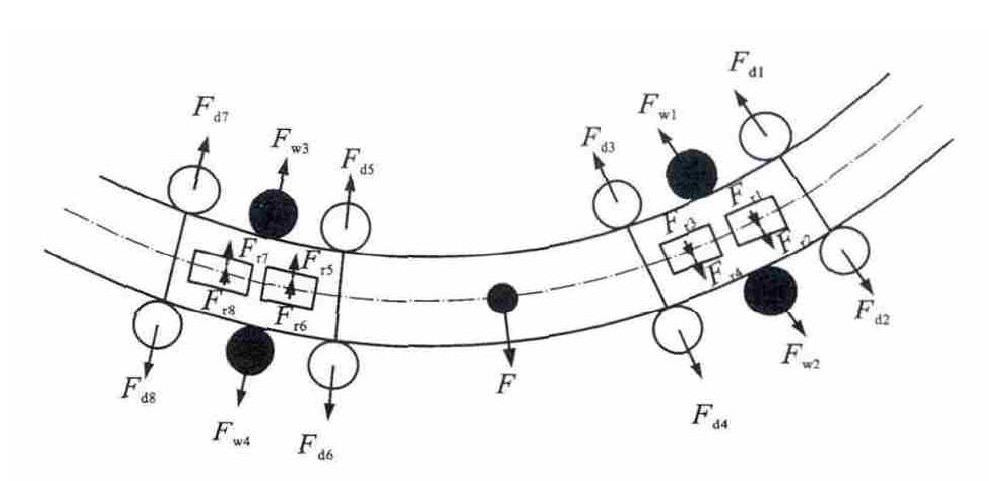
由于跨座式单轨车辆与轨道间接触形式独特, 走行轮、导向轮与稳定轮与“3个方向轨面”均发生接触。单轨车辆曲线行驶时, 其走行轮与顶部轨面间的侧向力将受到导向轮、稳定轮和轨面间径向力大小的影响, 其受力分析见图 15、16。车辆质心侧向力F_y为

图  15  单节车辆横向受力俯视图

Figure  15.  Top view of lateral forces of single vehicle

下载: 全尺寸图片 幻灯片

图  16  单节车辆横向受力后视图

Figure  16.  Rear view of lateral forces of single vehicle

下载: 全尺寸图片 幻灯片

式中: F_d1y~F_d8y分别为前、后转向架导向轮所受径向力F_d1~F_d8在y向的分力; F_w1y~F_w4y分别为前、后转向架稳定轮所受径向力F_w1~F_w4在y向的分力; F_r1y~F_r8y分别为前、后转向架走行轮所受侧偏力F_r1~F_r8在y向的分力; F_c为因轨面超高产生的重力分力。

从图 15与式(14) 可清晰看出, 在单轨车辆速度与轨道半径一定的情况下, 导向轮、稳定轮与轨面间径向力将直接影响走行轮侧偏力的大小与方向, 单轨车辆走行轮侧偏刚度的变化, 引起了导向轮、稳定轮与轨面间径向力变化。通过分析发现: 曲线行驶时走行轮侧偏角变化较小, 侧偏力随着走行轮侧偏刚度的增加而增大, 结合曲线工况下轮胎磨损指标, 可知随着单轨走行轮侧偏刚度增大, 单轨列车在曲线行驶时磨损量将加大。

从单轨走行轮磨损角度分析, 走行轮侧偏刚度越小越好, 但走行轮侧偏刚度过小, 由于走行轮侧偏力方向相同, 不足以形成曲线通过时所需的摇头力矩, 车辆曲线通过性将受到影响。走行轮侧偏刚度继续增大到20kN·rad^-1时, 左、右侧走行轮侧偏力方向开始相反, 说明走行轮侧偏力开始形成摇头力矩, 车辆的曲线通过性开始好转。走行轮侧偏刚度从20kN·rad^-1增大到120kN·rad^-1的过程中, 左、右侧走行轮侧偏力同时朝相反的方向一直增大, 这就意味着走行轮侧偏力所形成的的摇头力矩也一直增大, 因车辆曲线通过时具有一个最佳导向力矩, 该力矩增大到形成的摇头力矩达到最佳时(3.98kN·m), 就不宜再增大。走行轮侧偏力增大到一定程度后, 不仅磨损严重, 而且有可能使得轮胎侧偏角超出轮胎侧偏特性的线性范围。由此, 随着走行轮侧偏刚度的增大, 不管是前轴上的左、右走行轮, 还是后轴上的左、右走行轮, 其横向力都呈现增大趋势。而随着侧偏刚度的增大, 其侧偏角变化并不大。

4.   结语

(1) 本文分析了单轨车辆在曲线行驶时, 随着走行轮侧偏刚度增加, 作用在走行轮上的侧偏力和侧偏角与导向轮和稳定轮的径向力的变化规律。

(2) 根据各参量随走行轮侧偏刚度的变化曲线, 剖析了走行轮侧偏力随侧偏刚度变化规律, 得出随着走行轮侧偏刚度增加, 受导向轮、稳定轮与其侧部轨面接触的径向力影响, 单轨车辆走行轮侧偏力逐渐增大, 走行轮侧偏角呈现微量变化。结合轮胎磨损指标, 得出随着走行轮侧偏刚度增加, 单轨车辆曲线行驶时轮胎磨损量以1.2%的速率增加。

(3) 走行轮侧偏刚度大小除了影响车辆曲线行驶的轮胎磨损外, 对车辆曲线通过性也有影响, 过小的走行轮侧偏刚度将不足以形成曲线通过时所需的摇头力矩, 因此, 为减小单轨车辆在曲线行驶时轮胎磨损, 在满足单轨车辆最佳通过性能下(摇头力矩为3.98kN·m), 单轨车辆走行轮侧偏刚度设计值推荐为9.37kN·rad^-1。