Improved draft survey method based on densified table of offsets
-
摘要: 为了提高水尺计重的精度, 提出一种不依赖于船舶装载手册的改进水尺计重方法。基于加密型值表建立船舶高精度数据库, 并计算船舶排水量。根据六面吃水数据计算船舶浮态参数与中垂(拱) 量。根据材料力学中梁的弯曲理论, 用圆弧拟合船舶拱垂变形曲线, 计算出船舶每一站的中垂(拱) 量, 通过对型值坐标点进行坐标修正, 得到船舶中垂(拱) 状态下的数据库。根据浮态参数, 通过坐标系变换、S-H剪裁算法计算船舶自由浮态下的排水量。以某散货船为例, 分别计算了船舶正浮、纵倾与中拱状态下的排水量, 并与传统水尺计重方法进行了比较分析。计算结果表明: 正浮时改进水尺计重方法相对误差较小, 平均为0.085 6%, 纵倾时平均相对误差增大到0.414 5%, 中拱状态下平均相对误差增大为0.619 9%。改进的水尺计重方法提高了计算精度, 且适用于船舶自由浮态, 具有一定的工程应用价值。Abstract: In order to improve the accuracy of draft survey, an improved draft survey method that did not depend on ship loading manual was developed.The displacement of ship was calculated by using high-precision ship database that was established based on the densified table of offsets.The floating state parameters and sagging (hogging) value of ship were calculated according to six draft readings.In order to calculate the sagging (hogging) value of each station, the deformation curve of ship was fitted by circular arc according to the beam bending theory in material mechanics.The ship database in sagging (hogging) condition was constructed by the correction of offsets coordinate point.The displacement of ship in free floatation was calculated by using floating state parameters, coordinate system transformation and S-H polygon clipping algorithm.Taking a bulk carrier as an example, the displacements of ship in even keel, trim and hogging condition were calculated respectively, and compared with the calculation result of traditional draft survey method.Calculation result indicates that in even keel condition, the average relative error of improved draft survey method is smaller, about 0.085 6%, the average relative errors increase to 0.414 5% and 0.619 9% in trim and hogging condition respectively.The calculation accuracy of improved draft survey method increases, the method can be applied tofree floatation of ship, and has a certain engineering application value.
-
0. 引言
水尺计重[1]是通过测定承运船舶的排水量与船用物料, 依据船舶的标准图表计算出船舶载货质量的鉴定方式, 通过检测承运船舶的吃水, 求得船体相应的排水量。由于水尺计重速度快、成本低, 被广泛应用于散货船货物运输中。但水尺计重也存在一定缺陷, 船舶在横倾、纵倾与拱垂情况下误差会增大。
许多学者在减少计重误差方面进行了大量研究: 林火平分析了船舶常数对水尺计重的影响, 得出缆绳的松紧与压载水的测量是影响船舶常数的主要因素[2], 但研究仅局限于船舶常数对水尺计重误差的影响; 王淑敏等分析了压载水、油舱、燃油舱、污水舱等货舱的测量误差, 提出了几种正确测量其数值的可行方法[3], 但研究仅讨论了船舶正浮态情况, 并未对船舶在自由浮态下的情况进行讨论; 陈建锋分析了影响压载水准确测算的因素, 提出了几种可行的测量方法[4], 但方法均围绕压载水进行讨论; 李清林研究了水尺计重中吃水差和船舶长度之间的适用关系, 指出水尺计重过程中船舶吃水差和船舶长度的使用要相互对应[5], 但研究并未从根本上减少误差; 黄昱洪提出在极大纵倾情况下根本氏二次校正公式已不适用, 用船舶庞勒曲线计算船舶大纵倾下的排水量, 提高了计算精度[6], 但研究未讨论船舶处于拱垂状态下的情况, 且庞勒曲线在量取时也会因为人为因素产生误差; 刘辉强归纳并总结了可能导致水尺计重误差的诸多因素, 分析了其导致水尺计重误差的原因, 并简单介绍了水尺计重出现误差的后果和影响, 提出用微倾迭代的方法来处理船舶纵倾的情况[7], 但由于研究基于普通二维型值表, 也会产生较大的计算误差; Ran等基于图像处理来提高六面吃水数据测量精度, 减少了读数误差[8]; Gu等设计了一套数字测量系统, 通过对摄像机拍摄的照片进行图像处理来减少人为观察误差[9], 其本质也是减少读数误差; Ziha提出一种船舶外壳变形时的排水量计算方法[10], 相比传统加权平均法提高了计算精度; Ivce等分析了水尺计重过程中误差产生的原因, 提出用光纤技术来代替人工读数以达到减少误差的目的[11], 其本质上也仅仅减少了读数误差。
以上研究中减少水尺计重误差的举措均依赖于船舶设计部门提供的装载手册, 计重时要求船舶尽量减少横倾与纵倾, 并不能从根本上减少误差, 且对于拱垂的修正过于简化。本文提出了一种改进的水尺计重方法, 基于加密型值表建立船舶数据库, 直接计算排水量, 适用于船舶自由浮态, 相比传统的水尺计重方法, 提高了水尺计重的精度。
1. 传统水尺计重方法
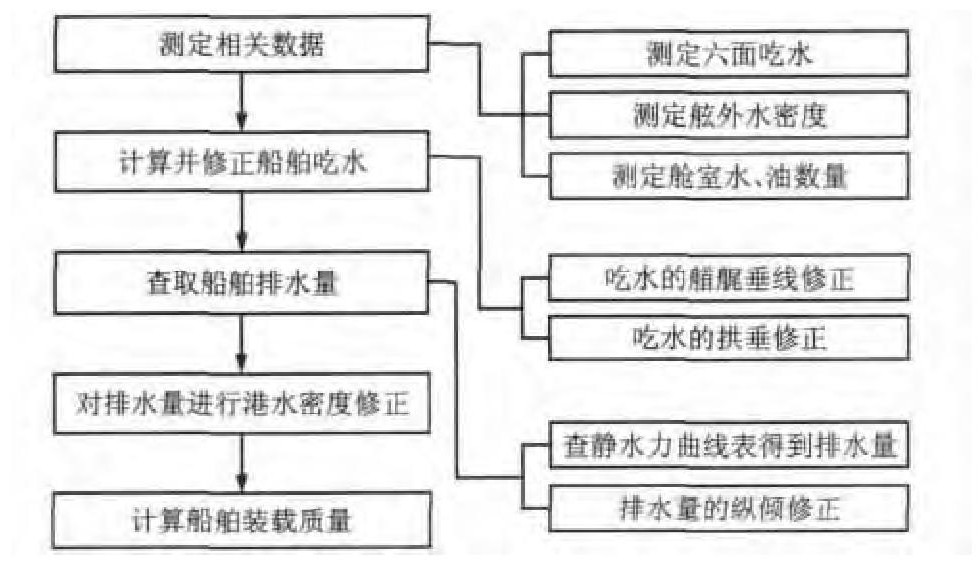
传统水尺计重方法流程见图 1。根据测得的六面吃水读数, 包括船艏、船舯与船艉两舷的水尺读数, 进行艏艉垂线修正与拱垂修正, 得到船舶平均吃水, 然后根据平均吃水查静水力曲线表得到排水量, 再在此基础上进行排水量的纵倾修正与港水密度修正, 计算出船舶装载质量。
2. 改进水尺计重方法
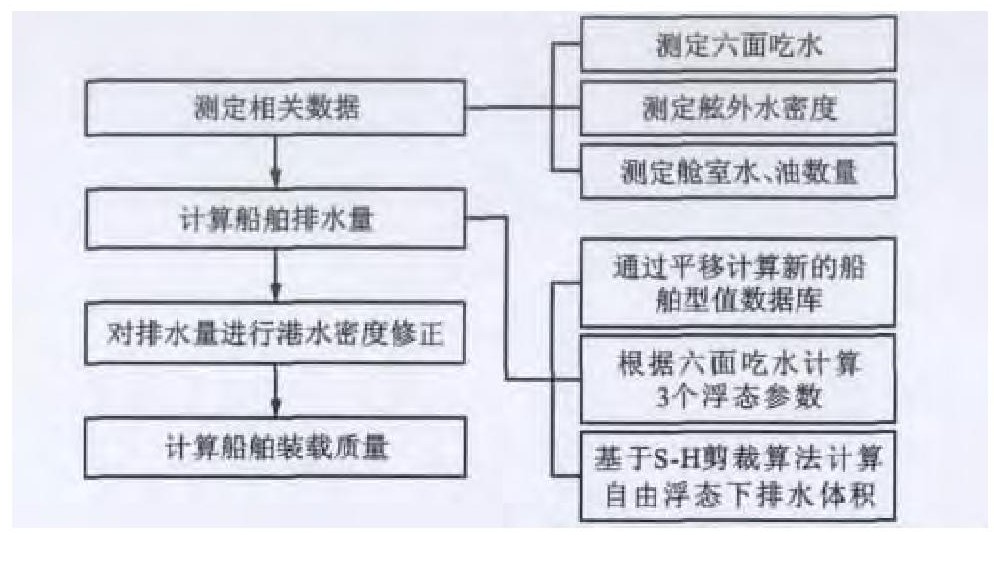
图 2为改进的水尺计重方法流程。改进的水尺计重方法不再依赖于装载手册, 而是基于加密型值表建立船舶高精度的三维数据库。并通过测得的六面吃水数据计算出船舶的浮态参数, 根据梁的弯曲理论将船舶的拱垂变形量化, 得到船舶变形后的精确数据库, 通过船舶横剖面和水线面求交, 计算出船舶的排水量。
2.1 基于加密型值表的船舶三维数据库的建立
加密型值表是指对普通型值表进行分站数目的加密而得到的型值表, 能更精确反映船体资料, 是船舶的真实外形数据[12-13]。国际上主流的船舶设计软件如NAPA等均可输出船舶的加密型值表。目前, 中国对加密程度还没有相应的标准, 主要根据实际需要进行合理的细分。以47 500t散货船舶太行128的加密型值数据为例, 船舶宽度和高度方向均以20mm为单位细分, 船长方向以0.04站(384mm) 为单位细分, 共包含958 099个型值点的三维坐标信息。
2.1.1 数据库的建立
编写VC++程序, 完成加密型值表的自动识别和读取, 建立了船舶高精度的三维数据库。由于加密型值表数据量大, 需要一种可行的方法来验证数据库的完整性。本文基于OpenGL语言实现船舶数据可视化来验证数据库的完整性。为了便于显示, 加大了数据显示间隔。图 3为太行128水线, 垂向间隔为1m。图 4为太行128横剖线, 纵向间隔为1m。
2.1.2 数据库的准确性验证
通过三维可视化方法验证数据库的完整性, 但是其准确性不能单从视觉上判断。本文编写程序计算了散货船舶太行128在正浮状态下不同吃水时的船舶各项静水力参数, 包括浮态参数和船型系数等, 并与装载手册中给出的数据进行比对, 计算误差对比结果见表 1, 具体计算方法参考文献[14-15]。
表 1 计算误差对比Table 1. Comparison of calculation errors
从表 1中数据可看出, 计算数据和装载手册中的数据基本吻合, 除浮心垂向坐标和每厘米吃水吨数外, 其余各项静水力参数和船舶装载手册中提供数据的误差精度都在0.01%左右, 甚至更小。浮心垂向坐标和每厘米吃水吨数的误差在0.1%这个量级, 误差仍然很小, 浮心垂向坐标误差约为0.001m, 每厘米吃水吨数的误差约为0.05t·cm-1。对比结果验证了船舶数据库的准确性, 可用于水尺计重计算。
2.2 船舶自由浮态下排水量的计算
2.2.1 坐标系、浮态参数与坐标变换矩阵
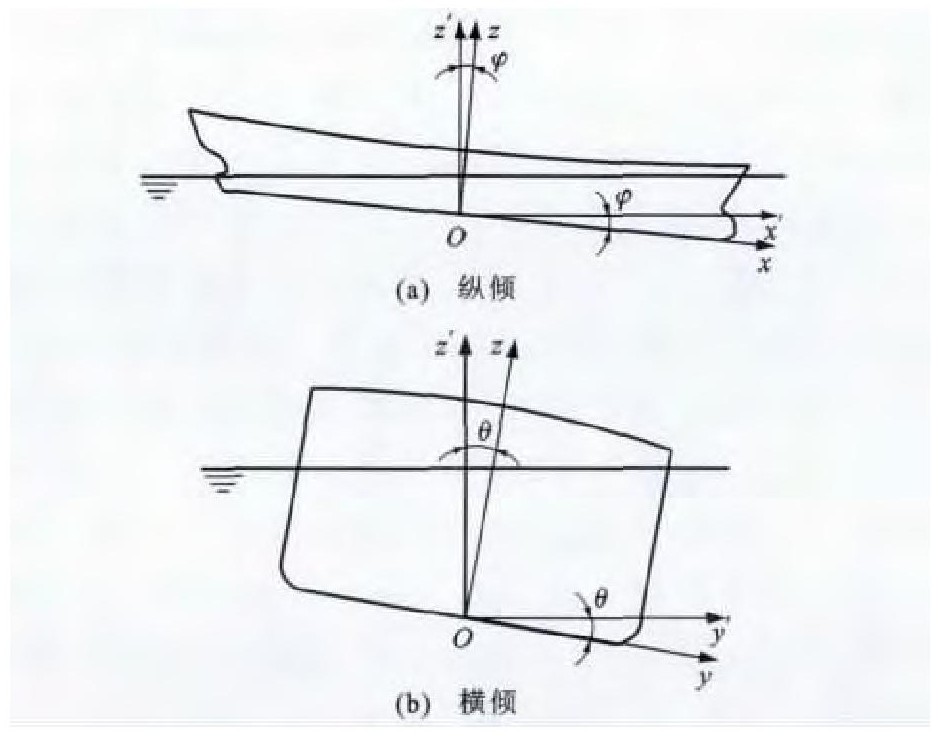
为研究船舶浮态问题, 采用2个左手坐标系[16-17], 见图 5, 静止海面固定坐标系为Ox′y′z′, 船体坐标系为Oxyz, 2个坐标系的原点重合, 原点选在船舶基平面、中横剖面和中纵剖面的交点上。规定x轴指向船艏为正, y轴指向右舷为正, z轴向上为正。浮态参数选择符拉索夫参数[8], 包括船舯吃水、横倾角θ、纵倾角φ, 并且规定向右舷和向船艏倾斜为正。根据文献[8], 可得到2个坐标系之间的变换矩阵。从船体坐标系Oxyz到固定坐标系Ox′y′z′的坐标变换矩阵B1为

式中: α为倾斜角, 即倾斜水线面与基准面的夹角。
从固定坐标系Ox′y′z′到船体坐标系Oxyz的坐标变换矩阵B2为

2.2.2 浮态参数的计算
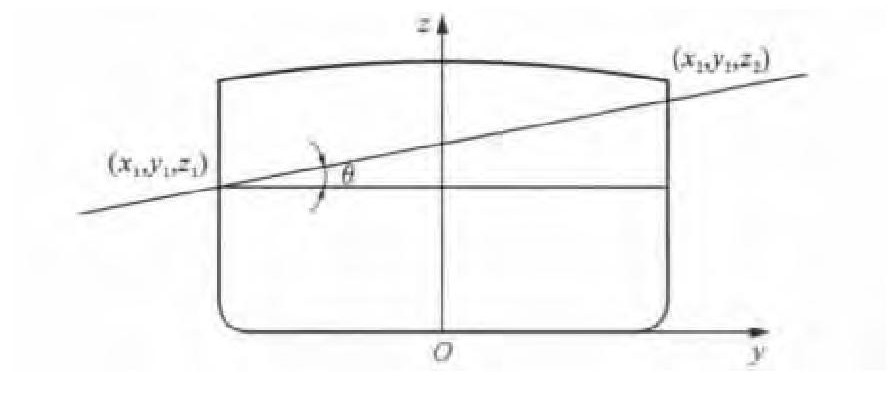
图 6为横倾角的计算原理, (x1, y1, z1) 和(x2, y2, z2) 分别为船舶左、右舷水尺读数型值坐标, 横倾角θ的计算式为

式中: d1、d2分别为船舯左舷与右舷吃水; B为船舶宽度。
同理得到纵倾角φ的计算式为

式中: d3、d4分别为船艏和船艉平均吃水; L为船舶垂线间长, 可由船舶完工图纸查得。
2.2.3 船舶拱垂修正
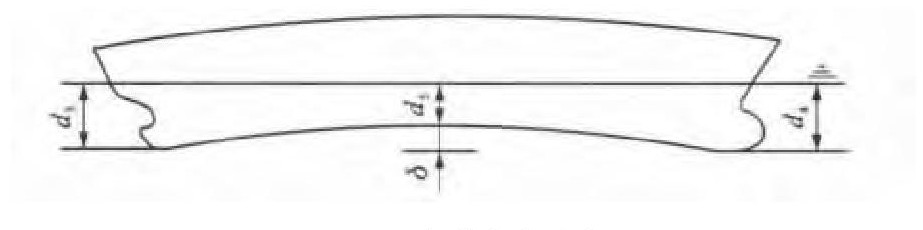
在船舶实际营运过程中, 由于装载情况的不同, 船体纵向会发生弯曲和变形, 即船舶的中拱(垂)。按照传统方法拱垂修正后总平均吃水dM为

式中: d5为船舯平均吃水。
采用加权求平均法减少了计重误差, 但不能从根本上减少误差。本文以船舶中拱状态为例, 探讨了一种更加精确的拱垂修正计算方法。图 7为固定坐标系下船舶中拱状态, δ为船舶拱垂值。
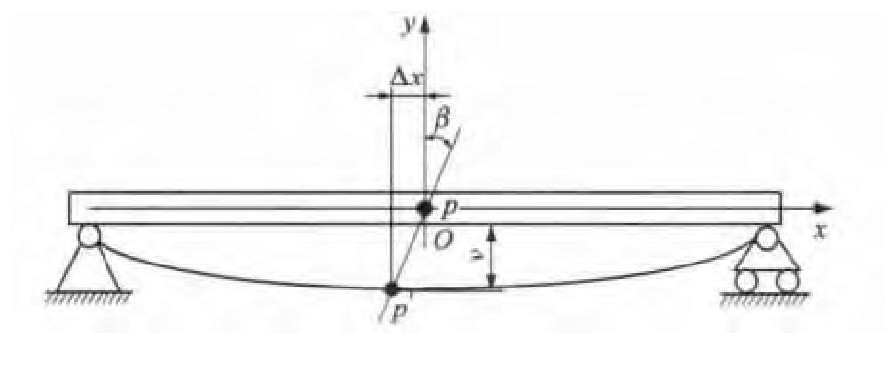
在进行弯曲变形计算时, 船体可近似视为空心的等截面梁。在材料力学中, 根据梁的弯曲理论, 描述梁变形的2个基本位移量为挠度v和转角β。图 8为梁弯曲理论, 其中: p为梁的中心点; p′为p弯曲后的位置; 挠度v为横截面形心沿垂直于轴线方向的线位移, v向下为正, 反之为负; 转角β为横截面绕其中性轴转动的角度, 顺时针转动为正, 反之为负; Δx为横截面形心沿轴线方向的线位移, 在小变形情况下, Δx很小, 通常可以忽略不计。
据统计, 船舶正常的拱垂值为L/1 200, 极限的拱垂值为L/800, 危险的拱垂值为L/600, 因此, 船舶的拱垂变形为小变形。小变形时, 梁的任一截面的转角等于挠曲线对应点的切线。在纯弯曲时, 曲率为常数, 挠曲线为一段圆弧。
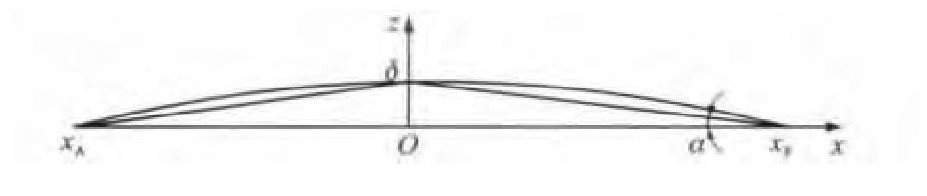
挠曲线转角的计算见图 9, 其中: xA为船艉纵向坐标; xF为船艏纵向坐标。根据三角关系, 可得

则α不大于0.095°。由于α很小, 曲线上各点的切线斜率接近于0, 故转角β可忽略不计, 只计算船舶在竖直方向上的形变量。
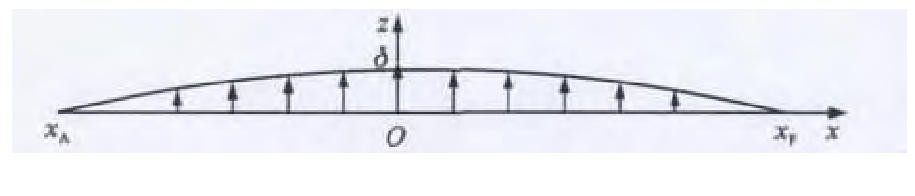
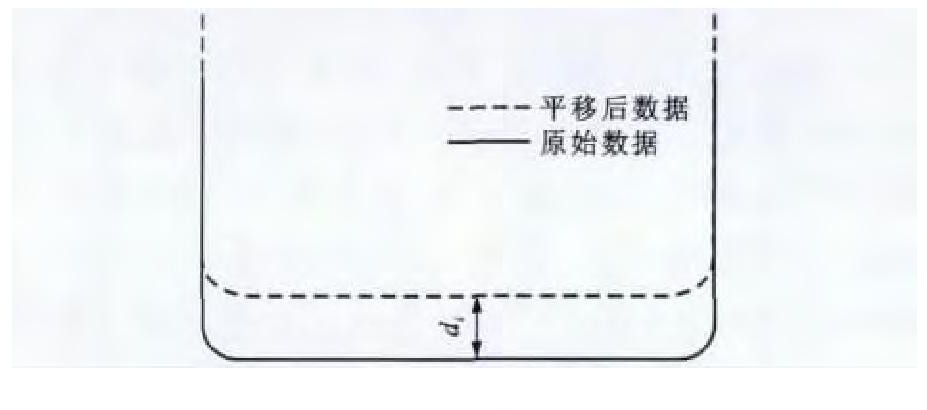
船舶中拱时, 船舶在船体坐标系下的型值坐标将发生改变。从船艏到船艉型值坐标数据在原始数据的基础上整体垂向平移, 各个型值坐标平移量di不同, i为船舶站号, 见图 10, 某横剖面型值点平移前后的对比见图 11。
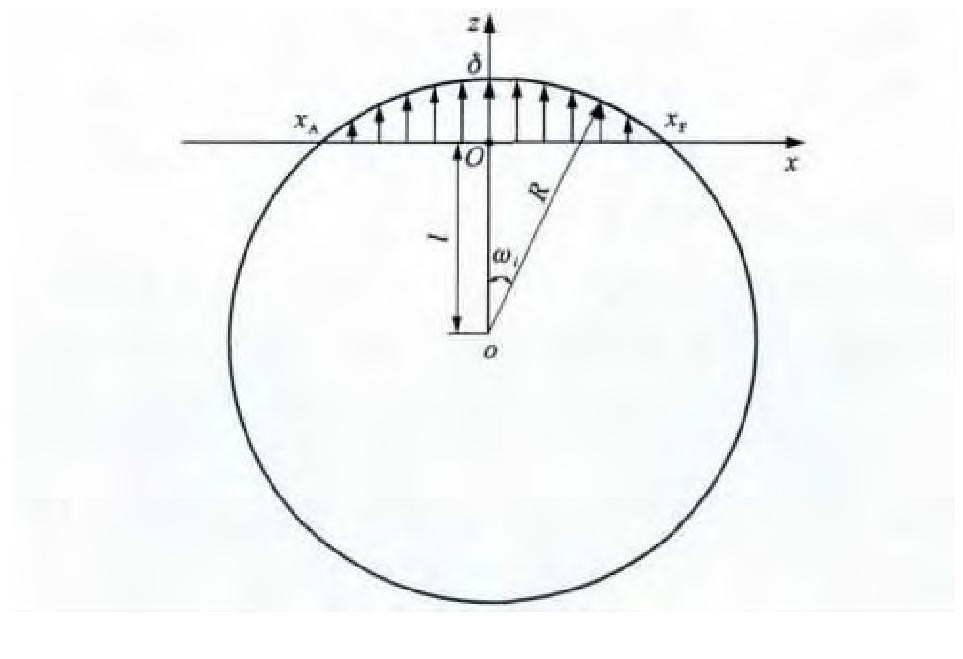
在计算各站的平移量时, 拱垂变形曲线为一段圆弧, 见图 12。在船体坐标系下, 其参数方程为

式中: wi为船舶站号为i的型值点与圆心的连线与垂直方向的夹角; R为拟合圆弧半径; l为圆心o到船体坐标系原点O的距离。
船舶各站横剖面到船舯的距离s已知

式中: xi为船舶站号为i的型值纵向坐标; xM为船舯纵向坐标。
联立式(9) 可得各站型值的平移量为

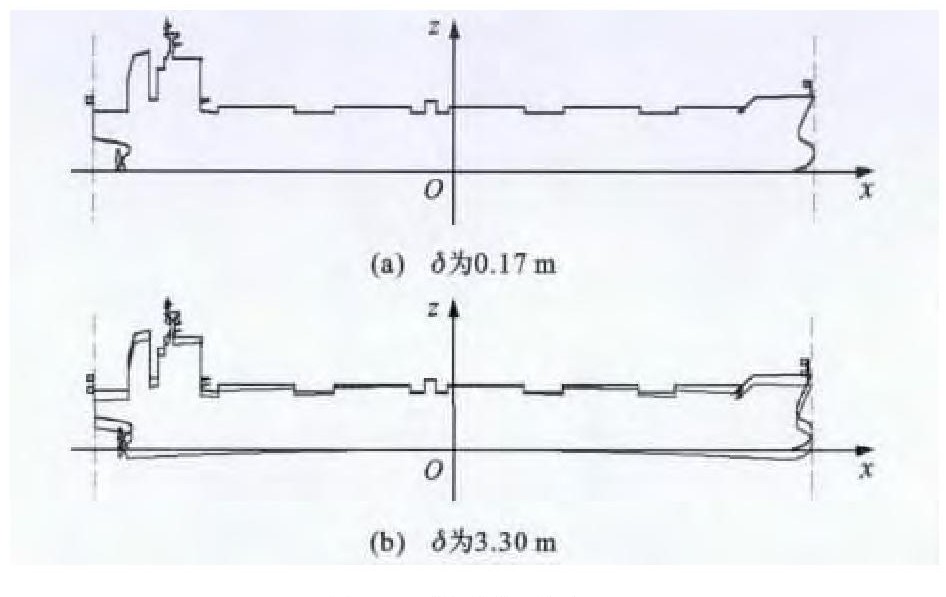
编写VC++程序对拱垂变形进行验证, 图 13为中纵剖面二维效果, 图 13 (a)取正常拱垂值δ为0.17m, 其圆弧线基本为一条直线。为了便于验证, 假设船舶拱垂值δ为3.30m, 见图 13 (b)。图 14为拱垂变形后的三维效果, 拱垂值δ为3.30m。
计算出船舶中拱(垂) 后的型值数据库以后, 问题就转换为求船舶自由浮态下的排水量。
2.2.4 基于S-H算法求排水量
在固定坐标系下, 水线面是固定不变的。求取排水量的思路如下: 建立好的船舶数据库通过坐标系变换, 转换到固定坐标系下, 计算每一站横剖面和水线面的交点情况, 然后转换到船体坐标系下, 计算出水线面下每一站横剖面的面积, 纵向积分求出水下排水量。
应用多边形剪裁Sutherland-Hodgman算法(简称S-H剪裁算法)[18-19], 确定船舶自由浮态下横剖面与水线面的交点情况, 算法无需进行任何分类, 且速度快, 精确度高, 易于代码实现, 通用性好。
S-H剪裁算法的总体策略是顺序地将每一多边形的一对顶点送给一组裁剪器(左、右、下、上), 一组裁剪器完成对一对顶点的处理后, 将该边留下的坐标值立即送给下一组裁剪器, 最终输出的为一个完整的多边形填充区边界的顶点队列。
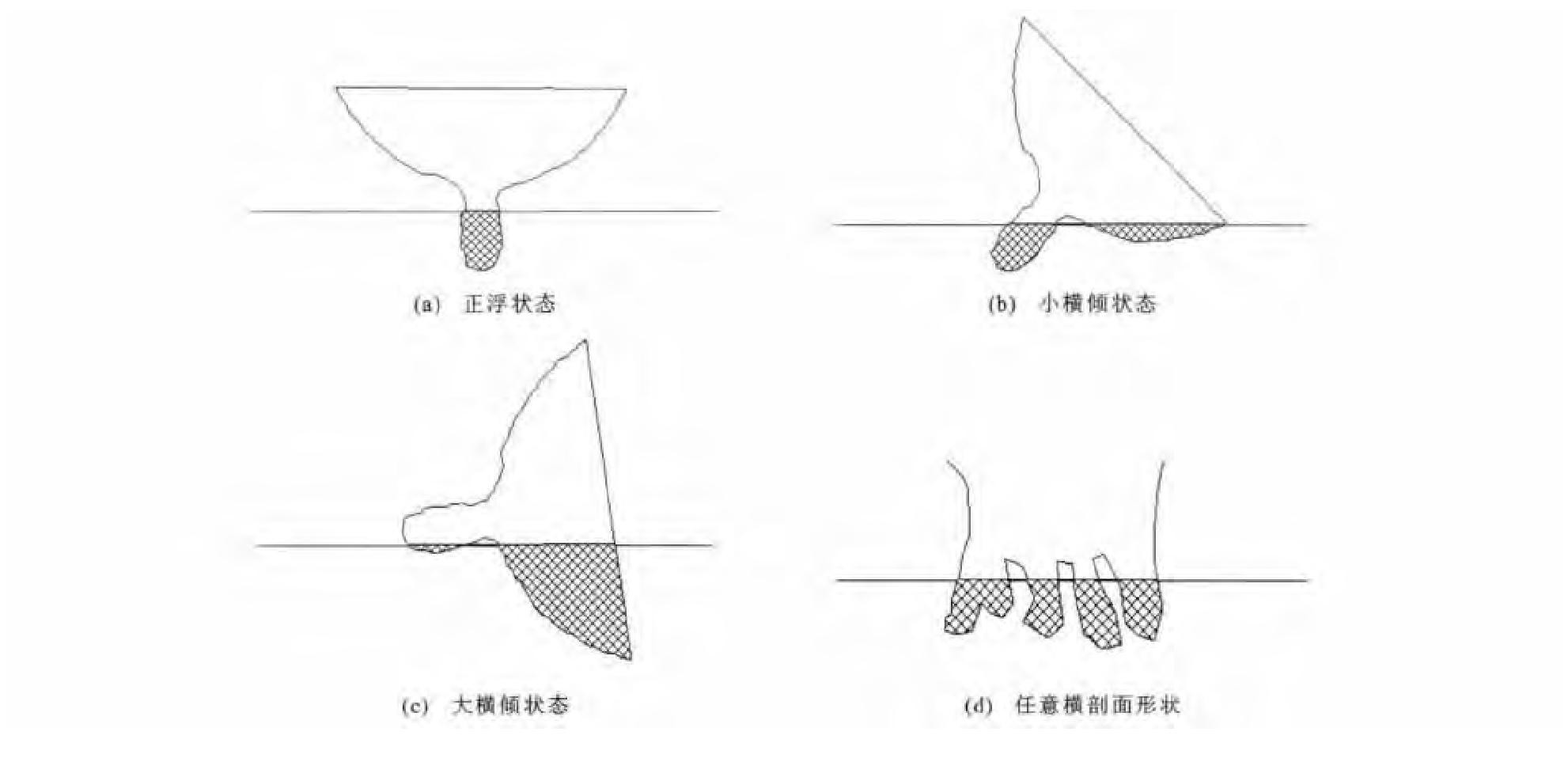
编写VC++程序验证S-H剪裁算法。图 15 (a)~(c)分别为散货船舶太行128某横剖面在正浮、小横倾与大横倾状态下与水线面交点情况, 图 15 (d)为任意横剖面形状与水线面的交点情况。结果表明S-H剪裁算法通用性好, 适用于任何船舶自由浮态的情况, 包括破损船、双体船等特殊结构船舶。
3. 计算结果分析
以散货船太行128为例, 分别计算了船舶在正浮、纵倾与中拱状态的排水量, 结果见表 2~4。
表 2 船舶正浮时水尺计重结果Table 2. Draft survey results of ship in even keel condition 表 3 船舶纵倾时水尺计重结果Table 3. Draft survey results of ship in trim condition
表 3 船舶纵倾时水尺计重结果Table 3. Draft survey results of ship in trim condition 表 4 船舶中拱时水尺计重结果Table 4. Draft survey results of ship in hogging condition
表 4 船舶中拱时水尺计重结果Table 4. Draft survey results of ship in hogging condition
表 2为船舶正浮时的计算结果, 2种计算结果相对误差均较小, 因为传统方法计算时纵倾修正和拱垂修正都为0, 查表时误差较小, 船舶吃水为7~9m时本文方法的相对误差分别为0.096 4%、0.085 0%、0.075 5%, 平均为0.085 6%。可见船舶正浮时用传统的水尺计重方法和本文改进方法均能得到正确的结果。
表 3为船舶无拱垂, 但有纵倾时的水尺计重计算结果, 以吃水分别为5、6、7 m的情况为例, 吃水差分别为-1、-2、-3 m。随着纵倾的增大, 相对误差逐渐增大, 当吃水差为-3m时, 平均相对误差增大到0.414 5%, 可见传统方法会产生较大误差。
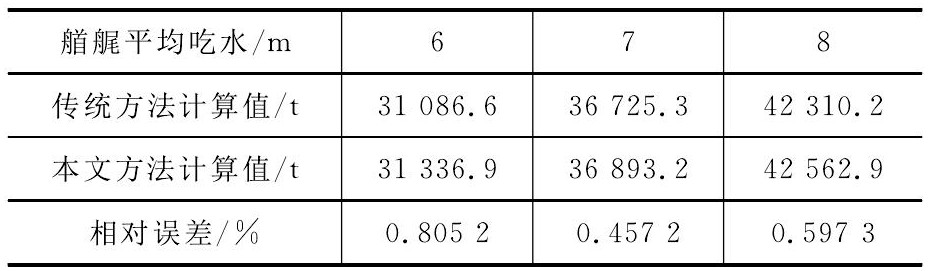
表 4为船舶正浮但有拱垂时的计算结果, 拱垂值δ取正常值为0.17m, 属于船舶正常的拱垂变形范围, 但吃水分别为5、6、7m时, 其平均相对误差增加到0.619 9%, 这在实际水尺计重是不能接受的。
综上可知, 船舶在纵倾与拱垂状态下, 采用传统方法计算平均吃水和本文方法计算结果的相对误差较大, 理论上本文的计算结果更接近于船舶真实排水量, 方法适用于船舶自由浮态。
4. 结语
相比传统的查取静水力表的水尺计重方法, 本文方法有如下改进: 通过坐标平移量化了船舶拱垂变形, 比传统拱垂修正精度高; 通过矩阵变换和水线面求交计算排水量, 对船舶的浮态没有限制, 且计算精度较高, 有一定的实际应用价值。本文方法需要船舶设计部门提供加密的数字型值表, 对于只能提供普通型值表的需要插值加密, 未来将进一步研究普通型值表的加密及液位遥测系统与本文方法相结合的完整的水尺计重系统。
-
表 1 计算误差对比
Table 1. Comparison of calculation errors
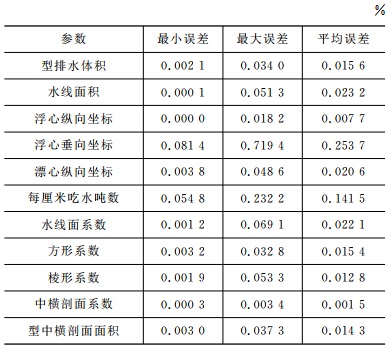
表 2 船舶正浮时水尺计重结果
Table 2. Draft survey results of ship in even keel condition
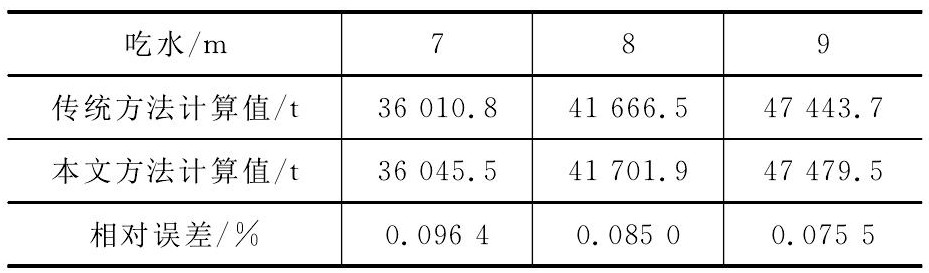
表 3 船舶纵倾时水尺计重结果
Table 3. Draft survey results of ship in trim condition
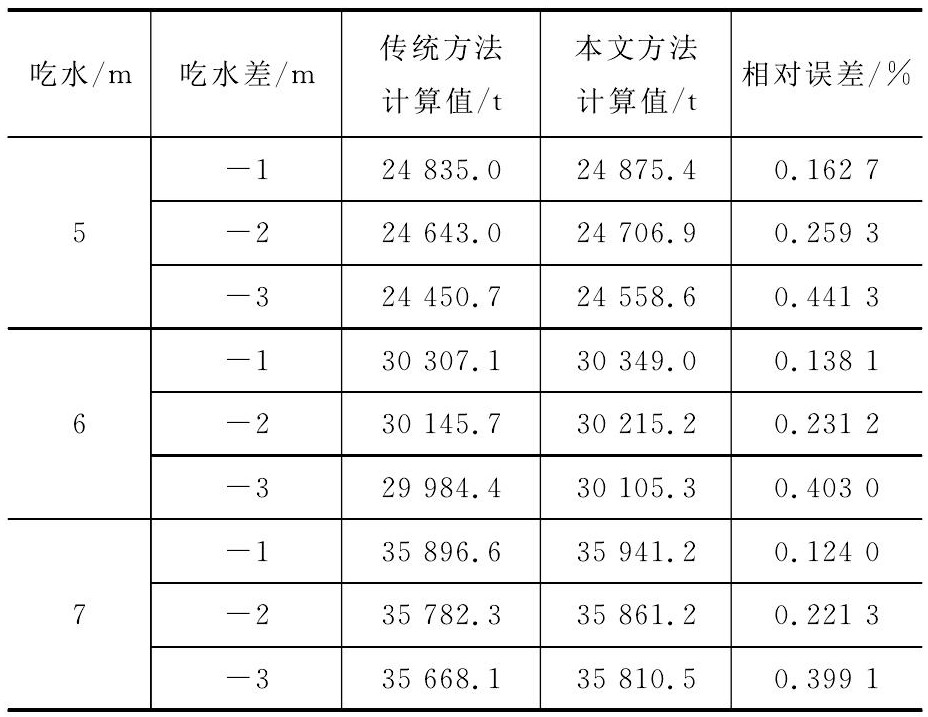
表 4 船舶中拱时水尺计重结果
Table 4. Draft survey results of ship in hogging condition
-
[1] 郑士源, 姚祖洪. 国际干散货航运市场的评价[J]. 交通运输工程学报, 2004, 4 (4): 88-92. doi: 10.3321/j.issn:1671-1637.2004.04.022ZHENG Shi-yuan, YAO Zu-hong. Evaluation of international dry bulk shipping market[J]. Journal of Traffic and Transportation Engineering, 2004, 4 (4): 88-92. (in Chinese). doi: 10.3321/j.issn:1671-1637.2004.04.022 [2] 林火平. 散货船水尺检量中计算所得船舶常数的误差[J]. 航海技术, 1996 (6): 26-27. https://www.cnki.com.cn/Article/CJFDTOTAL-HHJS199606012.htmLIN Huo-ping. The constant error of bulk carrier draft survey[J]. Marine Technology, 1996 (6): 26-27. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-HHJS199606012.htm [3] 王淑敏, 方卫东. 水尺计重实施中几个问题的研究[J]. 大连海事大学学报, 1998, 24 (1): 79-82. https://www.cnki.com.cn/Article/CJFDTOTAL-DLHS801.018.htmWANG Shu-min, FANG Wei-dong. Research on the deviation and calibration of constant in draft survy[J]. Journal of Dalian Maritime University, 1998, 24 (1): 79-82. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-DLHS801.018.htm [4] 陈建锋. 影响散货船压载水准确测算的因素[J]. 航海技术, 2003 (5): 20-22. doi: 10.3969/j.issn.1006-1738.2003.05.013CHEN Jian-feng. Element of influence of ballast water sounding and calculation[J]. Marine Technology, 2003 (5): 20-22. (in Chinese). doi: 10.3969/j.issn.1006-1738.2003.05.013 [5] 李清林. 水尺检量中吃水差和船舶长度适用问题的分析[J]. 世界海运, 2007, 30 (3): 41-42. doi: 10.3969/j.issn.1006-7728.2007.03.016LI Qing-lin. Correspondence of ship's length and trim in draft survey calculation[J]. Word Shipping, 2007, 30 (3): 41-42. (in Chinese). doi: 10.3969/j.issn.1006-7728.2007.03.016 [6] 黄昱洪. 大纵倾情况下船舶排水量的精确测定[J]. 中国水运, 2009, 9 (7): 34-35. doi: 10.3969/j.issn.1006-7973-B.2009.07.020HUANG Yu-hong. Accurate determination of tonnage in large trim condition[J]. China Water Transport, 2009, 9 (7): 34-35. (in Chinese). doi: 10.3969/j.issn.1006-7973-B.2009.07.020 [7] 刘辉强. 水尺计重及其误差分析[D]. 大连: 大连海事大学, 2010.LIU Hui-qiang. Draft survey and error analysis[D]. Dalian: Dalian Maritime University, 2010. (in Chinese). [8] RAN Xin, SHI Chao-jian, CHEN Jin-biao, et al. Draft line detection based on image processing for dhip draft survey[C]∥GAOL F L, NGUYEN Q V. Proceedings of the 2011 2nd International Congress on Computer Applications and Computational Science. Warszawa: Springer, 2011: 39-44. [9] GU Hong-wei, ZHANG Wang, XU Wen-hai, et al. Digital measurement system for ship draft survey[J]. Applied Mechanics and Materials, 2013, 333-335: 312-316. doi: 10.4028/www.scientific.net/AMM.333-335.312 [10] ZIHA K. Displacement of a deflected ship hull[J]. Marine Technology and Sname News, 2002, 39 (1): 54-63. doi: 10.5957/mt1.2002.39.1.54 [11] IVCE R, JURDANA I, MOHOVIC R. Determining weight of cargo onboard ship by means of optical fibre technology draft reading[J]. PROMET—Traffic and Transportation, 2011, 23 (6): 421-429. [12] 刘春雷, 张秀凤, 孙霄峰, 等. 基于加密型值表的船舶静水力特性精确计算[J]. 中国造船, 2013, 54 (4): 163-172. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC201304022.htmLIU Chun-lei, ZHANG Xiu-feng, SUN Xiao-feng, et al. Hydrostatic performance calculation of vessel based on densified table of offsets[J]. Shipbuilding of China, 2013, 54 (4): 163-172. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC201304022.htm [13] 刘春雷. 散货船智能化配载仪的研究与实现[D]. 大连: 大连海事大学, 2013.LIU Chun-lei. Research and implementation of intelligent bulk carrier stowage system[D]. Dalian: Dalian Maritime University, 2013. (in Chinese). [14] 陆丛红, 林焰, 纪卓尚. 基于NURBS表达的船舶静水力特性精确计算[J]. 船舶力学, 2007, 11 (5): 691-701. doi: 10.3969/j.issn.1007-7294.2007.05.006LU Cong-hong, LIN Yan, JI Zhuo-shang. Precise calculation of ship hydrostatic performances based on NURBS shipform[J]. Journal of Ship Mechanics, 2007, 11 (5): 691-701. (in Chinese). doi: 10.3969/j.issn.1007-7294.2007.05.006 [15] 陆丛红, 林焰, 纪卓尚. 基于曲面表达的几何特性计算及其在船舶工程中的应用[J]. 哈尔滨工程大学学报, 2005, 26 (6): 697-703. doi: 10.3969/j.issn.1006-7043.2005.06.001LU Cong-hong, LIN Yan, JI Zhuo-shang. Geometric properties calculation based on surface representation and its application to ship engineering[J]. Journal of Harbin Engineering University, 2005, 26 (6): 697-703. (in Chinese). doi: 10.3969/j.issn.1006-7043.2005.06.001 [16] 赵晓非, 林焰. 关于解船舶浮态问题的矩阵方法[J]. 中国造船, 1985, 26 (3): 55-64. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC198503005.htmZHAO Xiao-fei, LIN Yan. Matrix methods for solving ship floating state problem[J]. Shipbuilding of China, 1985, 26 (3): 55-64. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGZC198503005.htm [17] 林焰, 李铁骊, 纪卓尚. 破损船舶自由浮态计算[J]. 大连理工大学学报, 2001, 41 (1): 85-89. doi: 10.3321/j.issn:1000-8608.2001.01.019LIN Yan, LI Tie-li, JI Zhuo-shang. Ship damage floating calculation[J]. Journal of Dalian University of Technology, 2001, 41 (1): 85-89. (in Chinese). doi: 10.3321/j.issn:1000-8608.2001.01.019 [18] MAILLOT P G. A new, fast method for 2Dpolygon clipping: analysis and software implementation[J]. ACM Transactions on Graphics, 1992, 11 (3): 276-290. doi: 10.1145/130881.130894 [19] RAPPOPORT A. An efficient algorithm for line and polygon clipping[J]. The Visual Computer, 1991, 7 (1): 19-28. doi: 10.1007/BF01994114 -






 下载:
下载:















 下载:
下载: