Analysis method on time-history characteristics of rail supporting force for mixed passenger and freight railway with ballastless track
-
摘要: 采用Tekscan压力测量系统现场测试了遂宁—重庆客货共线无砟轨道钢轨支点压力, 提出了高斯函数型钢轨支点压力时程表达式, 并通过现场实测数据对其进行验证; 根据钢轨支点压力时程表达式, 采用时序式加载法对轨道结构模型施加荷载, 并将其动力响应结果分别与车辆-轨道-路基垂向耦合振动模型的计算结果和现场实测结果进行对比。研究结果表明: 现场实测客货车对钢轨支点的最大压力分别为29.91和82.49 kN, 与中国铁道科学研究院测试结果的相对误差小于20%, 故Tekscan压力测量系统可精确测试钢轨支点压力; 高斯函数拟合所得客货车对钢轨支点压力的时程曲线与实测曲线的相关系数分别为0.962 7和0.966 7, 最大压力与现场实测值的相对差异分别为5.15%和0.46%, 最小压力与现场实测值的相对差异分别为7.23%和24.11%, 故采用高斯函数能较好地模拟客货车对钢轨支点压力的时程曲线, 且货车作用下钢轨支点压力时程的模拟精度略高于客车; 基于时序式加载法的荷载激励-轨道-路基模型计算结果与车辆-轨道-路基垂向耦合振动模型计算结果和现场测试结果相比, 轨道板最大位移相对差异分别为5.41%和2.70%, 底座板最大位移相对差异分别为2.86%和5.71%, 轨道板最大加速度相对差异分别为14.00%和23.20%, 底座板最大加速度相对差异分别为13.61%和8.73%。可见, 基于时序式加载法和高斯函数型钢轨支点压力时程表达式的荷载激励-轨道-路基模型可靠, 该方法无需建立车体模型, 既能保证计算效率, 又具有很高的精度。Abstract: The rail supporting force for mixed passenger and freight railway with ballastless track in the Suining to Chongqing Railway was tested on site by the Tekscan pressure measurement system. A Gaussian function type time-history expression of rail supporting force was proposed and verified by the field test data. According to the time-history expression of rail supporting force, the loads were applied to the track structure model through the sequential loading method, and the dynamic response results were compared with those obtained from the vehicle-track-subgrade vertical coupling vibration model and the field test. Research result shows that the maximum field measured rail supporting forces of passenger and freight train are 29.91 and 82.49 kN, respectively. The relative differences are less than 20% in comparison with the test result obtained by the China Academy of Railway Sciences. Therefore, the Tekscan pressure measurement system can accurately measure the rail supporting force. For the passenger and freight train, the correlation coefficients of rail supporting force time-history curves fitted by the Gaussian function and the field measured curves are 0.962 7 and 0.966 7, respectively. The relative differences between the fitted maximum rail supporting forces and the field measured values are 5.15% and 0.46%, respectively, and the relative differences between the fitted minimum rail supporting forces and the field measured values are 7.23% and 24.11%, respectively. Therefore, the Gaussian function can well simulate the time-history curves of rail supporting force under the actions of passenger and freight trains, and the simulation accuracy to freight train is slightly higher than to passenger train. Compared with the results of vehicle-track-subgrade vertical coupling vibration model and field test, the relative differences of the maximum displacements of track slab obtained from the load excitation-track-subgrade model based on the sequential loading method are 5.41% and 2.70%, respectively, the relative differences of the maximum displacements of base plate are 2.86% and 5.71%, respectively, the relative differences of the maximum acceleration of track slab are 14.00% and 23.20%, respectively, and the relative differences of the maximum accelerations of base plate are 13.61% and 8.73%, respectively. Therefore, the load excitation-track-subgrade model based on the sequential loading method and the Gaussian function type time-history expression of rail supporting force is reliable. This method does not need to establish the car body model, and not only ensure the calculation efficiency, but also have a very high accuracy.
-
0. 引言
为缓解铁路运输压力, 客运专线运营前期和部分既有线路提速完成后均采用客货共线模式[1]。与客运专线不同的是, 货车运营具有轴重大、运量大的特点[2, 3, 4], 且客货共线无砟轨道的列车荷载作用存在频率变换, 表现为大小不同的复杂特征。在分析轨道结构动力响应时, 如何考虑列车荷载是关键问题[5, 6], 因此, 数值模拟或模型试验的合理性取决于列车动荷载的施加方式。扣件是影响无砟轨道结构安全性的重要构件[7, 8], 轨道结构直接承受列车动荷载的作用, 并通过扣件以钢轨支点压力的形式作用于轨道板, 故有必要得到钢轨支点压力时程表达式。
针对钢轨支点压力问题, 国内外学者已做了较多理论分析。在列车荷载现场实测方面, 已产生多种现场测试轮轨力的方法[9, 10, 11, 12, 13, 14], 而对于钢轨支点压力的测试方法较少。蒋红光通过在轨道板扣件正下方的轨道板表面粘贴应变片, 测量了板式无砟轨道试验模型的钢轨支点压力[15]; 徐家铎等选取WJ-7B型板式无砟轨道扣件胶垫自制测力垫板, 并应用东华动态信号采集分析系统现场测试了钢轨支点压力[1]; 对于钢轨支点压力时程特性, Bian等建立了足尺板式轨道路基模型, 通过多个激振器的协同作用来模拟列车荷载, 并通过千分表测得了荷载作用下的钢轨变形, 从而得到了扣件荷载分担比[16]; 黄瑛建立了无砟轨道室内模型, 研究了钢轨支点压力与列车运行速度和轮载的关系[17]; 戴林发宝采用列车-轨道动力分析模型计算了高速列车不同速度下的钢轨支点压力时程曲线[18]; 陈希成等利用ANSYS建立轨道板模型, 研究了不同速度移动荷载作用下钢轨支点压力时程曲线[19]; 周小壮利用有限元软件建立CRTS Ⅱ型板式无砟轨道模型, 通过移动集中荷载法模拟列车动态荷载, 得到了列车在不同速度和轴重下的钢轨支点压力时程曲线[20]; 邵鸣和以轮轨系统动力学为基础, 通过列车-轨道垂向耦合模型得到了沿线路方向的钢轨支点压力时程曲线, 并将其输入到轨道-路基-地基有限元模型中, 研究了地面振动规律[21]; 王晅等建立了轨道-路基有限元模型, 并根据列车荷载的特点, 采用Fourier变换得到了2个转向架作用下的钢轨支点压力时程曲线, 还利用现场实测数据对该方法进行了验证[22]; 朱胜阳等通过建立车辆-轨道耦合动力分析模型, 得到了钢轨支点压力时程曲线, 并以此作为外部激励, 分析了双块式无砟轨道道床板伤损特性[23]。
上述学者仅从室内试验和数值模拟方面研究了钢轨支点压力, 缺乏现场实测数据与理论仿真的相互验证。鉴于此, 本文首先提出高斯函数型钢轨支点压力时程表达式, 并通过重庆—怀化(渝怀) 铁路线和遂宁—重庆(遂渝) 铁路线现场动力测试所得钢轨支点压力数据验证其可靠性; 然后根据时程表达式, 并应用时序式加载法对轨道-路基模型施加荷载, 最后将其动力响应结果分别与车辆-轨道-路基垂向耦合振动模型的计算结果和现场测试结果进行对比, 以验证此方法的可行性。
1. 客货共线钢轨支点压力时程特性拟合与验证
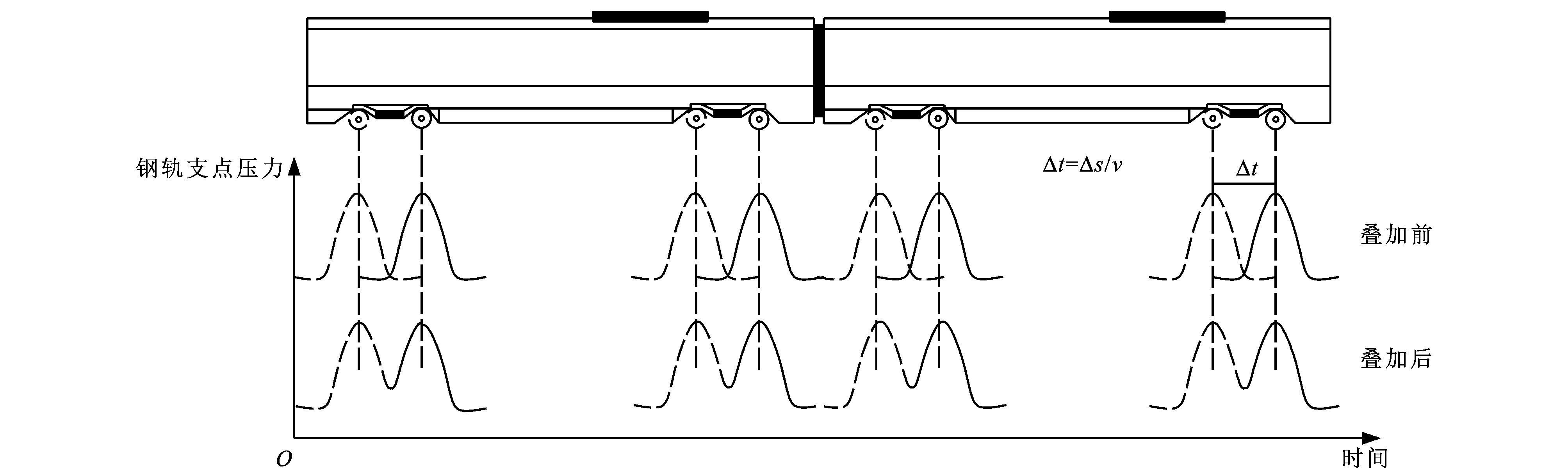
客货共线无砟轨道的列车荷载情况较为复杂。客货车运行时, 列车荷载经扣件系统传递至轨道结构和下部路基, 扣件将荷载转化为竖向激励。鉴于列车荷载模拟是轨道-路基模型试验的关键问题之一, 蒋红光等提出了时序式加载法[24], 即将扣件系统的荷载时程按一定时间间隔依次施加到钢轨支点上, 见图 1。使用该方法时须获得列车荷载作用下钢轨支点压力的时程曲线。
由ψ=F/P (ψ为扣件荷载分担比; F为扣件处钢轨支点压力; P为列车与钢轨间的作用力) 可知: 钢轨支点压力时程表达式的函数类型和扣件荷载分担比相同, 故可先确定扣件荷载分担比的时程表达式。
1.1 扣件荷载分担比函数拟合
由文克尔假设[25]可知, 在任意位置由轮载作用产生的基础反力p为
p=Q2Le-x-x0L cos(x-x0L)+sin(x-x0L) (1)
L=4√4EΙ/k (2)
式中: Q为轮载; x为车轮作用位置; x0为扣件所在位置; L为钢轨特征长度; E、I分别为钢轨的弹性模量和截面抗弯惯性矩; k为连续弹性地基的弹性系数。
对2组扣件间距内的基础反力进行积分, 得出x0处扣件的钢轨支点压力F为
F=∫x-x0+b2x-x0-b2pdx (3)
式中: b为扣件间距离。
根据式(3) 的积分结果, 扣件处钢轨支点压力F和扣件荷载分担比ψ分别为
F=0.5Q[-e-x-x0+0.5bLcos(x-x0+0.5bL)+e-x-x0-0.5bLcos(x-x0-0.5bL)] (4)
ψ=0.5[-e-x-x0+0.5bLcos(x-x0+0.5bL)+e-x-x0-0.5bLcos(x-x0-0.5bL)] (5)
式(5) 与高斯函数较为相似, 故采用高斯函数来拟合扣件荷载分担比, 即
ψ=y0+Ae-(x-x0)22w2 (6)
式中: y0、A、w均为拟合公式的计算参数, 取值分别为-0.003 5、0.450 0、0.680 0。
通过现场实测客货车对钢轨支点的压力可验证式(6) 的可靠性, 从而确定钢轨支点压力时程表达形式。
1.2 钢轨支点压力现场动力测试
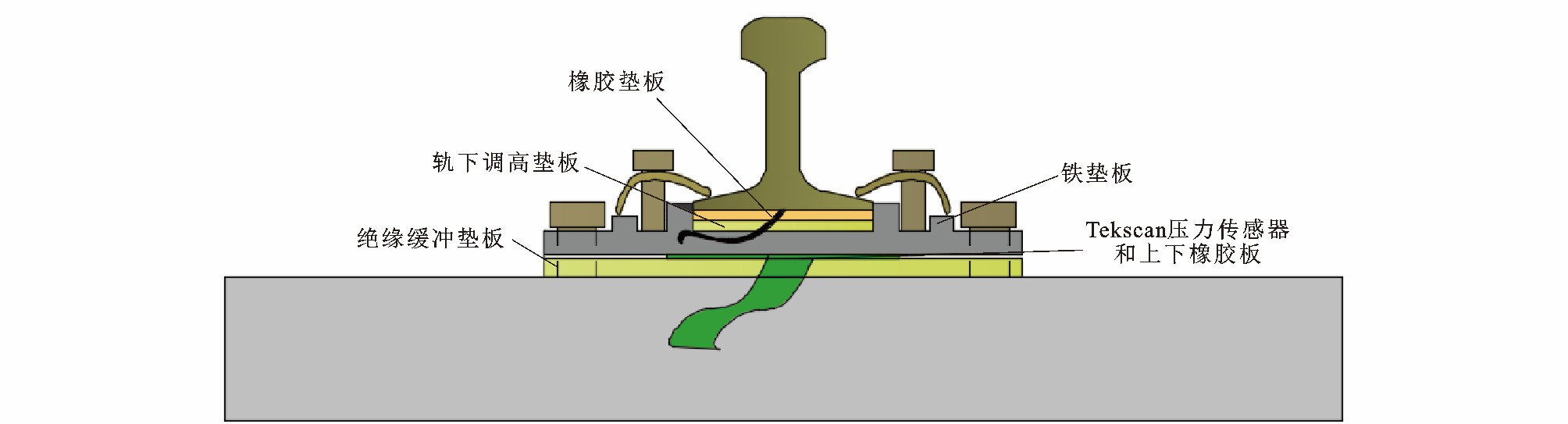
为获取客货共线运营条件下的列车荷载, 采用美国Tekscan压力测量系统现场测试渝怀线鱼嘴二号隧道长枕埋入式无砟轨道和遂渝线蔡家工区CRTS Ⅰ型板式无砟轨道。Tekscan中的压力传感器在测量系统中起至关重要的作用, 见图 2[26]。传感器布置见图 3, 将其放置于绝缘缓冲垫板和铁垫板之间。在现场试验前, 为使Tekscan压力传感器输出结果与施加荷载保持一致, 需预先对其标定, 传感器标定装置见图 4。
在现场安装传感器时, 将扣件螺栓去除, 利用千斤顶抬升钢轨, 将传感器放置在铁垫板和缓冲垫板之间, 最后拧紧扣件螺栓, 安装过程见图 5。
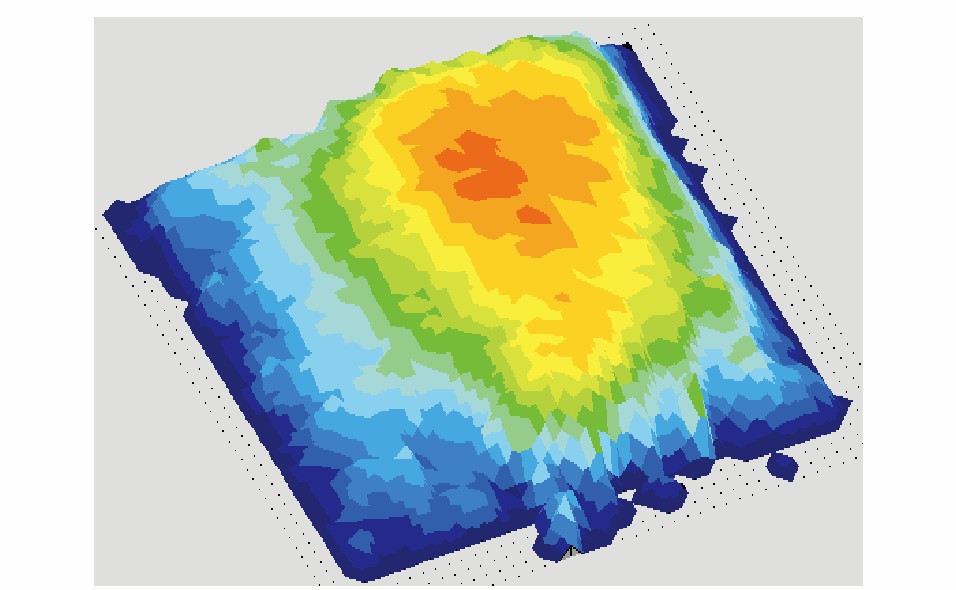
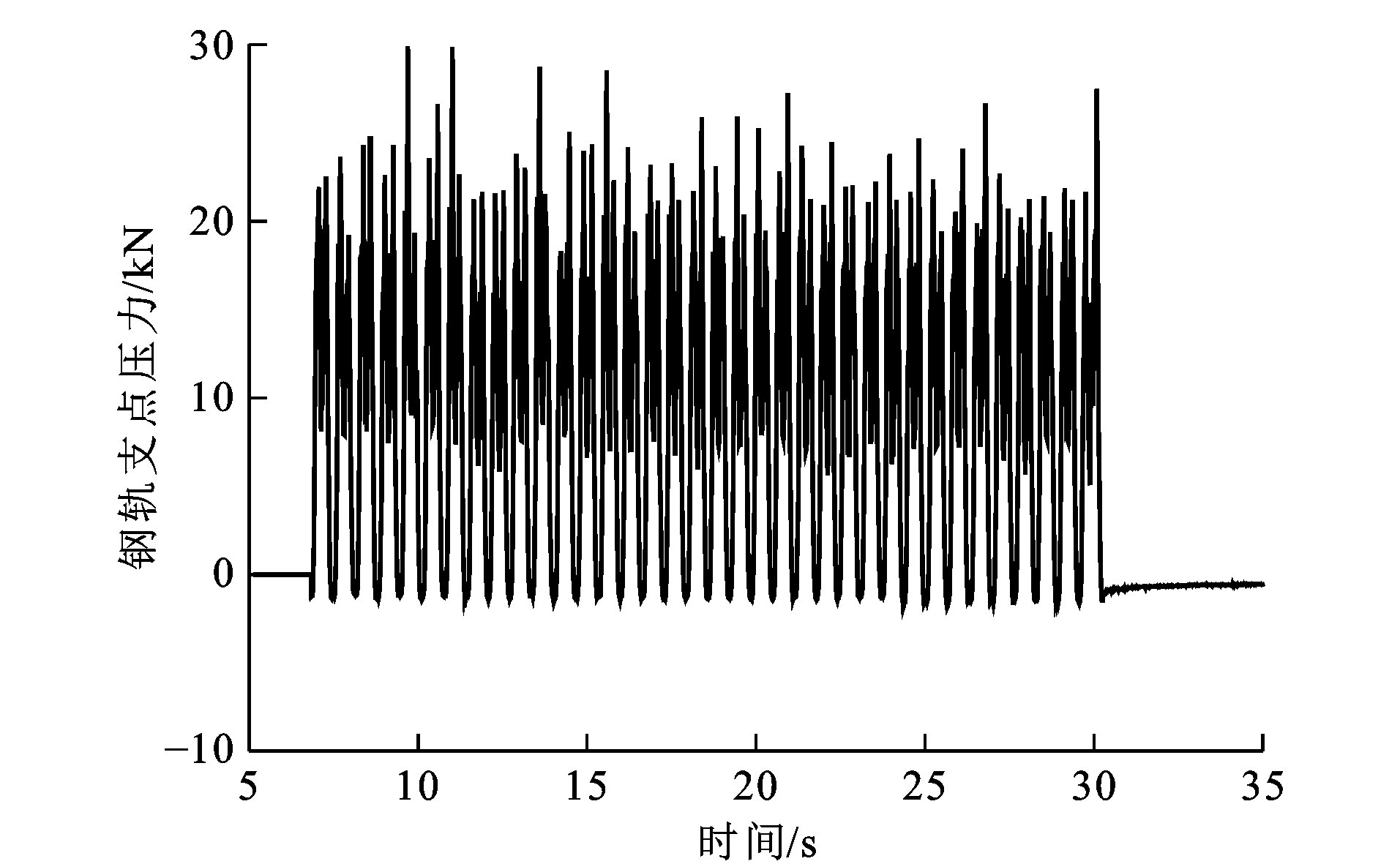
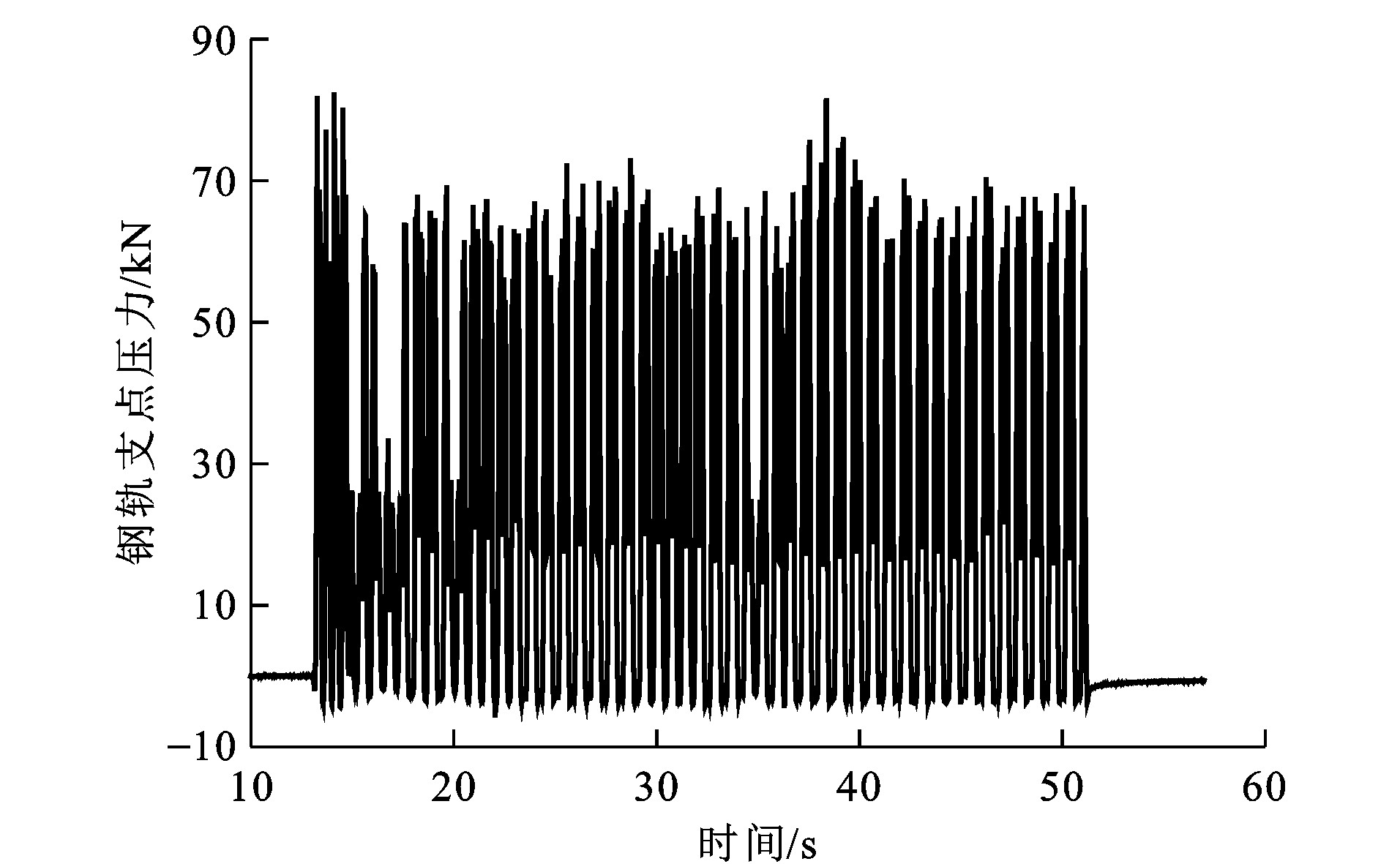
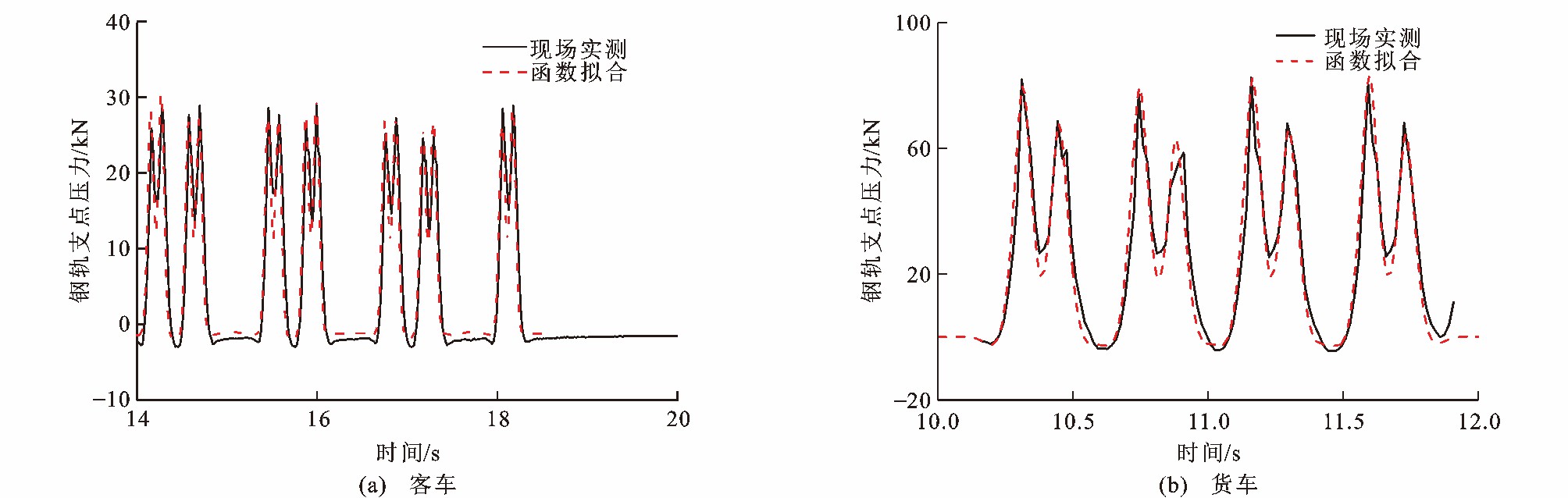
当列车经过测量位置的扣件时, 该测量系统会输出此时钢轨支点压力三维轮廓(图 6), 再经过内部积分运算处理生成钢轨支点压力, 三维轮廓可准确、直观地得出钢轨支点压力及其分布情况。通过整理列车经过时的多组钢轨支点压力数据, 即可得到遂渝线客货车作用下该扣件处钢轨支点压力的时程曲线, 分别见图 7、8, 可知: 客货车对钢轨支点的最大压力分别为29.91和82.49 kN, 与中国铁道科学研究院的测试结果(客货车对钢轨支点的压力峰值波动范围分别为27.91~39.47和50.71~78.83 kN) 相比, 误差基本在20%以内。
1.3 高斯函数型扣件荷载分担比可靠性验证
当多个轮载作用时, 任意扣件位置的钢轨支点压力可通过叠加作用进行计算[27], 见图 9, 其中: v为列车行驶速度; Δs为车轮之间的距离; Δt为车轮之间的时间差。
对于二轴转向架, 钢轨支点压力的时程表达式为
F=2∑i=1Ρiψi=Ρ1ψ1+Ρ2ψ2 (7)
式中: Pi为第i个车轮与钢轨之间作用力; ψi为第i个车轮作用时的扣件荷载分担比。
对于式(7), ψ1和ψ2分别为
{ψ1=y0+Ae-(x-j/2-x0)22w2ψ2=y0+Ae-(x+j/2-x0)22w2 (8)
式中: j为转向架两轮轴间的距离。
根据现场调研资料, 测试车型分别为车厢类型为25G的韶山7型客车和双机车牵引的和谐HXD1货车, 结构尺寸分别见图 10、11。
根据现场测试客货车轮轨力和高斯函数型荷载分担比公式可计算得单个车轮经过时提取点处的钢轨支点压力, 再通过叠加作用求出整车经过时钢轨支点压力的时程曲线, 并将此结果与现场实测结果对比, 即可验证高斯函数型扣件荷载分担比的可靠性。
钢轨支点压力的高斯函数拟合曲线与现场实测曲线的对比情况见图 12, 可知: 高斯函数拟合曲线与现场实测曲线基本重合, 其相关系数分别为0.962 7和0.966 7;高斯函数拟合与现场实测客车对钢轨支点的最大压力分别为31.45、29.91 kN, 相对误差为5.15%, 货车对钢轨支点的最大压力分别为82.11、82.49 kN, 相对误差为0.46%;高斯函数拟合与现场实测客车对钢轨支点的最小压力分别为11.67、12.58 kN, 相对误差为7.23%, 货车对钢轨支点的最小压力分别为19.30、25.43 kN, 相对误差为24.11%。综上所述, 高斯函数能较好地模拟客货车作用下钢轨支点压力时程曲线, 且对货车的模拟精度略高于客车。
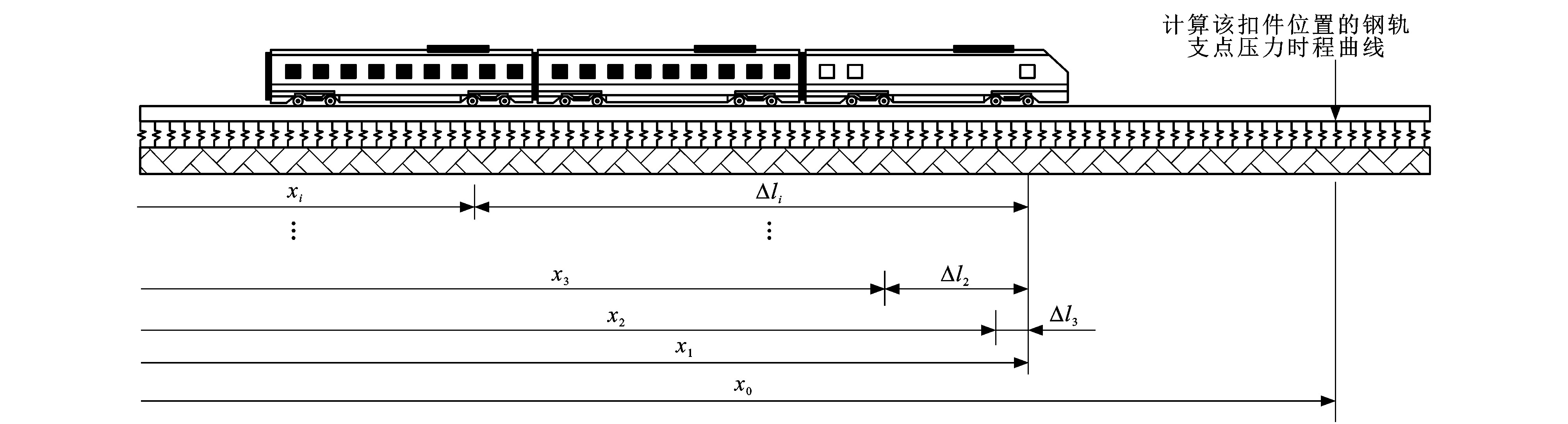
当列车经过目标扣件时, 钢轨支点压力时程表达式见式(9), 其现场示意见图 13
F=n∑i=1Qiψi=n∑i=1Qi y0+Ae-(vt-vΔti-x0)22w2 (9)
Δti=Δli/v (10)
式中: xi为列车第i个车轮的位置; Δli为列车第i个车轮与第1个车轮的间距; n为列车车轮数; t为时间; Δti为列车运行Δli所用时间。
2. 客货共线钢轨支点压力时程特性适用性
将钢轨支点压力时程表达式作为荷载激励导入基于ANSYS瞬态动力学建立的轨道-路基有限元模型中, 采用时序式加载法将计算得到的钢轨支点压力施加在轨道板上的扣件处, 各扣件处施加的钢轨支点压力都为与时间相关的函数(式(9))。通过将其与基于ANSYS/SIMPACK联合仿真建立的车辆-轨道-路基垂向耦合振动模型的计算结果和现场测试结果对比, 分析钢轨支点压力时程表达式在有限元计算中的适用性, 并对时序式加载法进行验证。模型分别见图 14、15。
在车辆-轨道-路基垂向耦合振动模型中, 车辆选用中国CRH2型动车组, 其计算参数见表 1[28]。为简化模型, 将车辆视为刚体, 各部件间的联系视为弹性或刚性约束。
轨道结构为路基上CRTS Ⅰ型板式无砟轨道, 各部件主要参数见表 2[29]。钢轨简化为弹性欧拉梁, 扣件采用弹簧阻尼单元模拟, 轨道板和底座板采用实体单元模拟, CA砂浆采用非线性弹簧-阻尼单元模拟。在荷载激励-轨道-路基模型中, 轨道板、砂浆和底座板均采用实体单元模拟, 采用表面效应单元来替代路基对轨道结构的作用。
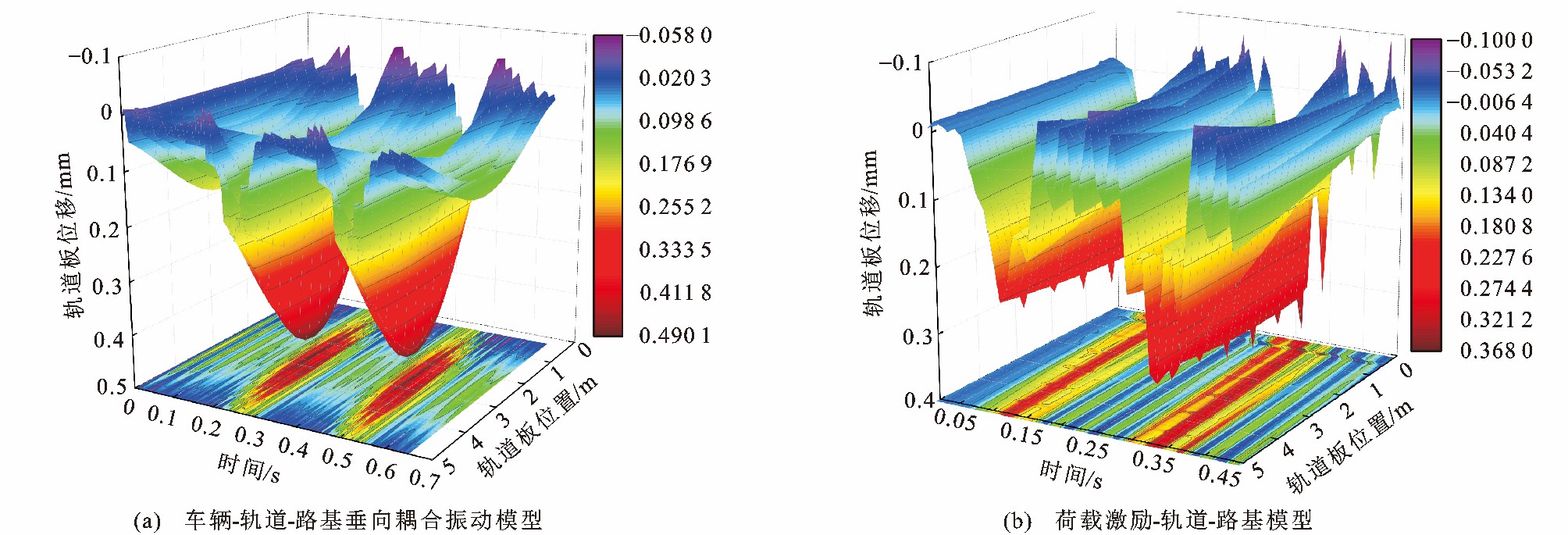
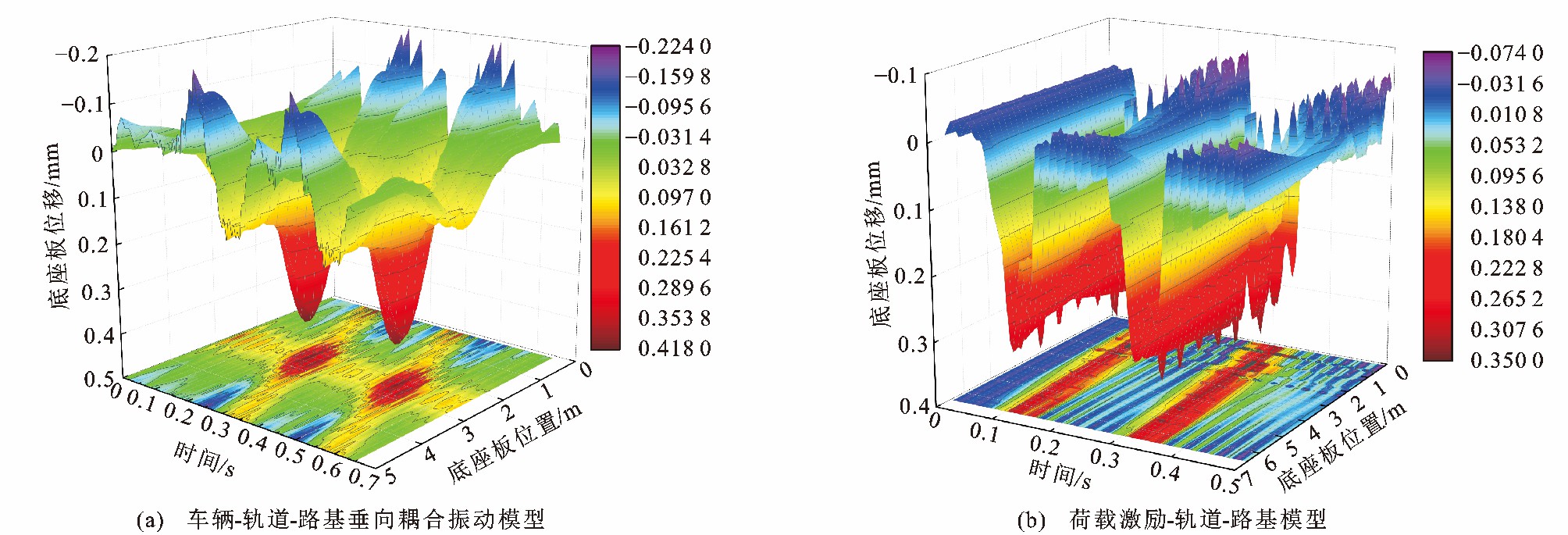
表 1 CRH2动车组计算参数Table 1. Calculation parameters of CRH2 MU参数 CRH2型车 车体质量/kg 39 600 转向架质量/kg 3 500 轮对质量/kg 2 000 车体点头惯量/ (kg·m2) 1.94×106 转向架点头惯量/ (kg·m2) 1.75×103 一系悬挂刚度/ (N·m-1) 1.18×106 一系悬挂阻尼/ (N·s·m-1) 1.89×106 二系悬挂刚度/ (N·m-1) 1.96×104 二系悬挂阻尼/ (N·s·m-1) 4.00×104 表 2 CRTS Ⅰ型板式无砟轨道结构计算参数Table 2. Calculation parameters of CRTS Ⅰ ballastless slab track structure部件 参数 取值 部件 参数 取值 钢轨 每延米质量/kg 60 路基 面刚度/ (MPa·m-1) 76 扣件 阻尼/ (kN·s·m-1) 20 CA砂浆 阻尼/ (kN·s·m-1) 270 动刚度/ (kN·mm-1) 50 弹性模量/MPa 300 间距/m 0.629 厚度/m 0.05 轨道板 弹性模量/MPa 3.65×104 底座板 弹性模量/MPa 3.25×104 长度/m 4.96 宽度/m 3.0 宽度/m 2.40 厚度/m 0.3 厚度/m 0.19 泊松比 0.2 车辆-轨道-路基垂向耦合振动模型和荷载激励-轨道-路基模型计算得到的轨道板和底座板位移分别见图 16、17, 可知: 车辆-轨道-路基垂向耦合振动模型和荷载激励-轨道-路基模型计算得到的轨道板最大位移分别为0.35和0.37 mm, 相对差异为5.41%, 底座板最大位移分别为0.34和0.35 mm, 相对差异为2.86%。
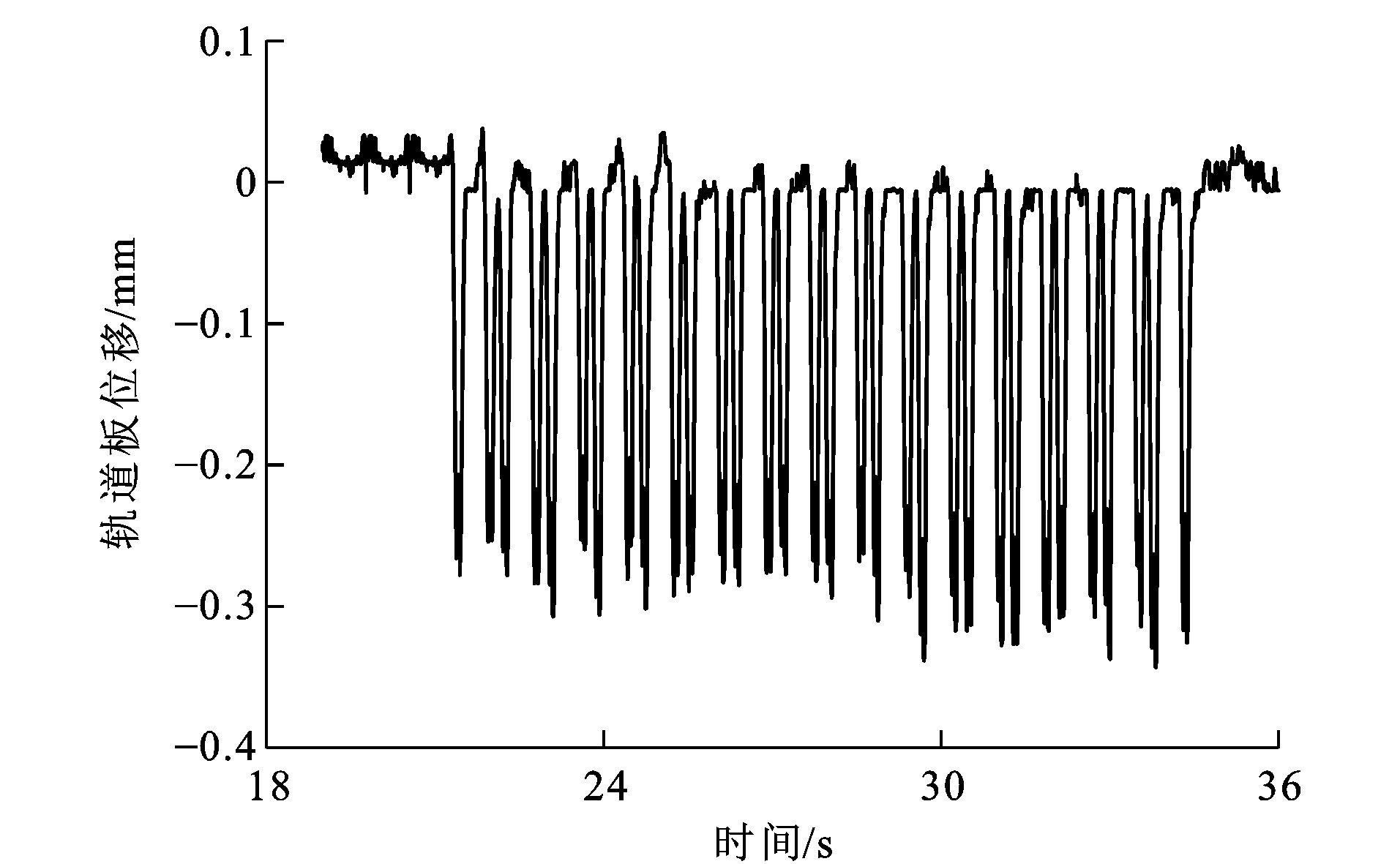
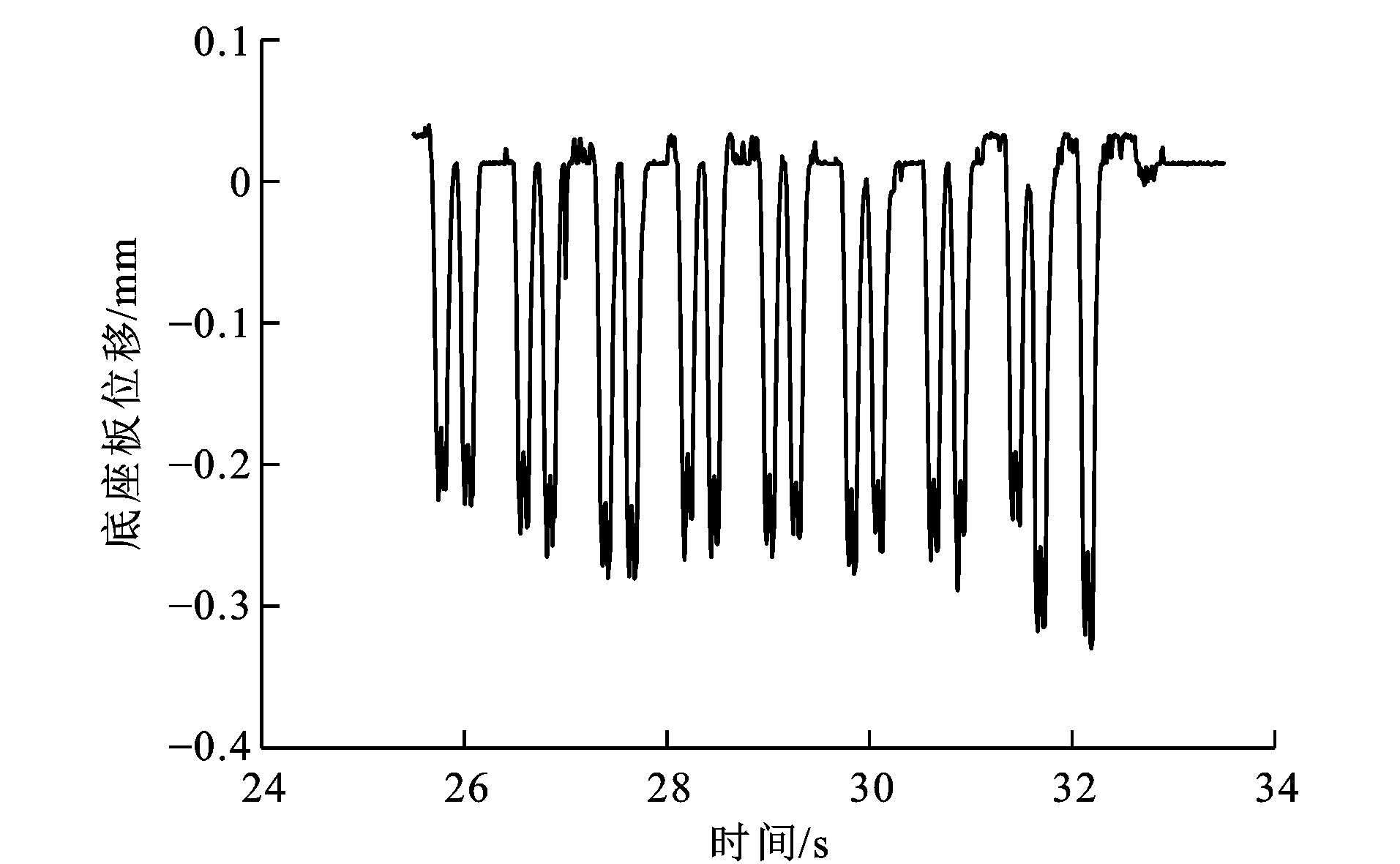
遂渝线客车作用下现场实测轨道板和底座板最大位移分别见图 18、19, 可知: 实测轨道板和底座板最大位移分别为0.38和0.33 mm, 与荷载激励-轨道-路基模型计算结果的相对差异分别为2.70%和5.71%。
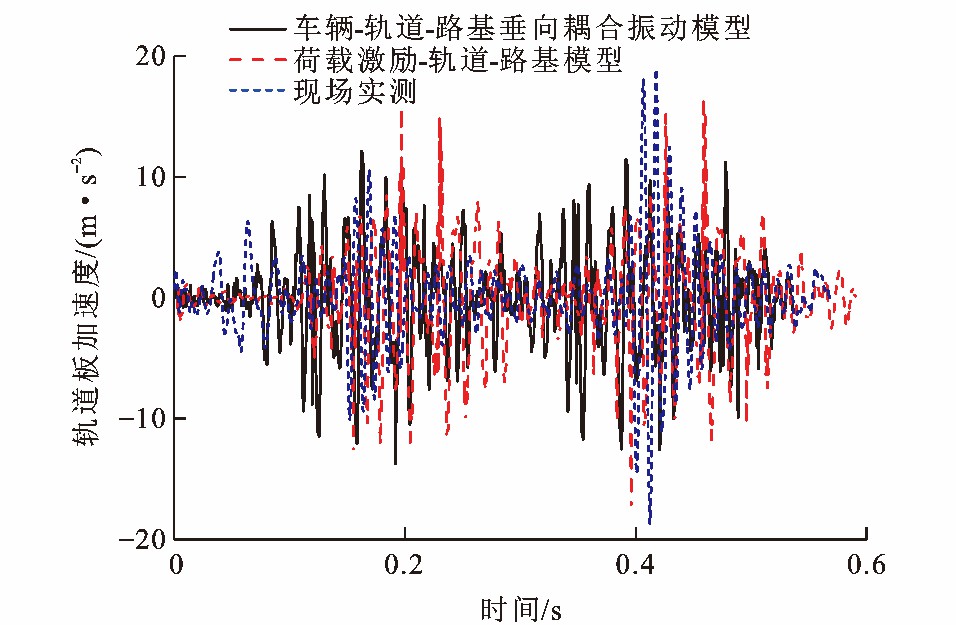
车辆-轨道-路基垂向耦合振动模型和荷载激励-轨道-路基模型计算得到的轨道板和底座板加速度与现场实测轨道板和底座板加速度分别见图 20、21, 可知: 车辆-轨道-路基垂向耦合振动模型和荷载激励-轨道-路基模型计算得到的轨道板最大加速度分别为17.59和15.43 m·s-2, 相对差异为14.00%, 底座板最大加速度分别为14.19和12.49 m·s-2, 相对差异为13.61%;现场实测轨道板和底座板最大加速度分别为19.01和13.58 m·s-2, 与荷载激励-轨道-路基模型计算结果的相对差异分别为23.20%和8.73%。
综上所述, 车辆-轨道-路基垂向耦合振动模型与荷载激励-轨道-路基模型的计算结果和现场测试的动力响应结果基本一致, 且采用这种建模方法模拟列车运行对轨道的作用时无需建立车体模型, 既能保证计算效率, 又具有很高的精度。
3. 结语
(1) 应用Tekscan压力测量系统能够较好地测试钢轨支点压力, 该方法使用方便, 测试精度高, 得出的客货车对钢轨支点的最大压力分别为29.91、82.49 kN。
(2) 钢轨支点压力的高斯函数拟合曲线与现场实测曲线基本重合, 曲线的相关系数分别为0.962 7和0.966 7, 故高斯函数能较好地模拟客货车对钢轨支点压力的时程曲线。
(3) 车辆-轨道-路基垂向耦合振动模型和荷载激励-轨道-路基模型计算得到的轨道板最大位移分别为0.35和0.37 mm, 相对差异为5.41%;底座板最大位移分别为0.34和0.35 mm, 相对差异为2.86%, 轨道板最大加速度分别为17.59和15.43 m·s-2, 相对差异为14.00%, 底座板最大加速度分别为14.19和12.49 m·s-2, 相对差异为13.61%;现场测试得到的轨道板和底座板最大加速度分别为19.01和13.58 m·s-2, 与荷载激励-轨道-路基模型计算结果的相对差异分别为23.20%和8.73%。可见, 采用时序式加载法, 并以钢轨支点压力时程作为荷载激励导入轨道-路基有限元模型来模拟列车运行对轨道的作用, 是研究轨道结构动力响应的有效方式。
(4) 后续将考虑轨道不平顺, 进一步验证高斯函数型钢轨支点压力时程表达式, 使该钢轨支点压力表达式更符合列车实际运行情况。
-
表 1 CRH2动车组计算参数
Table 1. Calculation parameters of CRH2 MU
参数 CRH2型车 车体质量/kg 39 600 转向架质量/kg 3 500 轮对质量/kg 2 000 车体点头惯量/ (kg·m2) 1.94×106 转向架点头惯量/ (kg·m2) 1.75×103 一系悬挂刚度/ (N·m-1) 1.18×106 一系悬挂阻尼/ (N·s·m-1) 1.89×106 二系悬挂刚度/ (N·m-1) 1.96×104 二系悬挂阻尼/ (N·s·m-1) 4.00×104 表 2 CRTS Ⅰ型板式无砟轨道结构计算参数
Table 2. Calculation parameters of CRTS Ⅰ ballastless slab track structure
部件 参数 取值 部件 参数 取值 钢轨 每延米质量/kg 60 路基 面刚度/ (MPa·m-1) 76 扣件 阻尼/ (kN·s·m-1) 20 CA砂浆 阻尼/ (kN·s·m-1) 270 动刚度/ (kN·mm-1) 50 弹性模量/MPa 300 间距/m 0.629 厚度/m 0.05 轨道板 弹性模量/MPa 3.65×104 底座板 弹性模量/MPa 3.25×104 长度/m 4.96 宽度/m 3.0 宽度/m 2.40 厚度/m 0.3 厚度/m 0.19 泊松比 0.2 -
[1] 徐家铎, 任娟娟, 闫亚飞, 等. 客货共线无砟轨道扣件垂向力现场测试与分析[J]. 铁道科学与工程学报, 2017, 14 (11): 2333-2338. doi: 10.3969/j.issn.1672-7029.2017.11.008XU Jia-duo, REN Juan-juan, YAN Ya-fei, et al. Field test and analysis of vertical force of fastener for slab track with passenger and freight traffic[J]. Journal of Railway Science and Engineering, 2017, 14 (11): 2333-2338. (in Chinese). doi: 10.3969/j.issn.1672-7029.2017.11.008 [2] 蔡成标, 翟婉明, 王开云. 遂渝线路基上板式轨道动力性能计算及评估分析[J]. 中国铁道科学, 2006, 27 (4): 17-21. doi: 10.3321/j.issn:1001-4632.2006.04.004CAI Cheng-biao, ZHAI Wan-ming, WANG Kai-yun. Calculation and assessment analysis of the dynamic performance for slab track on Sui-Yu Railway[J]. China Railway Science, 2006, 27 (4): 17-21. (in Chinese). doi: 10.3321/j.issn:1001-4632.2006.04.004 [3] 任娟娟, 徐家铎, 田根源, 等. 客货共线无砟轨道轮轨力统计特征研究[J]. 工程力学, 2018, 35 (2): 239-248. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201802029.htmREN Juan-juan, XU Jia-duo, TIAN Gen-yuan, et al. Field test and statistical characteristics of wheel-rail force for slab track with passenger and freight traffic[J]. Engineering Mechanics, 2018, 35 (2): 239-248. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201802029.htm [4] REN Juan-juan, DENG Shi-jie, WEI Kai, et al. Mechanical property deterioration of the prefabricated concrete slab in mixed passenger and freight railway tracks[J]. Construction and Building Materials, 2019, 208: 622-637. doi: 10.1016/j.conbuildmat.2019.03.039 [5] 梁波, 蔡英. 不平顺条件下高速铁路路基的动力分析[J]. 铁道学报, 1999, 21 (2): 84-88. doi: 10.3321/j.issn:1001-8360.1999.02.019LIANG Bo, CAI Ying. Dynamic analysis on subgrade of high speed railways in geometric irregular condition[J]. Journal of the China Railway Society, 1999, 21 (2): 84-88. (in Chinese). doi: 10.3321/j.issn:1001-8360.1999.02.019 [6] 任娟娟, 邓世杰, 闫亚飞, 等. 列车荷载致板式无砟轨道力学性能影响分析[J/OL]. 西南交通大学学报, 2018-05-22[2019-03-12]. http://kns.cnki.net/kcms/detail/51.1277.U.20180321.1956.022.html.RENJuan-juan, DENGShi-jie, YANYa-fei, etal. Influence of train load on the mechanical property of the prefabricated slab track [J/OL]. Journal of Southwest Jiaotong University, 2018-05-22[2019-03-12]. http://kns.cnki.net/kcms/detail/51.1277.U.20180321.1956.022.html. (inChinese). [7] LI Q T, LUO Y, LIU Y. Estimating clamping force of rail fastener system by experimental and numerical methods[J]. Transportation Research Procedia, 2017, 25: 443-450. doi: 10.1016/j.trpro.2017.05.424 [8] 韦凯, 王丰, 杨麒陆, 等. 钢轨扣件弹性垫板的宽频动力性能及其理论表征[J]. 铁道学报, 2019, 41 (2): 130-136. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201902019.htmWEI Kai, WANG Feng, YANG Qi-lu, et al. Broad frequency-domain dynamic properties of rail pad and its theoretical modal[J]. Journal of the China Railway Society, 2019, 41 (2): 130-136. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201902019.htm [9] ASKARINEJAD H, DHANASEKAR M, BOYD P, et al. Field measurement of wheel-rail impact force at insulated rail joint[J]. Experimental Techniques, 2015, 39 (5): 61-69. doi: 10.1111/j.1747-1567.2012.00867.x [10] STEENBERGENM J M M, DE JONG E, ZOETEMAN A. Dynamic axle loads as a main source of railway track degradation[J]. Geotechnical Safety and Risk V, 2015, 5: 243-249. [11] KATOU M, MATSUOKA T, YOSHIOKA O, et al. Numerical simulation study of ground vibrations using forces from wheels of a running high-speed train[J]. Journal and Sound Vibration, 2008, 318 (4/5): 830-849. [12] MEYMAND S Z, AHMADIAN M. Design, development, and calibration of a force-moment measurement system for wheel-rail contact mechanics in roller rigs[J]. Measurement, 2016, 81: 113-122. doi: 10.1016/j.measurement.2015.12.012 [13] 罗晶, 李斌, 全健健. 基于轮轨动态力测试的小半径曲线车辆运行安全性分析[J]. 兰州工业学院学报, 2015, 22 (5): 32-35. doi: 10.3969/j.issn.1009-2269.2015.05.007LUO Jing, LI Bin, QUAN Jian-jian. The operation safety analysis of vehicles on sharp-radius curve based on the test of dynamic wheel-rail forces[J]. Journal of Lanzhou Institute of Technology, 2015, 22 (5): 32-35. (in Chinese). doi: 10.3969/j.issn.1009-2269.2015.05.007 [14] 金鑫, 金新灿, 龚明, 等. 基于轮轴动应力测试的轮轨力识别与分析[J]. 北京交通大学学报, 2012, 36 (4): 173-177. https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT201204036.htmJIN Xin, JIN Xin-can, GONG Ming, et al. Wheel-rail force identification and analysis based on wheelset dynamic stress testing[J]. Journal of Beijing Jiaotong University, 2012, 36 (4): 173-177. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-BFJT201204036.htm [15] 蒋红光. 高速铁路板式轨道结构-路基动力相互作用及累积沉降研究[D]. 杭州: 浙江大学, 2014.JIANG Hong-guang. Dynamic interaction of slab track structure-subgrade system and accumulative settlement in high-speed railways[D]. Hangzhou: Zhejiang University, 2014. (in Chinese). [16] BIAN Xue-cheng, JIANG Hong-guang, CHEN Yun-min, et al. A full-scale physical model test apparatus for investigating the dynamic performance of the slab track system of a high-speed railway[J]. Journal of Rail and Rapid Transit, 2016, 230 (2): 554-571. doi: 10.1177/0954409714552113 [17] 黄瑛. 高速铁路路基动态响应分析及模型实验装置研制[D]. 长沙: 中南大学, 2009.HUANG Ying. Dynamic response analysis of high-speed railway subgrade and development of model experiment device[D]. Changsha: Central South University, 2009. (in Chinese). [18] 戴林发宝. 高速列车振动作用下水-土-管片耦合及砂土液化分析[D]. 成都: 西南交通大学, 2011.DAI Lin-fa-bao. Study on fluid-particle-lining effect and sand liquefaction under vibration load of high speed railway[D]. Chengdu: Southwest Jiaotong University, 2011. (in Chinese). [19] 陈希成, 蔡成标, 徐鹏. 移动荷载作用下路基上板式轨道动力学特性分析[J]. 铁道建筑, 2007 (11): 94-97. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ200711036.htmCHEN Xi-cheng, CAI Cheng-biao, XU Peng. Analysis on dynamic performance of slab track on subgrade under move loading action[J]. Railway Engineering, 2007 (11): 94-97. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ200711036.htm [20] 周小壮. 无砟轨道路基动态响应特性及室内模型加载方式研究[D]. 长沙: 中南大学, 2011.ZHOU Xiao-zhuang. Study on dynamic response characteristics of ballastless track subgrade and loading mode of indoor model[D]. Changsha: Central South Universty, 2011. (in Chinese). [21] 邵鸣和. 高速列车运行于无砟轨道引起的地面振动数值模拟[D]. 成都: 西南交通大学, 2013.SHAO Ming-he. Numerical simulation of ground vibration induced by high-speed train on non-ballasted railway[D]. Chengdu: Southwest Jiaotong University, 2013. (in Chinese). [22] 王晅, 张家生, 王启云. 无砟轨道路基列车动载激励及动力响应三维数值模拟[J]. 地震工程学报, 2014, 36 (4): 857-867. doi: 10.3969/j.issn.1000-0844.2014.04.0857WANG Xuan, ZHANG Jia-sheng, WANG Qi-yun. Three-dimensional numerical simulation for vehicle dynamic load and dynamic response of ballastless track subgrade[J]. China Earthquake Engineering Journal, 2014, 36 (4): 857-867. (in Chinese). doi: 10.3969/j.issn.1000-0844.2014.04.0857 [23] 朱胜阳, 蔡成标. 温度和列车动荷载作用下双块式无砟轨道道床板损伤特性研究[J]. 中国铁道科学, 2012, 33 (1): 6-12. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201201002.htmZHU Sheng-yang, CAI Cheng-biao. Research on the damage characteristics of double-block ballastless track bed slab under temperature and vehicle dynamic loads[J]. China Railway Science, 2012, 33 (1): 6-12. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-ZGTK201201002.htm [24] 蒋红光, 边学成, 陈云敏, 等. 高速铁路轨道-路基列车移动荷载模拟的全比尺加速加载试验[J]. 土木工程学报, 2015, 48 (9): 85-95. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201509014.htmJIANG Hong-guang, BIAN Xue-cheng, CHEN Yun-min, et al. Full-scale accelerated testing for simulation of train moving loads in track-subgrade system of high-speed railways[J]. China Civil Engineering Journal, 2015, 48 (9): 85-95. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201509014.htm [25] 付昱华. 弹性地基梁按文克尔假设的位移与反力[J]. 铁道标准设计, 1979 (2): 22-24. https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS197902004.htmFU Yu-hua. Displacement and reaction force of elastic foundation beam according to the Winkler hypothesis[J]. Railway Standard Design, 1979 (2): 22-24. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDBS197902004.htm [26] 任娟娟, 田根源, 徐家铎, 等. 客货共线单元板式无砟轨道荷载作用特性与疲劳寿命预测[J]. 铁道学报, 2019, 41 (3): 1-7. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201903016.htmREN Juan-juan, TIAN Gen-yuan, XU Jia-duo, et al. Load effect and fatigue life prediction of prefabricated slab track for mixed passenger and freight railway[J]. Journal of the China Railway Society, 2019, 41 (3): 1-7. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB201903016.htm [27] 梁波, 罗红, 孙常新. 高速铁路振动荷载的模拟研究[J]. 铁道学报, 2006, 28 (4): 89-94. https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200604018.htmLIANG Bo, LUO Hong, SUN Chang-xin. Simulated study on vibration load of high speed railway[J]. Journal of the China Railway Society, 2006, 28 (4): 89-94. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDXB200604018.htm [28] 李潇, 任娟娟, 刘学毅, 等. 客货共线砂浆离缝高度对轨道结构的动力影响[J]. 西南交通大学学报, 2018, 53 (5): 958-965. https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201805012.htmLI Xiao, REN Juan-juan, LIU Xue-yi, et al. Dynamic influence of gap height of CA mortar on track structure under mixed traffic conditions[J]. Journal of Southwest Jiaotong University, 2018, 53 (5): 958-965. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-XNJT201805012.htm [29] 任娟娟, 田根源, 凤翔, 等. 胶垫老化对CRTS Ⅰ型板式无砟轨道结构动力特性的影响[J]. 铁道建筑, 2017 (3): 106-110. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ201703028.htmREN Juan-juan, TIAN Gen-yuan, FENG Xiang, et al. Influence of rubber pad ageing on dynamic characteristics of CRTS Ⅰ slab ballastless track structure[J]. Railway Engineering, 2017 (3): 106-110. (in Chinese). https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ201703028.htm 期刊类型引用(4)
1. 张鲁顺,禹雷,赵磊,刘钰. 列车荷载在双块式无砟轨道中静态传递特征研究. 铁道科学与工程学报. 2021(08): 1951-1959 .  百度学术
百度学术2. 任娟娟,杜威,叶文龙,刘伟,韦臻. 基于PSO-SVM的板式无砟轨道CA砂浆脱空损伤识别. 中南大学学报(自然科学版). 2021(11): 4021-4031 .  百度学术
百度学术3. 曾志平,田春雨,陈卓,王俊东,李世业,吴志鹏. 弹性支承块式无砟轨道冲击振动传递衰减特性试验. 交通运输工程学报. 2020(05): 82-92 .  本站查看
本站查看4. 任娟娟,韦臻,曾学勤,杜威,田晋成,刘伟. CRTSⅠ型双块式无砟轨道轨枕连接面损伤行为分析及识别研究. 中国铁路. 2019(11): 51-59 .  百度学术
百度学术其他类型引用(2)
-






 下载:
下载:





















 下载:
下载:




















 百度学术
百度学术